Measurement Errors Introduction to Study Skills Research Methods

Measurement Errors Introduction to Study Skills & Research Methods (HL 10040) Professor James Betts

Lecture Outline: • Measurement Errors Continued • Types of Errors • Assessment of Error • Introduction to Inferential Statistics • Chi-Squared tests • Assessment Details.

Measurement Errors • Virtually all measurements have errors – i. e. Measured Score = ‘True’ Score Error Therefore inherently linked to SD • Reliability and Measurement Error are not the same, rather Reliability infers an acceptable degree of Measurement Error.

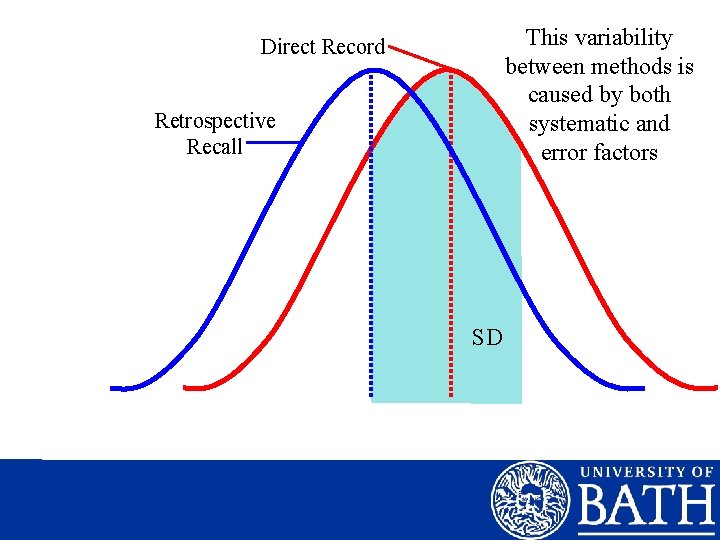
This variability between methods is caused by both systematic and error factors Direct Record Retrospective Recall SD

(SD 2) Systematic Variance Total Variance This total variance can then be ‘partitioned’ Error Variance

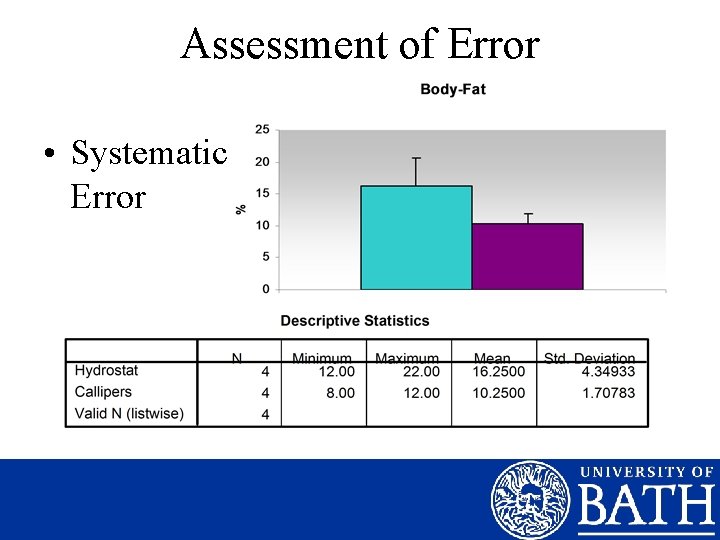
Types of Errors • Systematic Error – Any variable causing a consistent shift in the mean in a given direction e. g. Retrospective diet records tend to omit the snacks between meals • Random Error – The fluctuation of scores due to chance e. g. Innaccurate descriptions of the food consumed

Systematic Error % Body-fat Subject 1 Subject 2 Subject 3 Subject 4 Skin-Fold Callipers 10 12 8 11 Hydrostatic Weighing 17 22 14 12

Random Error % Body-fat Subject 1 Subject 2 Subject 3 Subject 4 Skin-Fold Callipers 14 18 10 9 Hydrostatic Weighing 11 15 21 17

Assessment of Error • Systematic Error

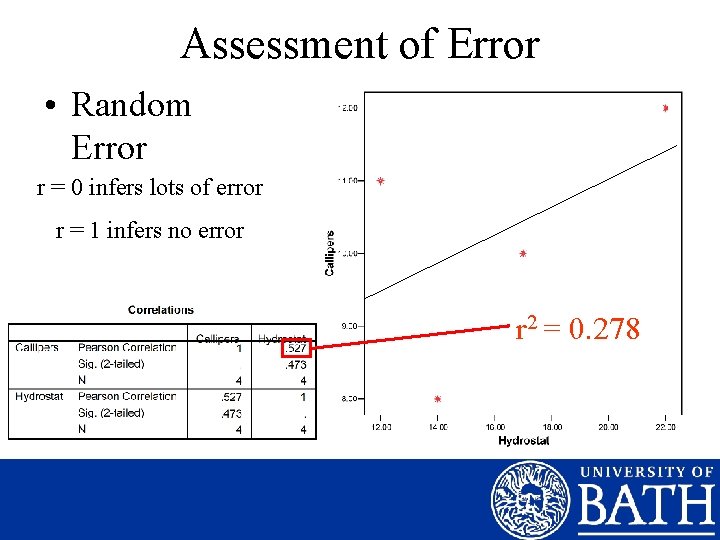
Assessment of Error • Random Error r = 0 infers lots of error r = 1 infers no error r 2 = 0. 278

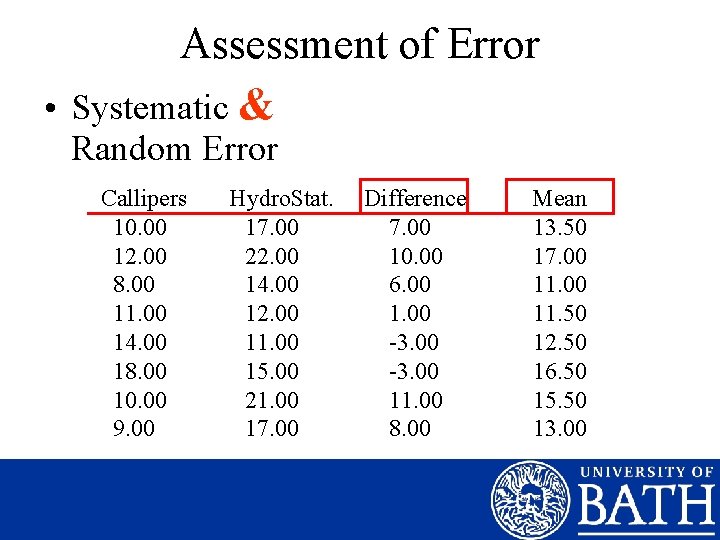
Assessment of Error • Systematic & Random Error Callipers 10. 00 12. 00 8. 00 11. 00 14. 00 18. 00 10. 00 9. 00 Hydro. Stat. 17. 00 22. 00 14. 00 12. 00 11. 00 15. 00 21. 00 17. 00 Difference 7. 00 10. 00 6. 00 1. 00 -3. 00 11. 00 8. 00 Mean 13. 50 17. 00 11. 50 12. 50 16. 50 15. 50 13. 00

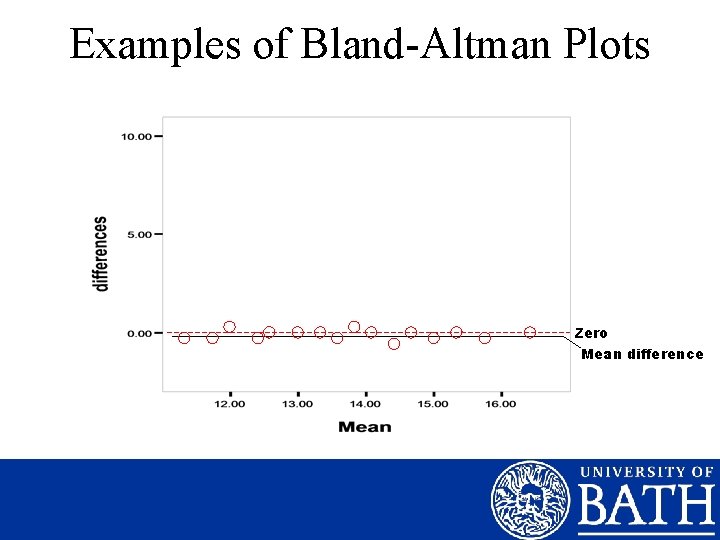
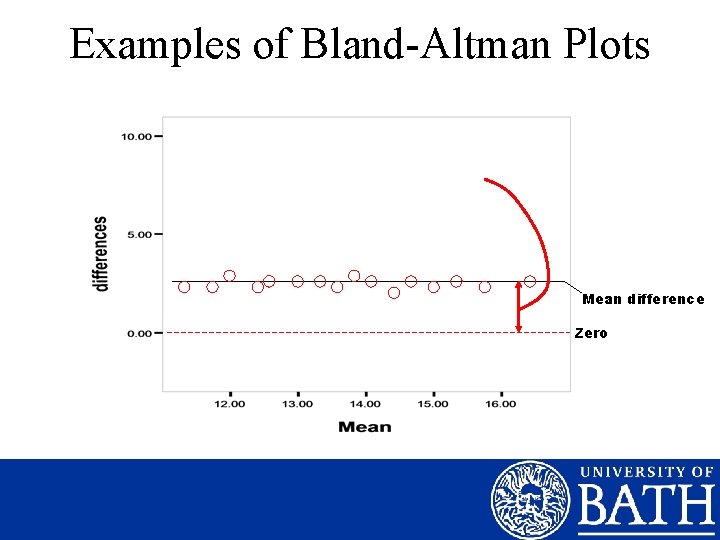
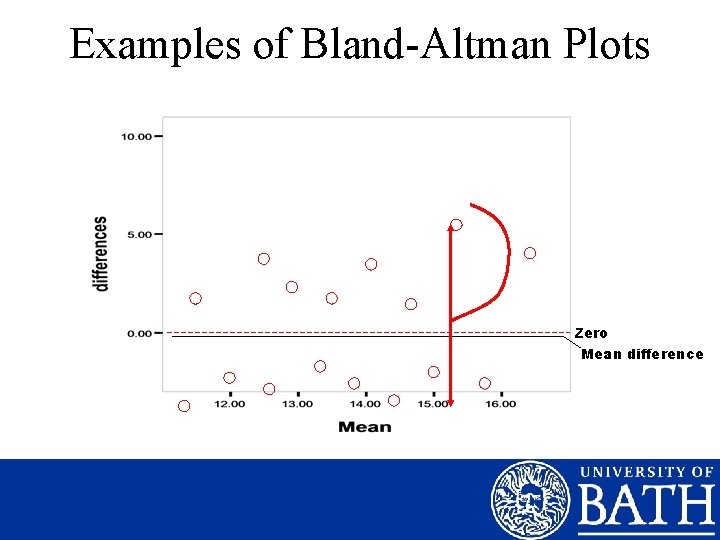
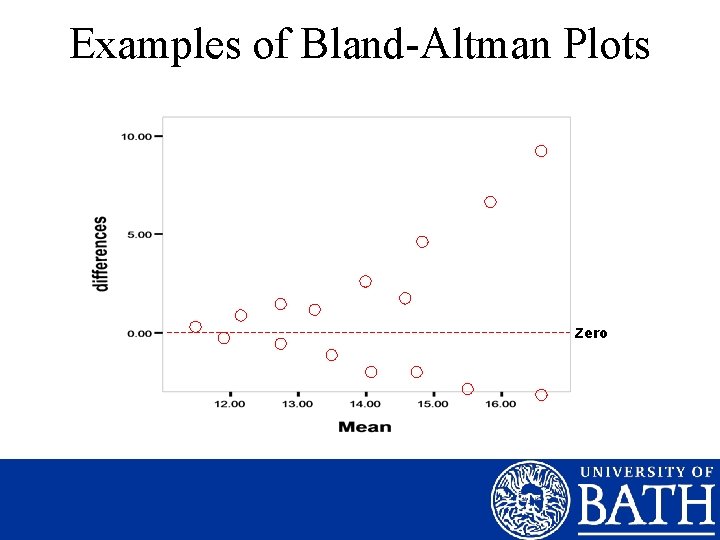
Assessment of Error • Systematic & Random Error The “Bland-Altman” Plot 3 points of visual assessment: -Systematic Error: are points evenly distributed about the zero line? -Random Error: do points deviate greatly from the mean line? -Nature of error: is the error consistent left-right?

Examples of Bland-Altman Plots Zero Mean difference

Examples of Bland-Altman Plots Mean difference Zero

Examples of Bland-Altman Plots Zero Mean difference

Examples of Bland-Altman Plots Mean difference Zero

Examples of Bland-Altman Plots Zero

Why is Error Important • Measurement Error is clearly of importance when evaluating the agreement between two measurement tools • A consideration of error is also relevant when attempting to establish intervention effects/treatment differences i. e. where some of the variance between trials is due to the independent variable. . .

Dependent Variable Independent Variable Total Variance between trial 1 & trial 2 Extraneous/ Confounding (Error) Variables Primary Variance Systematic Variance Error Variance So researchers strive to increase the proportion of variance due to IV.

Smallest Worthwhile Effect It would appear that even a small amount of primary variance from an ergogenic aid would guarantee victory to either competitor… …however, the error variance is such that a re-run could produce entirely different results…

Dependent Variable Systematic Variance Extraneous/ Confounding (Error) Variables Total Variance between trial 1 & trial 2 Error Variance So researchers strive to increase the proportion of variance due to IV.

Scientific Reasoning (Logic) Confirmation of a theory from your own observations General Theory Deductive Reasoning Inductive Reasoning Specific Observation Formation of a theory grounded in your own observations p-values give the probability of seeing this evidence assuming this general rule is true

Introduction to Inferential Statistics • Before our next lecture you will be conducting some inferential statistics in your lab classes… • All you need to be aware of at this stage is that the ‘p -value’ represents the probability of the observed variance occurring if the null hypothesis is true i. e. p = 0. 05 infers a 5 % probability of making your observation if in fact the IV has no effect n. b. this DOES NOT mean that you will find this result in 95/100 test-retests or that your false positive rate is 5 %

Quantitative Analysis of Nominal Data • Recall that nominal data infers that variables are dichotomous, i. e. belong to distinct categories e. g. Athlete/Non-Athlete, Male/Female, etc. • We know that such qualitative data can be coded quantitatively to allow a more objective analysis • Nominal data does not require any consideration of normality and is analysed used a Chi 2 test.

The Chi-Squared Test • Goodness of fit χ2 test – A comparison of your observed frequency counts against what would be expected according to the null hypothesis i. e. null hypothesis infers equal dispersion (50: 50) • Contingency χ2 test – A comparison of two observed frequency counts

Goodness of fit χ2 test • Is a leisure centre used more by males than by females? – n =150 Observed Frequency Expected Frequency Male 62 75 Female 88 75

Goodness of fit χ2 test SPSS Output p-value AKA significance level

Contingency χ2 test • Are elite athletes more likely to take nutritional supplements than non-athletes – n =60 Do take supplements Do not take supplements Athletes 18 12 Non-athletes 11 19

Contingency χ2 test SPSS Output

Assumptions for Chi-Squared • Although ND not required… • Cells in the table should all be independent i. e. one person could have visited the leisure centre twice • 80 % of the cells must have expected frequencies greater than 5 and all must be above 1 i. e. the more categories available, the more subjects needed • Cannot use percentages i. e. a 15: 45 split cannot be expressed as 25%: 75%

Selected Reading • I know error and variance can be confusing topics, try these: • Atkinson, G. and A. M. Nevill. Statistical methods for assessing measurement error (Reliability) in variables relevant to sports medicine. Sports Medicine. 26: 217 -238, 1998. • Hopkins, W. G. et al. Design and analysis of research on sport performance enhancement. Med. Sci. Sport and Exerc. 31: 472 -485, 1999. • Hopkins, W. G. et al. Reliability of power in physical performance tests. Sports Medicine. 31: 211 -234, 2001. • Atkinson, G. , ''What is thing called measurement error? '' , in Kinanthropometry VIII: Proceedings of the 8 th International Conference of the International Society for the Advancement of Kinanthropometry (ISAK) , Reilly, T. and Marfell-Jones, M. (Eds. ), Taylor and Francis, London , 2003.

Coursework (60% overall grade) • Your coursework will require you to address ONE of the following research scenarios: – 1) Effect of Plyometric Training on Vertical Jump – 2) Effect of Ice Baths on Recovery of Strength – 3) Effect of Diet on the Incidence of Muscle Injury – 4) Effect of Footwear on Sprint Acceleration – 5) Effect of PMR on Competitive Anxiety.

Coursework Outline • For the selected scenario you will need to: – Perform a literature search in order to provide a comprehensive introduction to the research area – Identify the variables of interest and evaluate the research design which was adopted – Formulate and state appropriate hypotheses – Summarise descriptive statistics in an appropriate and well presented manner…

Coursework Outline • Cont’d… – Select the most appropriate statistical test with justification for your decision – Transfer the output of your inferential statistics into your word document – Interpret your results and discuss the validity and reliability of the study – Draw a meaningful conclusion (state whether hypotheses are accepted or rejected).

Coursework Details (see unit outline) • 1000 words (2000 absolute maximum) • Any supporting SPSS data/outputs to be appended • To be submitted on Thursday 12 th December Assessment Weighting Evaluation & Analysis (30 %) Reading & Research (20 %) Communication & Presentation (20 %) Knowledge (30 %)

Coursework Details • All information relating to your coursework (including the relevant data files) are accessible via the unit web page: www. bath. ac. uk/~jb 335/Y 1%20 Research%20 Skills%20(FH 10040). html Web address also referenced on shared area

Mid-Term Test (40% overall grade) • NEXT WEEK • This test will involve short answer questions covering all the information covered so far • Mostly knowledge recall but will require understanding and possibly some calculations • Duration = 50 min So…

Mid-Term Test (40% overall grade) • Surnames: A-K – Arrive promptly at 11. 10 am for start of test at 11. 15 am – Exit in silence afterwards • Surnames: L-Z – Arrive promptly at 12. 10 am for start of test at 12. 15 am – Exit however you like!

J. Betts@bath. ac. uk