Measurement and Uncertainty Tutorial for Physics 11011120 Labs

Measurement and Uncertainty Tutorial for Physics 1101/1120 Labs

The material in this tutorial is based on the following two reference books and tailored for the use in our physics labs according to the objectives of the specific courses and also the particular equipment we use.

This material is also contained in your 1101/1120 lab manual for your reference.

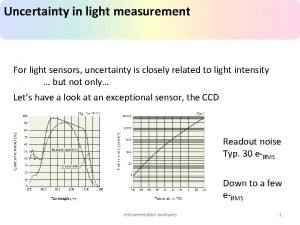
1 Measurement and Uncertainty Measurement is at the heart of experimental science. Regardless of how carefully a measurement is taken, there is always some uncertainty. In this course, you will be required to record every measurement you take with an uncertainty to reflect this: estimated value ± uncertainty For example: Length of block, L = 21. 4 ± 0. 2 cm An uncertainty gives a range of values that you are reasonably certain the measurement falls into (in this case, 21. 2 to 21. 6 cm). The uncertainty is often determined by the instrument itself. Figure 1 will be used to illustrate this.

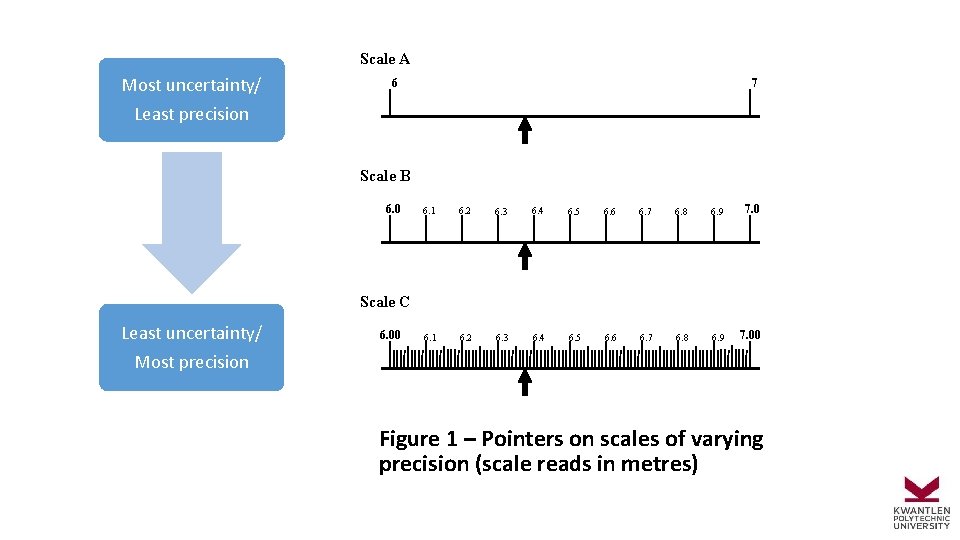
Scale A Most uncertainty/ Least precision 6 7 Scale B 6. 0 6. 1 6. 2 6. 3 6. 4 6. 5 6. 6 6. 7 6. 8 6. 9 7. 00 Scale C Least uncertainty/ Most precision 6. 00 Figure 1 – Pointers on scales of varying precision (scale reads in metres)

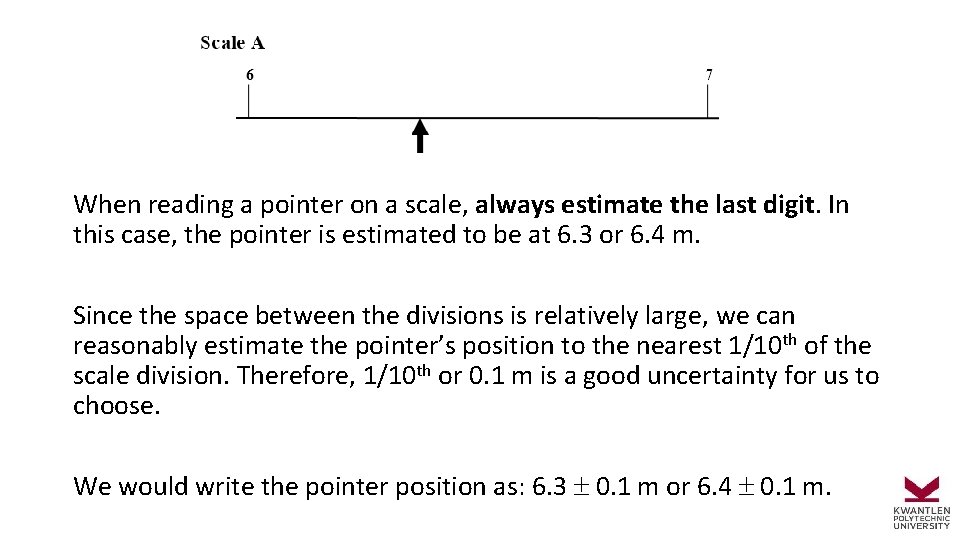
When reading a pointer on a scale, always estimate the last digit. In this case, the pointer is estimated to be at 6. 3 or 6. 4 m. Since the space between the divisions is relatively large, we can reasonably estimate the pointer’s position to the nearest 1/10 th of the scale division. Therefore, 1/10 th or 0. 1 m is a good uncertainty for us to choose. We would write the pointer position as: 6. 3 0. 1 m or 6. 4 0. 1 m.

On Scale B, there are more divisions. For this reason, we can read the pointer to a greater precision. The best estimate of the pointer position in this case might be 6. 38 m, where “ 8” is an estimated digit (another person might estimate that digit differently than you). Because the division spacing is still large, we can again use 1/10 th of the smallest division as our uncertainty: 6. 38 0. 01 m. Note that a person with better or poorer eyesight than average is justified in making their uncertainty smaller or larger than this value.

On Scale C, our best estimate of the value might be 6. 375 m, where the “ 5” is estimated. However, the division spacing on Scale C is so small that most people could no longer estimate their final digit accurately to 1/10 th of the smallest division. In this case we might then use the more realistic uncertainty ½ of the smallest division as our uncertainty, i. e. , 0. 005 m. The value would be written as: 6. 375 0. 005 m.

For most of the instruments in our lab, the calibration of the scales is quite fine, so that it is usually safe to use ½ the smallest scale division for the uncertainty of reading a pointer on a scale. Remember to estimate the last digit of your reading. Note: If the position is directly on a division and not between two divisions, then your last digit estimated should be zero to indicate that you are estimating the position to be directly on that division, as opposed to a little bit off of it. Here are some examples for you to consider.

Hooke’s Law Apparatus (in cm) First, estimate the position of the pointer on the scale. You might choose 9. 19 cm. Next, estimate the uncertainty to be ½ the smallest scale division: ± 0. 05 cm. Therefore, a correctly expressed measurement would be: 9. 19 ± 0. 05 cm.

Thermometer (in degrees Celsius) First, estimate the position of the alcohol in thermometer (remember to always estimate the last digit of the reading, even if it’s a zero). You might choose 27. 0 ˚C. Next, estimate the uncertainty to be ½ the smallest scale division: ± 0. 5 ˚C. Therefore, the correctly expressed measurement would be: 27. 0 ± 0. 5 ˚C.

Protractor (in °) Using the top scale on the protractor, select the best way to express this measurement? 146. 55 ± 0. 05 ° 146. 5 ± 0. 5 ° 146. 50 ± 0. 5 ° 146. 5 ± 0. 05 °

Voltmeter (in V) Using the top scale on the voltmeter readout, which of the following would be an acceptable measurement? Note that there were 2 correct answers in this case… pick either one! 8. 75 ± 0. 5 V 8. 7 ± 0. 25 V 8. 7 ± 0. 5 V 8. 6 ± 0. 25 V

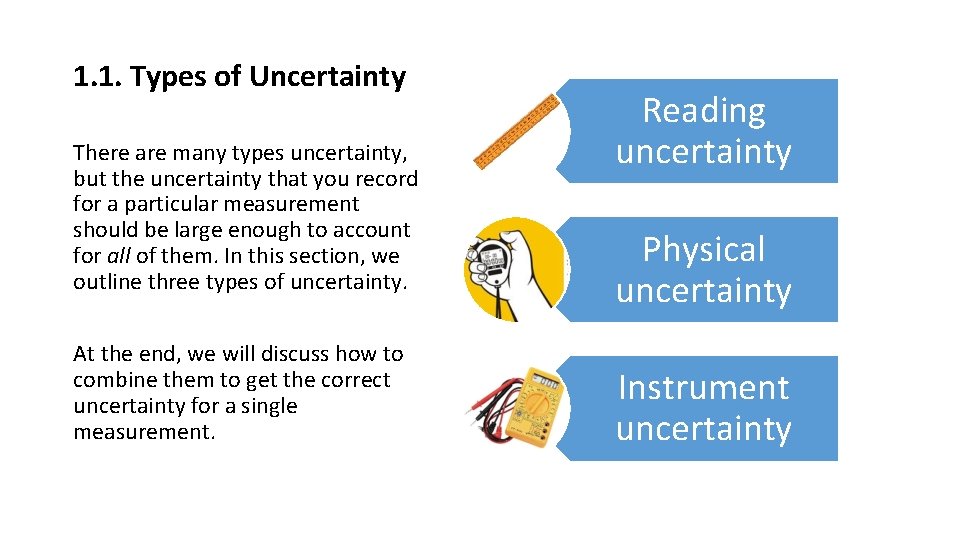
1. 1. Types of Uncertainty There are many types uncertainty, but the uncertainty that you record for a particular measurement should be large enough to account for all of them. In this section, we outline three types of uncertainty. At the end, we will discuss how to combine them to get the correct uncertainty for a single measurement. Reading uncertainty Physical uncertainty Instrument uncertainty

1. 1. 1 Reading Uncertainty The reading uncertainty is set by how accurately you can read a value off a scale. All of the uncertainties discussed in the previous section, for Scales A, B and C of Figure 1, Hooke’s law apparatus scale, thermometer, protractor and voltmeter were all reading uncertainties. Reading uncertainty is determined both by how precise the measuring device is, and how accurately you can read a measurement off it. That includes such factors as the pointer being shaky or thick, as well as the spacing of the scale increments and how good your eyesight is. Note: The uncertainty value you choose is a judgment call. However, there is an acceptable range of values and outside this range, the uncertainty is not acceptable. What’s important is that you can reasonably justify the uncertainty value you choose (recording this justification is common practice).

Angle with Horizontal (in °) This instrument is used to find the angle with horizontal. Which of the following would be acceptable measurements? 32. 5 ± 0. 01 ° 32. 5 ± 0. 5 ° 32. 5 ± 1 °

Ruler Measurements When you take a measurement of length of something well-defined (like a block of wood with sharp edges) with a ruler, keep in mind that you have two reading uncertainties. One of them comes from reading the length of the object, and the other comes from lining up the edge of the object with zero on your ruler. Because of this, when measuring a length with a ruler, it is appropriate to make your uncertainty twice as big: e. g. , 2 (1/2 th the smallest division) = 2 (0. 05 cm) = 0. 1 cm Therefore, a good measurement would be 12. 9 ± 0. 1 cm.

1. 1. 2 Physical Uncertainty Sometimes the quantity you are measuring has an intrinsic uncertainty that is larger than the reading uncertainty of the device you are using to measure it. For example, if you try to measure the length of a pencil, the roundness of the eraser and the difficulty in lining up the tip with the ruler is where most of your uncertainty comes from – not the precision of the ruler. Your reading uncertainty might be ± 0. 05 or ± 0. 1 cm, but the pencil has a poorly defined ends, so the physical uncertainty is larger, maybe 0. 2 cm. Therefore, L = 16. 8 ± 0. 25 cm or even L = 16. 8 ± 0. 3 cm.

Another example would be a measurement of how long something takes using a stopwatch (e. g. , 10 oscillations of the Hooke’s Law apparatus shown here). There is no reading uncertainty if the stopwatch is digital, but there is a physical uncertainty to take into account, namely your reaction time. The average human reaction time is about 0. 15 s. Therefore this measurement might be expressed as t = 4. 91 ± 0. 15 s.

1. 1. 3 Instrument Uncertainty The instrument you are taking a measurement with can contain a built-in uncertainty that has nothing to do with your ability to read the device. For example, a device with a digital display has no reading uncertainty (since you simply record all the digits displayed), but you don’t know what the uncertainty of that device is until you read the manufacturer’s specifications. In this course, whenever you use an instrument with a digital display, the instrument uncertainty will be provided in the apparatus section of the lab manual. For example, Therefore, the width of the block measurement shown here would be: w = 18. 71 ± 0. 03 mm

Digital Calipers (in mm) Which of the following would be the correct way to express the measurement? 21. 09 ± 0. 01 mm 21. 09 ± 0. 03 mm 21. 09 ± 0. 05 mm 21. 09 ± 0. 1 mm

Analogue versus Digital Displays Please note that a device with a digital display is not necessarily more precise than a device with a pointer on a scale (i. e. , an analogue display). Digital displays are easy to read, but the device attached to them is not necessarily of any higher quality. For example, this analogue galvanometer can read to a much higher precision than this digital meter. In fact, you will often see the highest quality instruments with analogue displays.

1. 2. 4 How to Determine Your Total Uncertainty Choosing the correct uncertainty on a single measurement is a judgment call. You want to choose a value large enough to take into account all of the sources of uncertainty present, but small enough to reasonably represent the precision of your measurement. While there is room for judgment and variation between you and others, there is also an acceptable range and outside of that, it is not a good estimation. You will be asked to justify your choices. In general, add up all of the uncertainties present in any particular measurement. Note: you may have only one type, or you may have more. Reading uncertainty Physical uncertainty Instrument uncertainty Total uncertainty

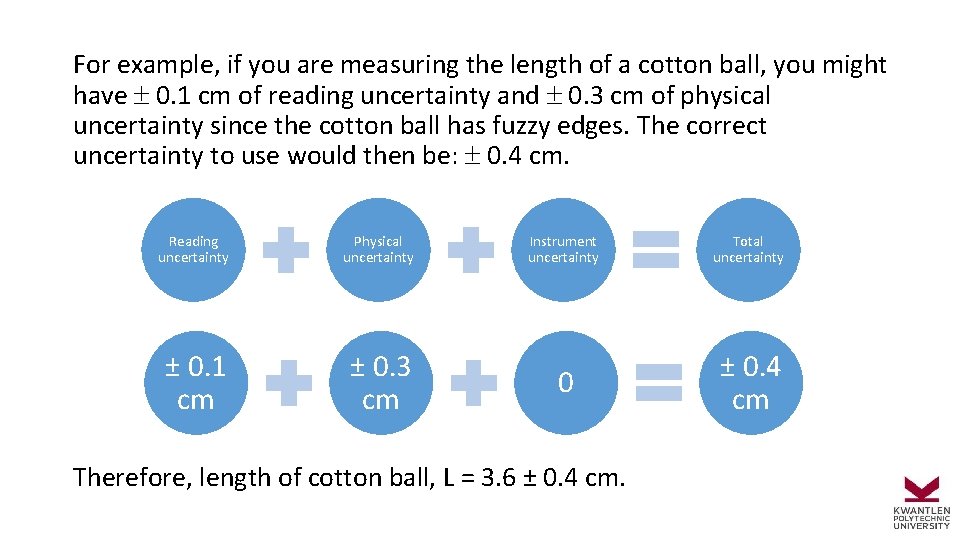
For example, if you are measuring the length of a cotton ball, you might have 0. 1 cm of reading uncertainty and 0. 3 cm of physical uncertainty since the cotton ball has fuzzy edges. The correct uncertainty to use would then be: 0. 4 cm. Reading uncertainty ± 0. 1 cm Physical uncertainty ± 0. 3 cm Instrument uncertainty 0 Therefore, length of cotton ball, L = 3. 6 ± 0. 4 cm. Total uncertainty ± 0. 4 cm

This next example brings up one final point on this topic. Let’s say you are measuring the time it takes for a complete period of a pendulum with a stopwatch. You have the physical uncertainty of reaction time (± 0. 15 s) and you may also have an instrument uncertainty given by the manufacturer of the stopwatch, say ± 0. 001 s. Reading uncertainty Physical uncertainty Instrument uncertainty Total uncertainty 0 ± 0. 15 s ± 0. 001 s ± 0. 151 s Notice how the instrument uncertainty is very small compared to the physical uncertainty. In cases like this, it’s common to disregard tiny uncertainties that are overwhelmed by the other(s). Therefore, the uncertainty of the time is given simply as ± 0. 15 s.

Let’s say you are measuring the diameter of this lens with this ruler. Which of the following would be acceptable measurements? Note: 2 are correct; pick either one 7. 8 ± 0. 05 cm 7. 8 ± 0. 1 cm 7. 8 ± 0. 2 cm 7. 8 ± 0. 3 cm 7. 8 ± 0. 4 cm

We will look at each operation separately first and then combine them together later. The formulas are summarized in section 3 (pp. 9 -10) of your 1101/1120 lab manual for future reference.

Note: This may be applied to any number of terms being added or subtracted (we are just showing 3 here to give you the idea). Also note: subtraction is done in the exact same way as addition.

Note: This may be applied to any number of terms being multiplied or divided (we are just showing 3 here to give you the idea). Also note: division is done in the exact same way as multiplication.

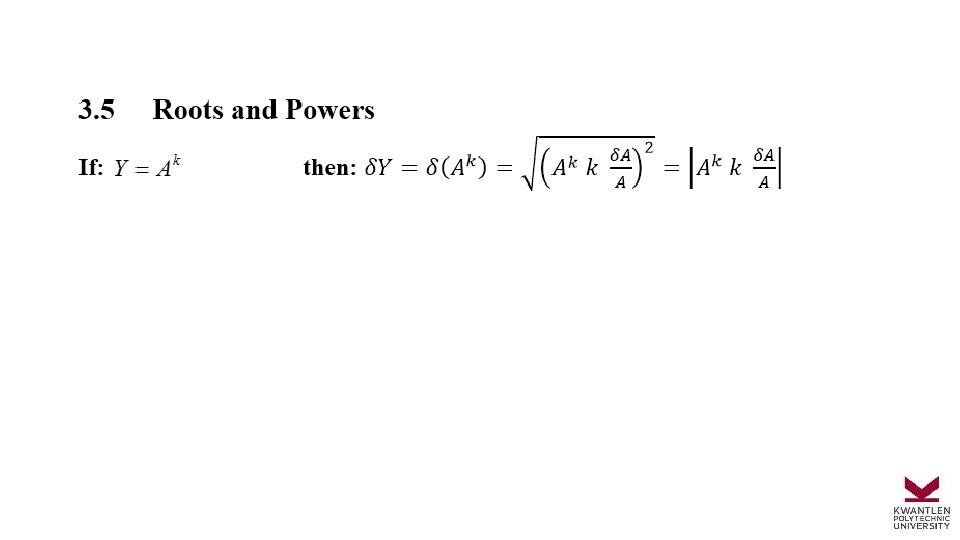
There are many other equations you will use from time to time, but you should be able to figure these out when the time comes. Here a few of them:

One more that will be useful to consider is the uncertainty of an average of many values:

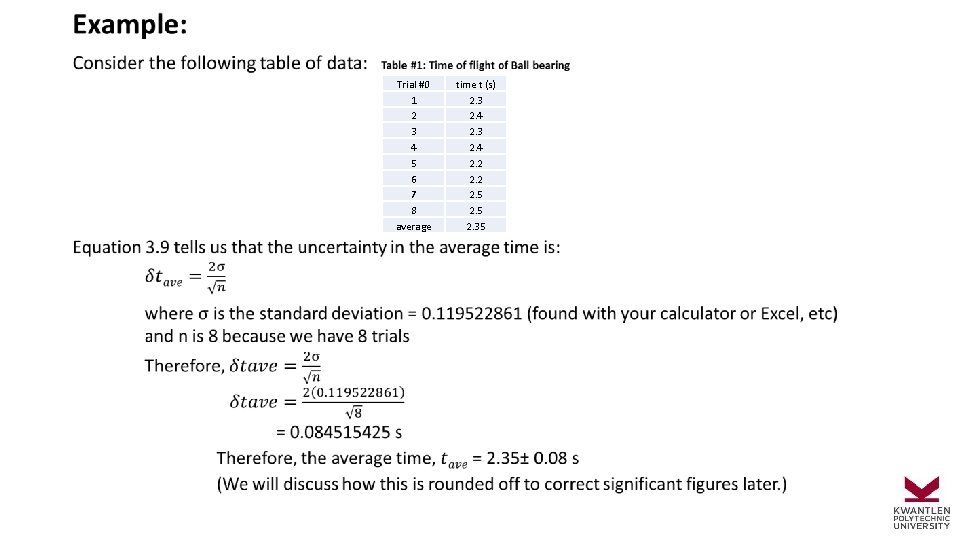
Trial #0 1 2 3 4 5 6 7 8 average time t (s) 2. 3 2. 4 2. 2 2. 5 2. 35

For the following set of data, Table #1: Force Readings for Pulling a Block from Rest Trial # Force of Static Friction Ff (N) 1 3. 1 ± 0. 1 2 3. 6 ± 0. 1 3 3. 1 ± 0. 1 4 3. 2 ± 0. 1 5 3. 1 ± 0. 1 6 3. 3 ± 0. 1 Average 3. 23333 The standard deviation of 3. 1, 3. 6, 3. 1, 3. 2, 3. 1 and 3. 3 is 0. 1966384 (normally, you will have to figure this out, but we’ll give it here this time). Which of the following is correct?

Go back 2 screens and use the data given to find the uncertainty of Fnet. You will need to use some scrap paper and/or your calculator. Which of the following is correct? Note: there is some rounding off in the final value (but not before!). This will be our next (and last) topic of this tutorial.

Let’s say you have done all of your calculations and have these results: I=0. 02374889534 A δI=0. 00054989541 A Which of the following is the correct rounding for δI?

Let’s say you have done all of your calculations and have these results: I=0. 02374889534 A δI=0. 00014989541 A Which of the following is the correct rounding for δI?

Let’s say you have done all of your calculations and have these results: I=0. 02374889534 A δI=0. 00054989541 A Which of the following is the correct rounding for I?

Given: V = 31. 654782967 cm/s δv = 0. 4167589 cm/s Which of the following is correct?

Given: KE = 325. 6729555 J δKE = 0. 02567456 J Which of the following is correct?