Measurement and Certainty Or I weigh 152 3746382

Measurement and Certainty Or, “I weigh 152. 3746382 pounds”

SI (Système international d’unités) • International system of units (metric system) based on multiples of 10. • Examples: kilograms, liters, meters

standard • Exact, agreed-upon quantity used for comparison

SI Base Units • Seven measurement units from which all other units can be derived: • Distance: meters (m) Learn • Time: seconds (s) • Mass: kilograms (kg) • Temperature: Kelvin (K) • Number of particles: moles (mol) • Electric current: Amperes (A) • Brightness of light: candellas (cd) NOW Learn LATER

Derived units • Units that come from (derived from) a mathematical operation of two or more standard units • Example: (speed) m/s, (density) g/L • 1 Pa = 1 N/m 2 = 1 kg/ms 2

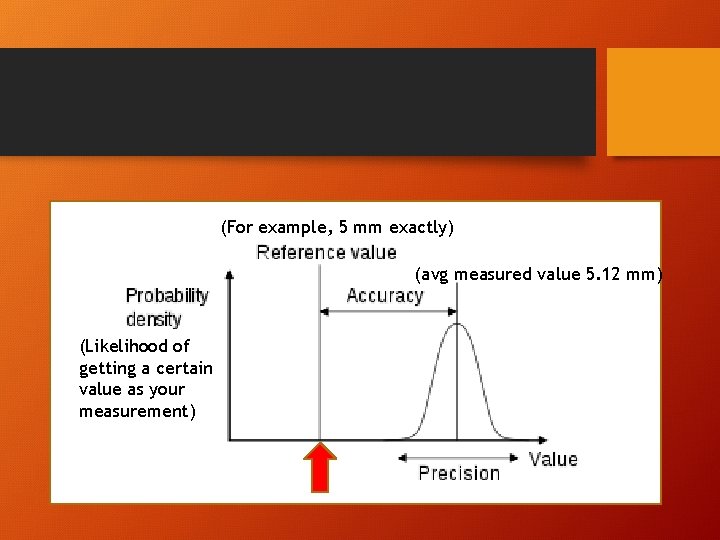
Error in measurement • A measurement is an assignment of a value to a characteristic of something. • When a measurement is made, uncertainty is always involved • There are two limitations of a measuring system: • Accuracy • Precision

accuracy • degree of closeness of measurements of a quantity to that quantity's true value • Measurement instruments need to be calibrated properly to achieve best accuracy

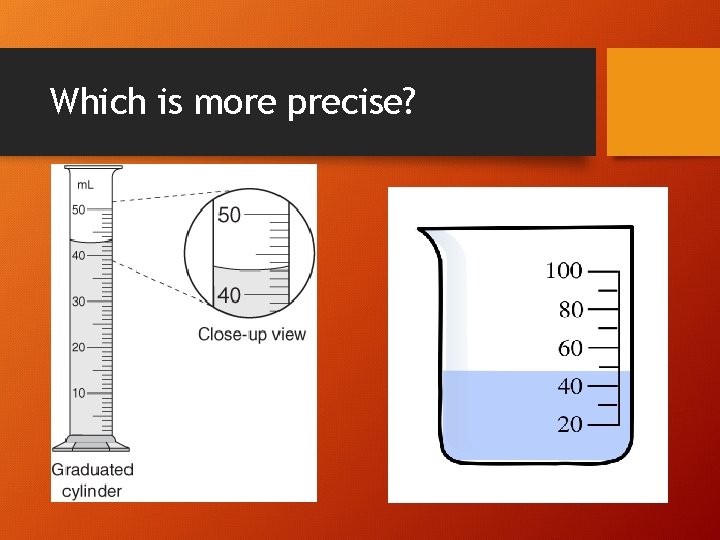
precision • How similar/close repeated measurements are to each other. • (Reproducibility or variation of measurements)

(For example, 5 mm exactly) (avg measured value 5. 12 mm) (Likelihood of getting a certain value as your measurement)

Illustration: accuracy vs. precision

Which is more precise?

Significant figures • The digits in a measurement about which we are confident, plus one estimated digit. • Confidence of our measurement (the number of sig figs) is determined by the precision of our instrument

Sig Figs rules (assumptions) • The following rules assume that a measurement was taken and recorded properly…

Sig Figs rules (assumptions) 1. Any non-zero digit is considered to be significant. 2. Any zero between significant digits is considered significant. 3. Only final zeros after a decimal are considered significant. All other zeros, unless indicated are not significant and are considered placeholders.

3 b. A line placed over a zero may be used to indicate that it is significant: 0

Practice • 305 m • 3050 s • 30500 km • 3. 50°C • 0. 00305 m • 0. 003050 kg • 30. 00500 mm

Multiplying/Dividing • The product or quotient of two numbers is rounded to the same number of sig. figs. as the number with the least number of sig. figs. • 46. 2 X 11 = 508. 2 • 510

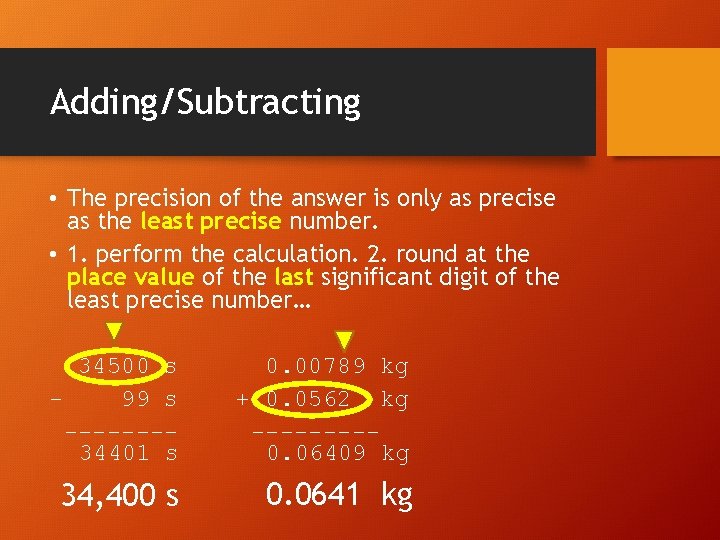
Adding/Subtracting • The precision of the answer is only as precise as the least precise number. • 1. perform the calculation. 2. round at the place value of the last significant digit of the least precise number… 34500 s 99 s -------34401 s 0. 00789 kg + 0. 0562 kg ----0. 06409 kg 34, 400 s 0. 0641 kg

Numbers that are not measurements • Some numbers, like the number of people counted in a room, or the value for π, are exact and therefore have infinite significant figures. • These numbers DO NOT affect the number of significant figures in a calculation.

Making measurements with Instruments • Recording significant figures assumes that the instrument is calibrated, it is as precise as advertised, and you are reading it correctly. • 2 steps: • Record the digits for which you are certain • Estimate the last digit to the best of your ability (it can be 0 -9) • KEEP YOUR EYES LEVEL WITH THE MARK!

Reading liquids in graduated cylinders • For reading volumes of water, read at the bottom of the meniscus (curve), at eye level.

Scientific notation background… • Really big (and small) numbers are hard to write, and are hard to use in calculations! • (example: world population estimated to be 7, 525, 986, 931 people (on Aug 17, 2017 in the am) • Most big or very small numbers are measurements with uncertainty • (we are confident that the world has 7. 53 billion people)

• Scientific notation is a solution that will make your life as a scientist EASIER!!!

Scientific notation • A way to write very small or very large numbers • Expressed in the form m x 10 n where n is any integer • m is a number with digits only in the ones place value and lower (examples: 5, 3. 2, 9. 005, but not 50)

Base 10 exponents • 10 n= a 1 with n zeros behind it • 103 = 1, 000 (thousand) • 106 = 1, 000 (million) • 109 = 1, 000 (billion) • 100 = 1

Negative exponents •

Multiplying base 10 exponents •

Expanding from scientific notation • If the exponent is positive, move the decimal over to the right n times. • 2. 31 x 103 = • If the exponent is negative, move the decimal over to the left n times • 4. 578 x 10 -4=

Converting to scientific notation • 200 s • What if the second zero was actually a sig fig? Express in scientific notation! • Go backwards. • 2. 0 x 102 s

Practice (answer in s. n. with sig figs) •