Measurement Accuracy vs Precision Percent Error Significant Figures

Measurement • • Accuracy vs Precision Percent Error Significant Figures Scientific Notation Temperature Conversions Dimensional Analysis Conversion Factors SI Conversions

Number vs. Quantity • Quantity = number + unit UNITS MATTER!!

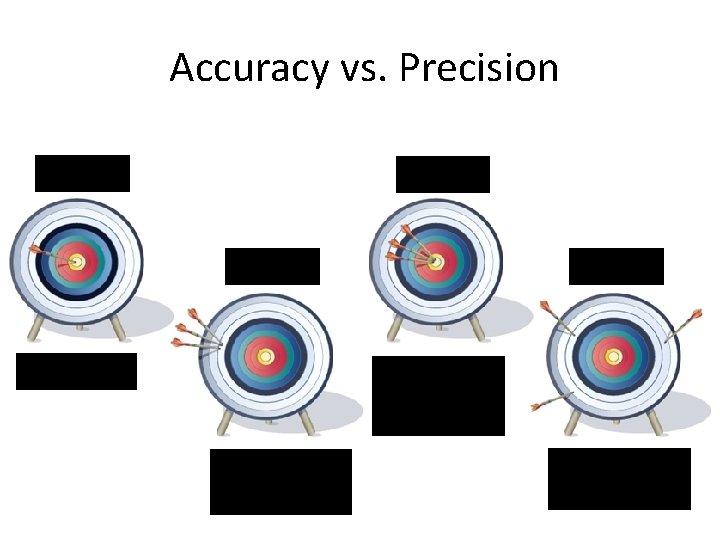
Accuracy vs. Precision • Accuracy - how close a measurement is to the accepted value • Precision - how close a series of measurements are to each other ACCURATE = CORRECT PRECISE = CONSISTENT

Accuracy vs. Precision

Percent Error • Indicates accuracy of a measurement your value given value

Percent Error • A student determines the density of a substance to be 1. 40 g/m. L. Find the % error if the accepted value of the density is 1. 36 g/m. L. % error = 2. 94 %

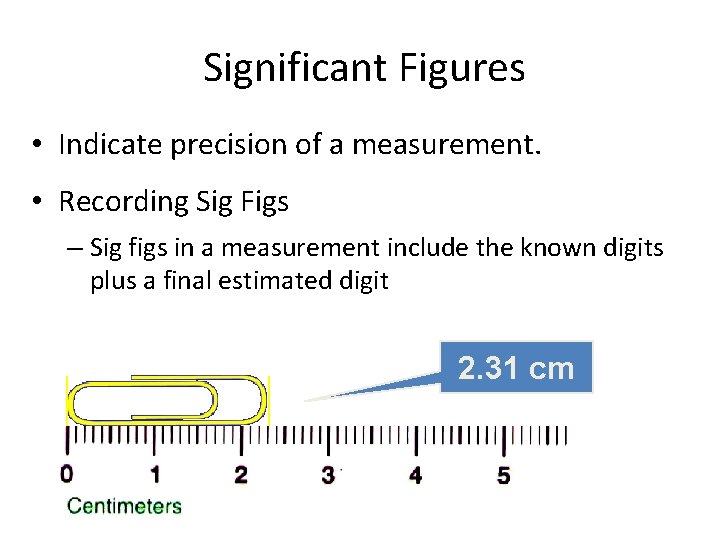
Significant Figures • Indicate precision of a measurement. • Recording Sig Figs – Sig figs in a measurement include the known digits plus a final estimated digit 2. 31 cm

Significant Figures • Counting Sig Figs – Digits from 1 -9 are always significant 739 – Zeros between two other sig figs are always significant 5085 – One or more additional zeros to the right of both the decimal place and another sig digit are significant 2. 60 – Count all numbers EXCEPT: • Leading zeros -- 0. 0025 • Trailing zeros without a decimal point -- 2, 500

Significant Figures Counting Sig Fig Examples 1. 23. 50 4 sig figs 2. 402 3 sig figs 3. 5, 280 3 sig figs 4. 0. 080 2 sig figs

Significant Figures • Calculating with Sig Figs – Multiply/Divide - The # with the fewest sig figs determines the # of sig figs in the answer (13. 91 g/cm 3)(23. 3 cm 3) = 324. 103 g 4 SF 324 g

Significant Figures • Calculating with Sig Figs (con’t) – Add/Subtract - The # with the lowest decimal value determines the place of the last sig fig in the answer 3. 75 m. L + 4. 1 m. L 7. 85 m. L 7. 9 m. L

Significant Figures • Calculating with Sig Figs (con’t) – Exact Numbers do not limit the # of sig figs in the answer • Counting numbers: 12 students • Exact conversions: 1 m = 100 cm • “ 1” in any conversion: 1 in = 2. 54 cm

Significant Figures Practice Problems 5. (15. 30 g) ÷ (6. 4 m. L) 6. 18. 9 g - 0. 84 g 18. 1 g 2. 4 g/ml

Scientific Notation • A way to express any number as a number between 1 and 10 (coefficient) multiplied by 10 raised to a power (exponent) • Number of carbon atoms in the Hope diamond • 460, 000, 000, 000 atoms • 4. 6 x 1023 atoms coefficient exponent

Scientific Notation 65, 000 kg 6. 5 × 104 kg • Converting into Sci. Notation: – Move decimal until there’s 1 digit to its left. Places moved = exponent – Large # (>1) positive exponent Small # (<1) negative exponent – Only include sig figs – all of them!

Scientific Notation Practice Problems 7. 2, 400, 000 g 8. 0. 00256 kg 9. 7. 0 10 -5 km 10. 6. 2 4 10 mm

Scientific Notation • Calculating with Sci. Notation (5. 44 × 107 g) ÷ (8. 1 × 104 mol) = Type on your calculator: 5. 44 EXP EE 7 ÷ 8. 1 EXP EE 4 EXE ENTER = 671. 6049383 = 670 g/mol = 6. 7 × 102 g/mol

Scientific Notation Practice Problems 11. (4 x 102 cm) x (1 x 108 cm) 12. (2. 1 x 10 -4 kg) x (3. 3 x 102 kg) 13. (6. 25 x 102) ÷ (5. 5 x 108) 14. (8. 15 x 104) ÷ (4. 39 x 101) 15. (6. 02 x 1023) ÷ (1. 201 x 101)

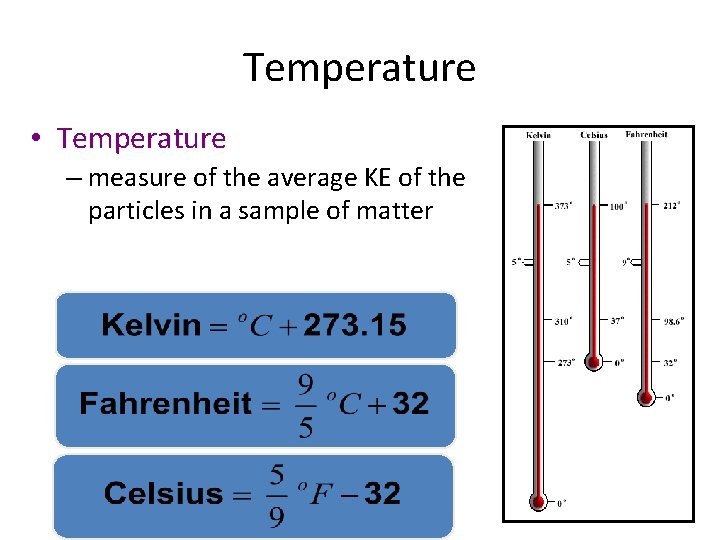
Temperature • Temperature – measure of the average KE of the particles in a sample of matter

Temperature • Convert these temperatures: 1) 25 o. C = _______K 2) -15 o. F = _______ K 3) 315 K = _______ o. C 4) 288 K = _______ o. F

Dimensional Analysis • Dimensional Analysis is also called Unit Analysis and is a great way to solve problems in chemistry (or any time).

Dimensional Analysis • Dimensional Analysis – A tool often used in science for converting units within a measurement system • Conversion Factor – A numerical factor by which a quantity expressed in one system of units may be converted to another system

Dimensional Analysis Problem-Solving Steps 1. Analyze 2. Plan 3. Compute 4. Evaluate

Dimensional Analysis • The “Factor-Label” Method – Units, or “labels” are canceled, or “factored” out

Dimensional Analysis • Steps to solving problems: 1. Identify starting & ending units. 2. Line up conversion factors so units cancel. 3. Multiply all top numbers & divide by each bottom number. 4. Check units & answer.

Conversion Factors Fractions in which the numerator and denominator are EQUAL quantities expressed in different units Example: 1 in. = 2. 54 cm Factors: 1 in. and 2. 54 cm 1 in.

How many minutes are in 2. 5 hours? Conversion factor 2. 5 hr x 1 cancel 60 min 1 hr = 150 min By using dimensional analysis / factor-label method, the UNITS ensure that you have the conversion right side up, and the UNITS are calculated as well as the numbers!

Conversion Factors Write conversion factors that relate each of the following pairs of units: 1000 1 L 1. Liters and m. L = m. L 1000 2. Hours and minutesm. L 1 hr 60 min 3. Meters and kilometers 1000 m 1 km

SI Prefix Conversions 1. Memorize the following chart. (next slide) 2. Find the conversion factor(s). 3. Insert the conversion factor(s) to get to the correct units. 4. When converting to or from a base unit, there will only be one step. To convert to or from any other units, there will be two steps.

SI Prefix Conversions move right move left Prefix teragigamegakilohectodeka. BASE UNIT decicentimillimicronano- Symbol T G M k h da --d c m n Factor 1012 109 106 103 102 101 100 10 -1 10 -2 10 -3 10 -6 10 -9

SI Prefix Conversions a. cm to m b. m to µm c. ns to s d. kg to g 1 m 100 cm 1 m 106 µm 1 s 109 ns 1 kg 1000 g

SI Prefix Conversions 4) 805 Tb = 14 8. 05 x 10 _______ b bytes Terabytes 1012 b 805 Tb 1 1 Tb = 805 x 1012 bytes = 8. 05 x 1014 bytes

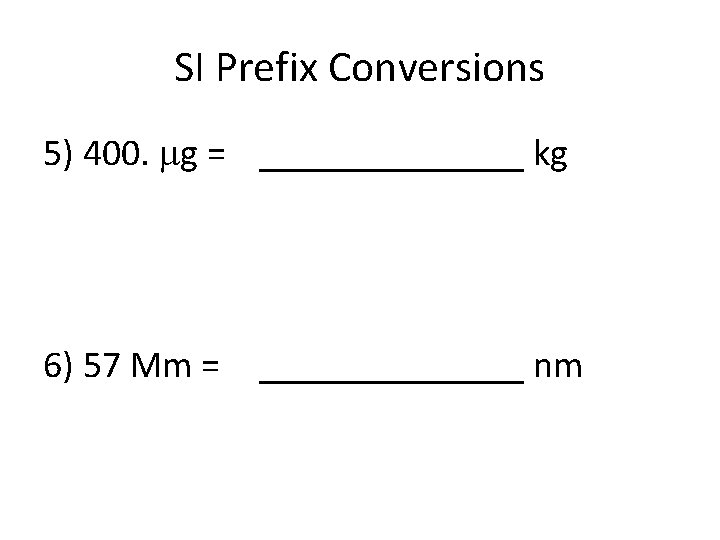
SI Prefix Conversions 5) 400. g = _______ kg 6) 57 Mm = _______ nm

Dimensional Analysis Practice 1. You have $7. 25 in your pocket in quarters. How many quarters do you have?

2. How many seconds are in 1. 4 days? Plan: days hr min seconds

3. How many milliliters are in 1. 00 quart of milk?

4. You have 1. 5 pounds of gold. Find its volume in cm 3 if the density of gold is 19. 3 g/cm 3.

5. Your European hairdresser wants to cut your hair 8. 0 cm shorter. How many inches will he be cutting off?

6. Milton football needs 5. 5 yards for a 1 st down. How many cm is this?

7. A piece of wire is 1. 3 m long. How many 1. 5 cm pieces can be cut from this wire?

8. How many liters of water would fill a container that measures 75. 0 in 3?