Measurement 2 Perimeter l Perimeter The distance around

Measurement 2

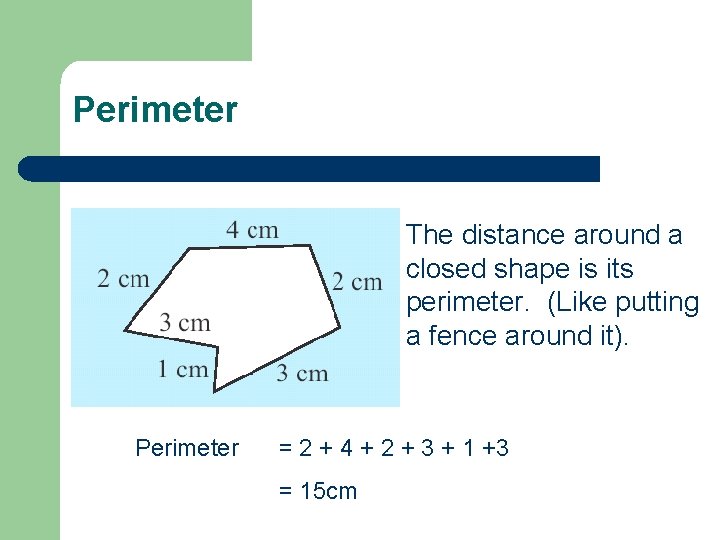
Perimeter l Perimeter The distance around a closed shape is its perimeter. (Like putting a fence around it). = 2 + 4 + 2 + 3 + 1 +3 = 15 cm

Example: Sometimes we have to work out some missing lengths in order to get the perimeter. eg: 13 cm 4 cm 6 cm 9 cm 5 cm 7 cm Perimeter = 13 + 4 + 6 + 5 + 7 + 9 = 44 cm

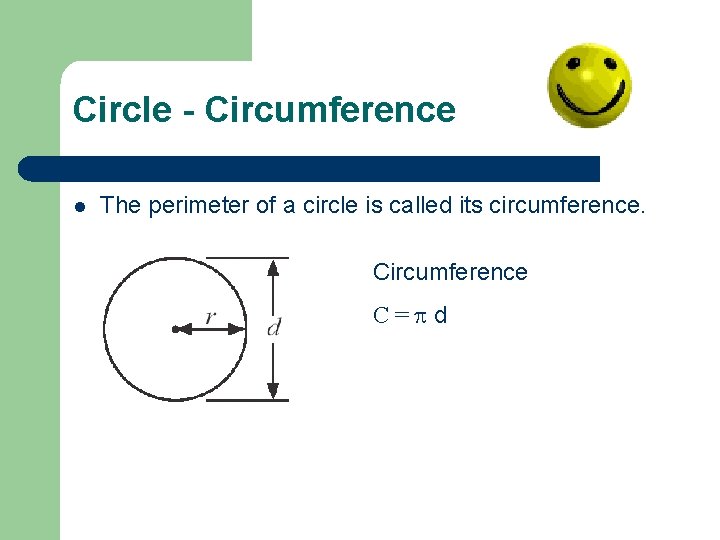
Circle - Circumference l The perimeter of a circle is called its circumference. Circumference C= d

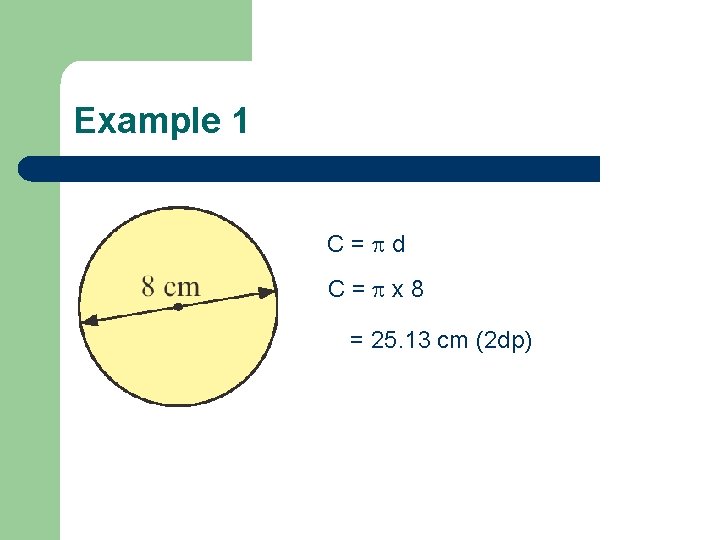
Example 1 C= d C= x 8 = 25. 13 cm (2 dp)

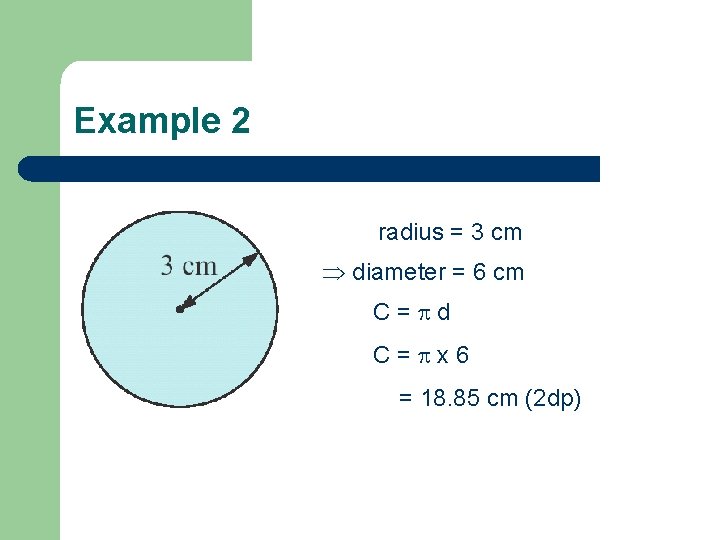
Example 2 radius = 3 cm diameter = 6 cm C= d C= x 6 = 18. 85 cm (2 dp)

Further Examples 3) Perimeter = Half circle circumference + 8 cm = x 8 8 cm 4) 3 cm +8 = 20. 57 cm (2 dp) Perimeter = Quarter circle circumference + 3 cm = 6 x +3+3 = 10. 71 cm (2 dp)

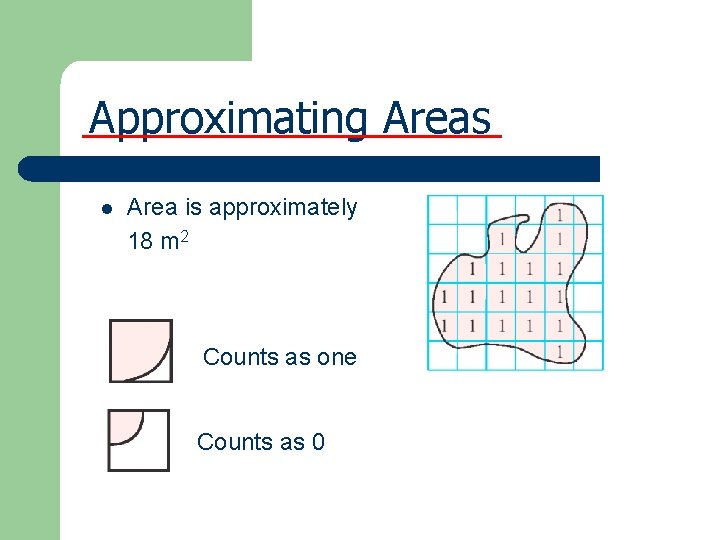
Approximating Areas l Area is approximately 18 m 2 Counts as one Counts as 0

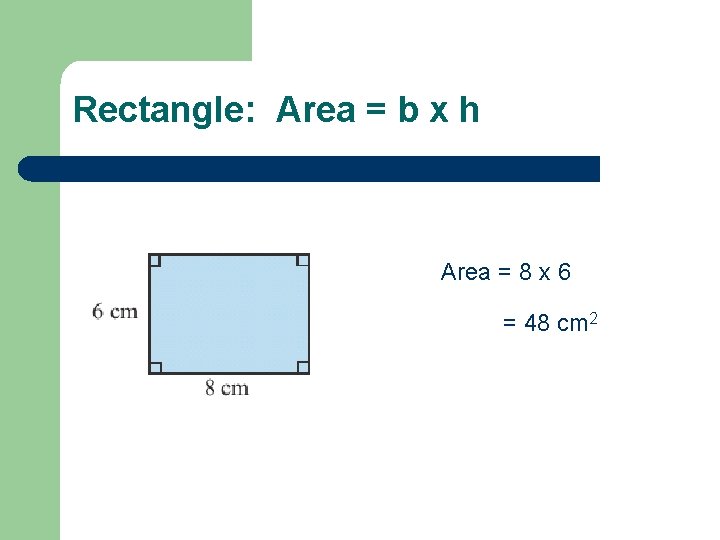
Rectangle: Area = b x h Area = 8 x 6 = 48 cm 2

HECTARE 100 m 1 hectare (1 ha) = 10000 m 2 100 m eg an area of 100 m x 100 m (2 football fields) 1000 m or 1000 m (1 km) x 10 m 10 m or 10000 m x 1 m 1 m or 50 m x 200 m etc 10000 m

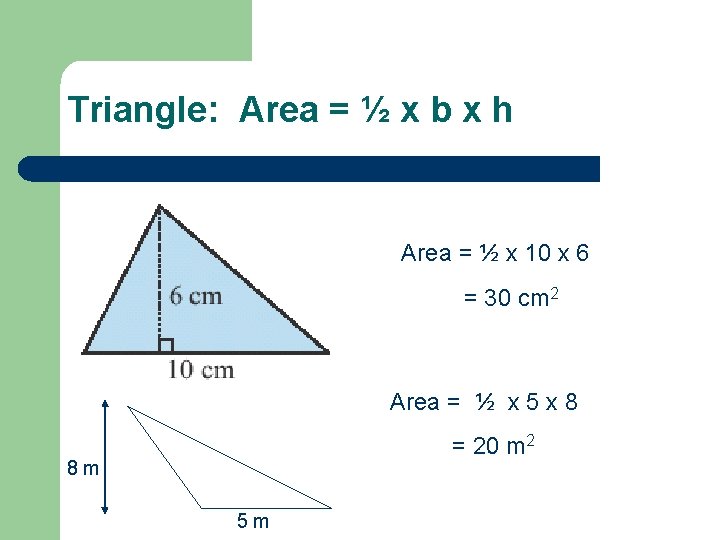
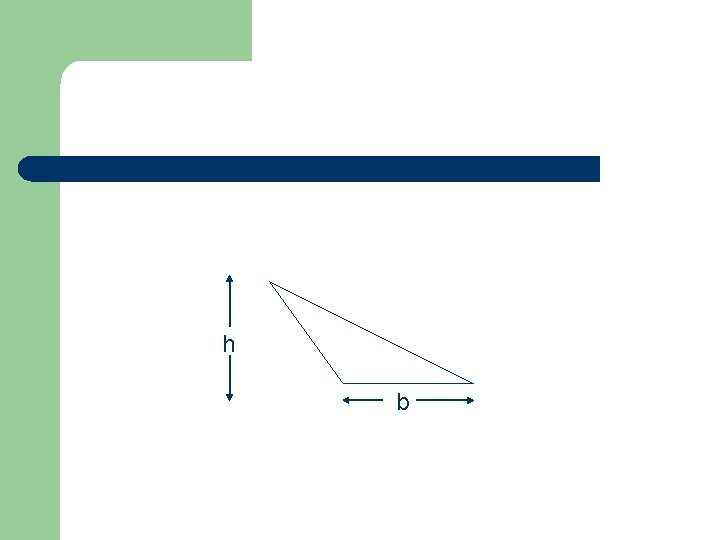
Triangle: Area = ½ x b x h Area = ½ x 10 x 6 = 30 cm 2 Area = ½ x 5 x 8 = 20 m 2 8 m 5 m

h b

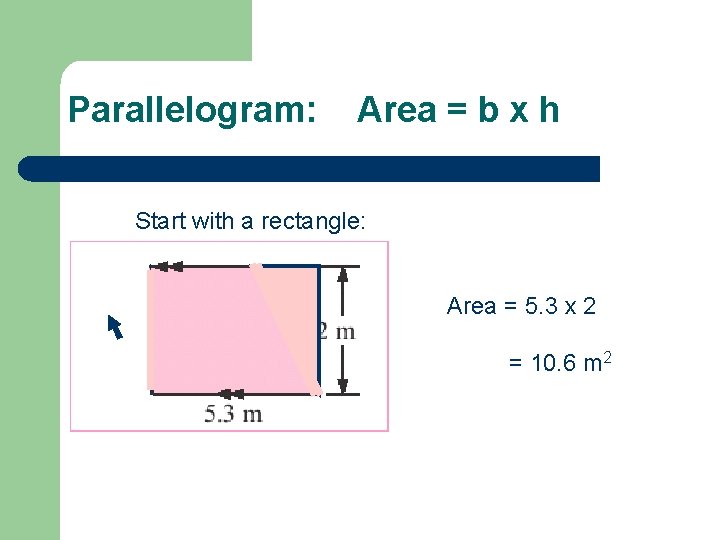
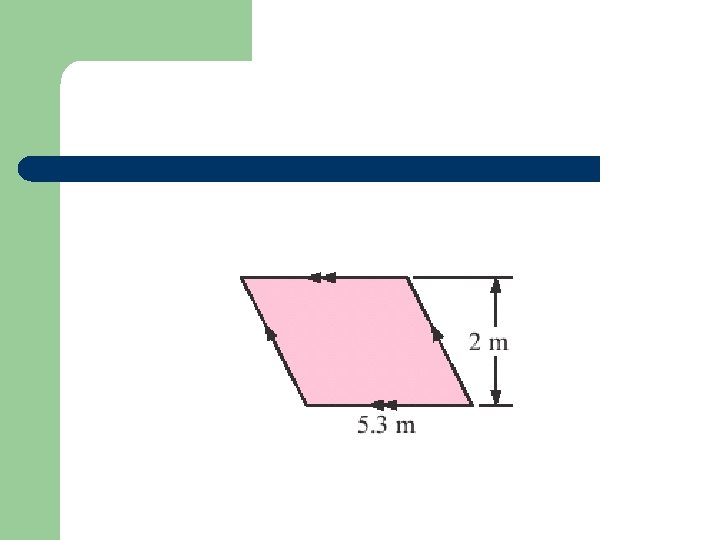
Parallelogram: Area = b x h Start with a rectangle: Area = 5. 3 x 2 = 10. 6 m 2

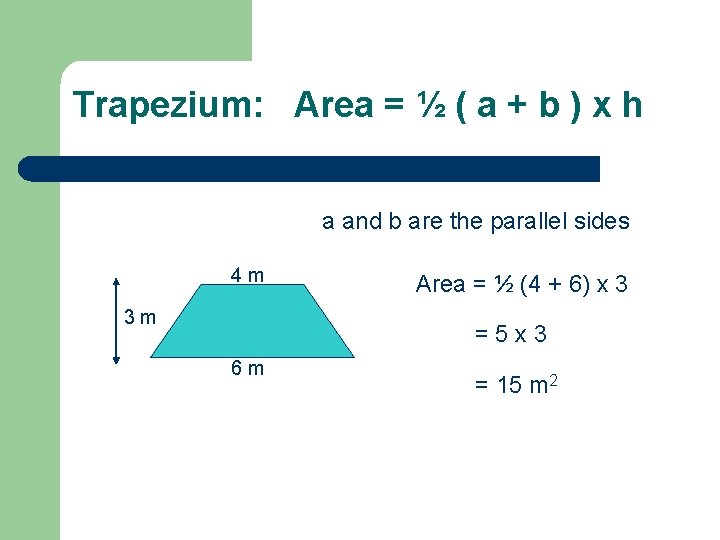
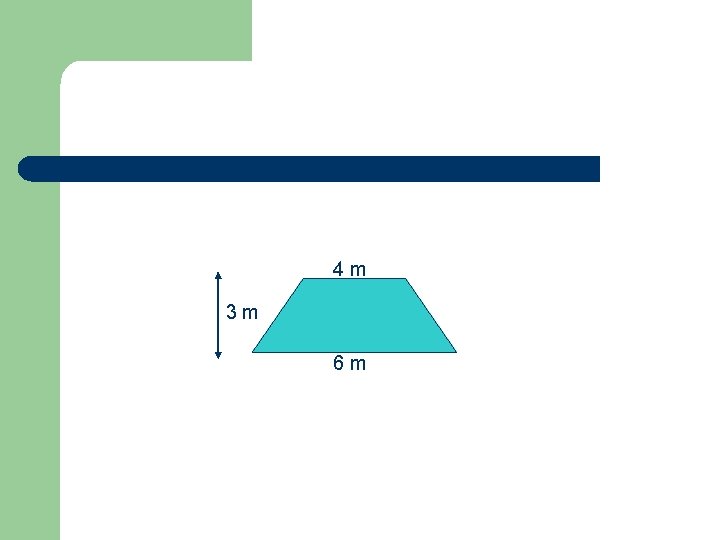
Trapezium: Area = ½ ( a + b ) x h a and b are the parallel sides 4 m 3 m Area = ½ (4 + 6) x 3 =5 x 3 6 m = 15 m 2

4 m 3 m 6 m

actionmath Trapezium example A swimming pool is the shape of a trapezium (on its side) 25 m shallow end 1 m Area = 2 m end deep x 25 = 37. 5 m 2

SONG - Tune of ‘Pop goes the Weasel’ Half the sum of the parallel sides Times the distance between them; That’s the way we calculate The area of a trapezium music

Pop Goes The Weasel SONG - Tune of ‘Pop goes the Weasel’ Half the sum of the parallel sides Times the distance between them; That’s the way we calculate The area of a trapezium

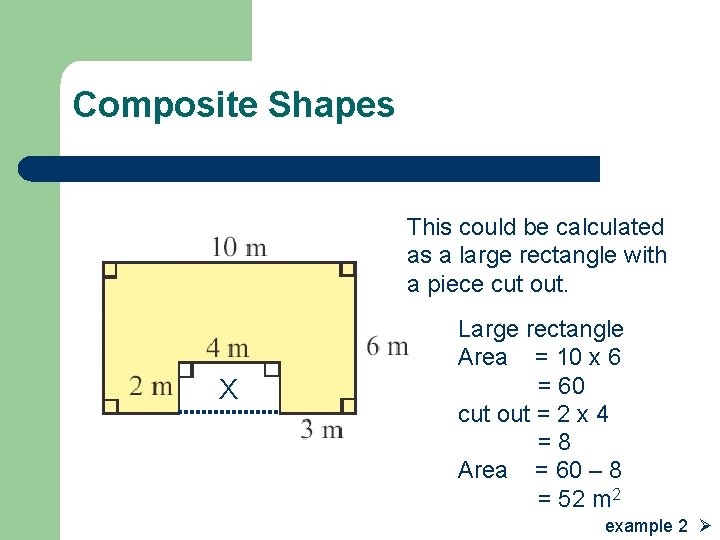
Composite Shapes This could be calculated as a large rectangle with a piece cut out. X Large rectangle Area = 10 x 6 = 60 cut out = 2 x 4 =8 Area = 60 – 8 = 52 m 2 example 2

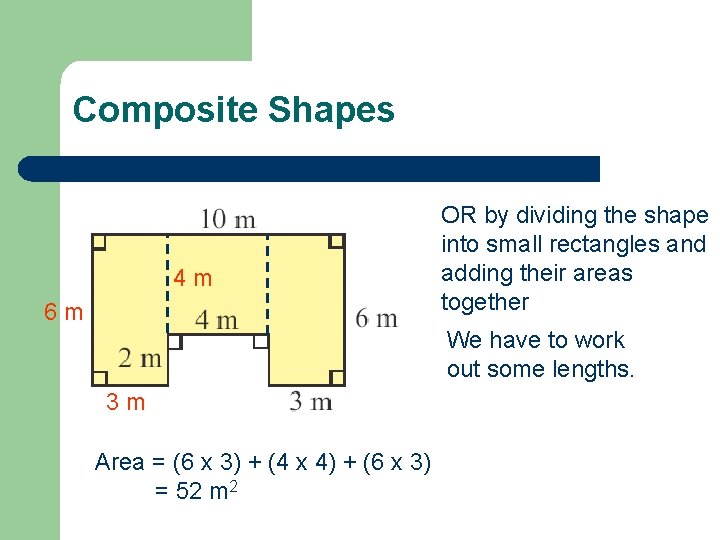
Composite Shapes 4 m 6 m OR by dividing the shape into small rectangles and adding their areas together We have to work out some lengths. 3 m Area = (6 x 3) + (4 x 4) + (6 x 3) = 52 m 2

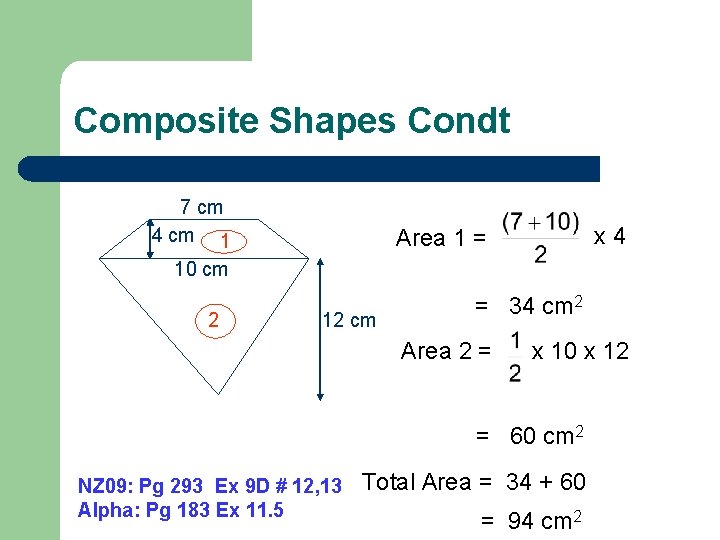
Composite Shapes Condt 7 cm 4 cm 1 x 4 Area 1 = 10 cm 2 12 cm = 34 cm 2 Area 2 = x 10 x 12 = 60 cm 2 NZ 09: Pg 293 Ex 9 D # 12, 13 Alpha: Pg 183 Ex 11. 5 Total Area = 34 + 60 = 94 cm 2

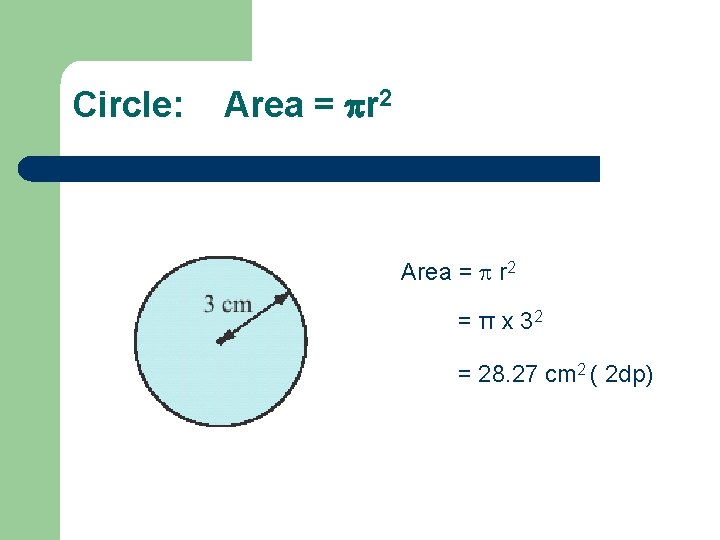
Circle: Area = r 2 Area = r 2 = π x 32 = 28. 27 cm 2 ( 2 dp)

example 2 Area = π r 2 radius = 4 cm (half diameter) Area = x 42 = 50. 27 cm 2 (2 dp)

Further Example 3) Area = circle area x x r 2 8 cm x x 42 = 25. 13 cm 2 (2 dp)

Applications Alpha: Pg 186 Ex 11. 7 Alpha: Pg 195 Ex 12. 3

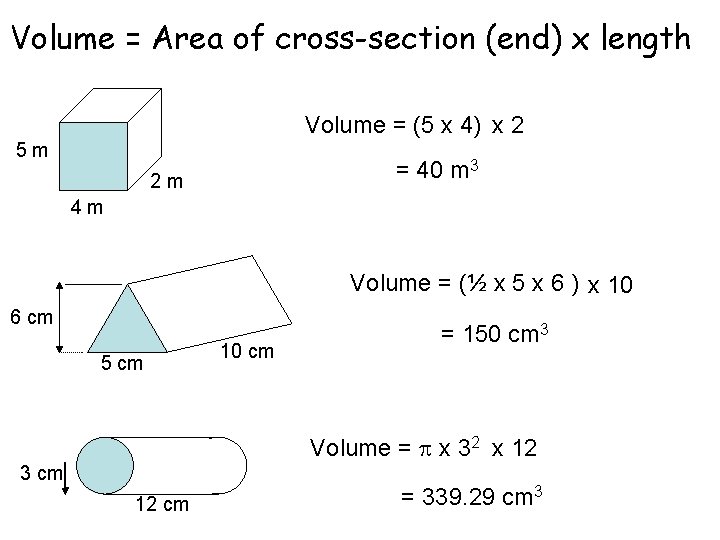
Volume = Area of cross-section (end) x length Volume = (5 x 4) x 2 5 m = 40 m 3 2 m 4 m Volume = (½ x 5 x 6 ) x 10 6 cm 5 cm 10 cm = 150 cm 3 Volume = x 32 x 12 3 cm 12 cm = 339. 29 cm 3

Cubic Capacity l When we talk about volumes of liquids we often use the word capacity, rather than volume. 1000 cc car engine has 1 litre capacity ie 1000 cm 3 holds 1 litre 1000 cm 3 holds 1000 m. L 1 cm 3 holds 1 m. L 1 m 3 holds 1 k. L 1 litre of water weighs 1 kg 1000 m. L of water weighs 1000 g 1 m. L of water weighs 1 g

Surface Area Hey man surface area is easy The surface area of any solid can be found by adding the areas of each of its sides

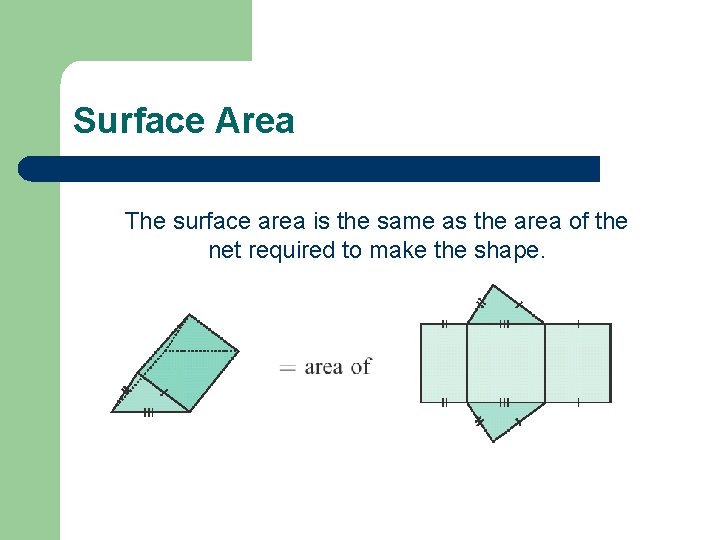
Surface Area The surface area is the same as the area of the net required to make the shape.

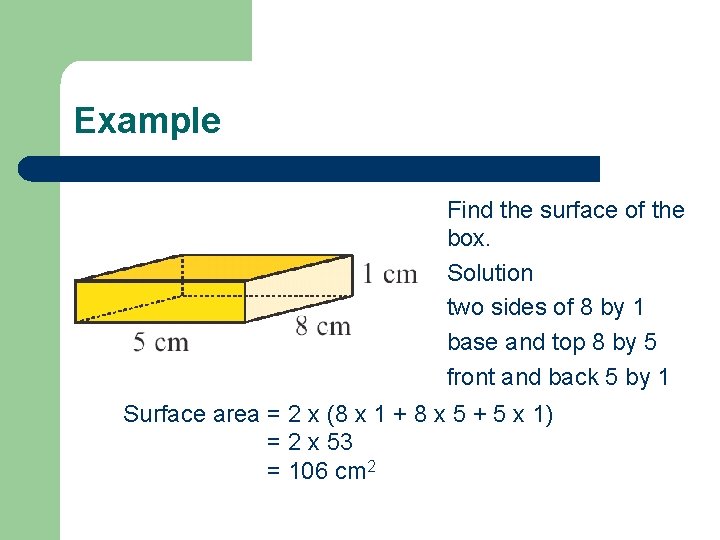
Example Find the surface of the box. Solution two sides of 8 by 1 base and top 8 by 5 front and back 5 by 1 Surface area = 2 x (8 x 1 + 8 x 5 + 5 x 1) = 2 x 53 = 106 cm 2