MEANING OF GRAPHS Position vs Time Graphs Shape

MEANING OF GRAPHS

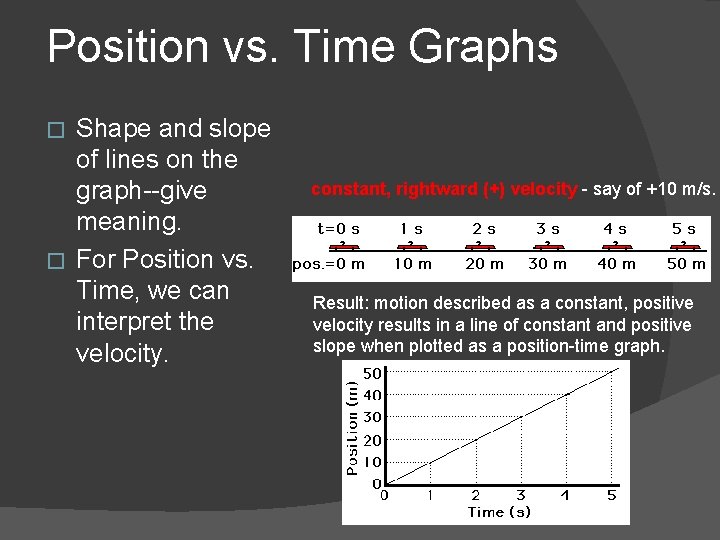
Position vs. Time Graphs Shape and slope of lines on the graph--give meaning. � For Position vs. Time, we can interpret the velocity. � constant, rightward (+) velocity - say of +10 m/s. Result: motion described as a constant, positive velocity results in a line of constant and positive slope when plotted as a position-time graph.

Accelerating Motion rightward (+), changing velocity - that is, a car that is moving rightward but speeding up or accelerating. Result: a motion described as a changing, positive velocity results in a line of changing and positive slope when plotted as a position-time graph. (QUADRATIC)

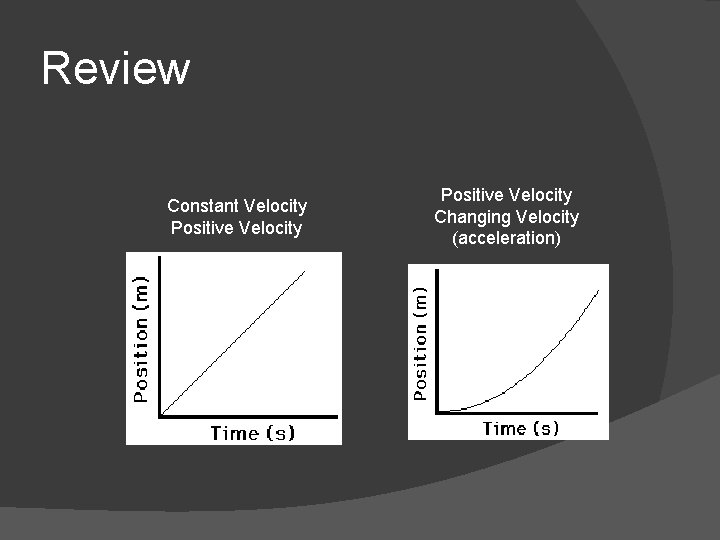
Review Constant Velocity Positive Velocity Changing Velocity (acceleration)

Importance of Slope – P vs. t Remember slope of a line? � Slope reveals info about velocity � “As the slope goes, so goes the velocity” � Constant Velocity=Constant Slope (straight line) � Velocity changes=slope changes (curved line) � Velocity is positive = slope is positive (moving upwards and to the right) � Steeper slope, faster velocity �

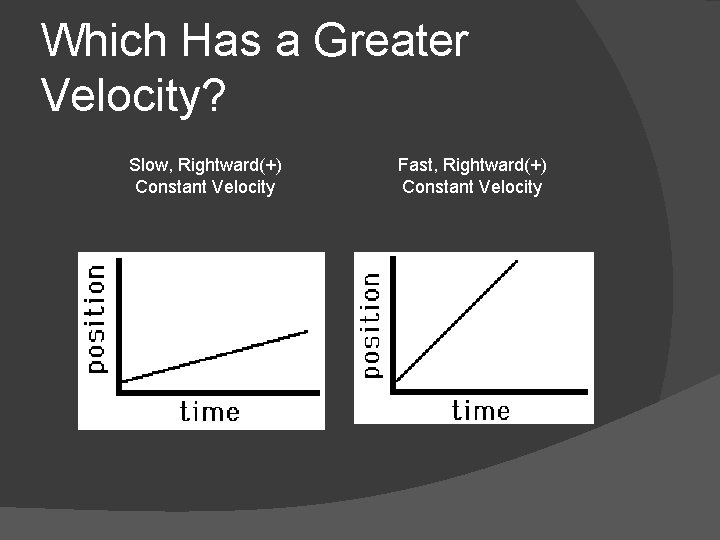
Which Has a Greater Velocity? Slow, Rightward(+) Constant Velocity Fast, Rightward(+) Constant Velocity

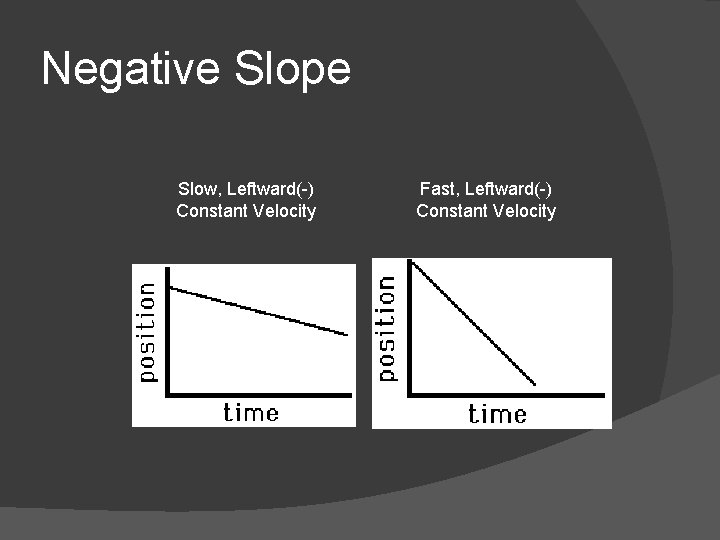
Negative Slope Slow, Leftward(-) Constant Velocity Fast, Leftward(-) Constant Velocity

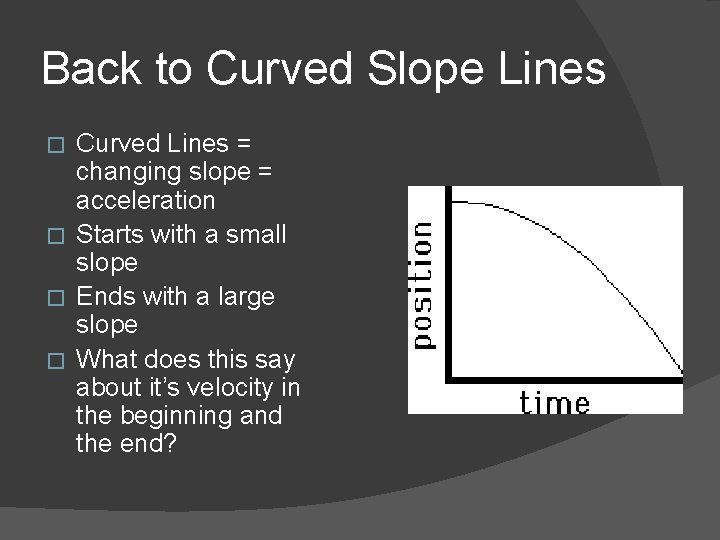
Back to Curved Slope Lines Curved Lines = changing slope = acceleration � Starts with a small slope � Ends with a large slope � What does this say about it’s velocity in the beginning and the end? �

Example: � If Paul walks three meters at 1 m/s, then stops and walks back at 1. 5 m/s, what would the P vs. T graph look like?

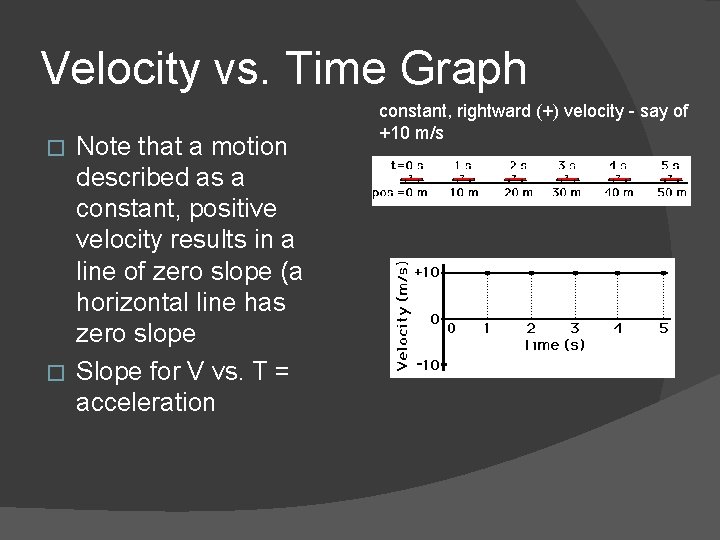
Velocity vs. Time Graph Note that a motion described as a constant, positive velocity results in a line of zero slope (a horizontal line has zero slope � Slope for V vs. T = acceleration � constant, rightward (+) velocity - say of +10 m/s

Accelerated Motion A car that is moving rightward but speeding up or accelerating. � The slope of the line is positive, corresponding to the positive acceleration � rightward (+), changing velocity

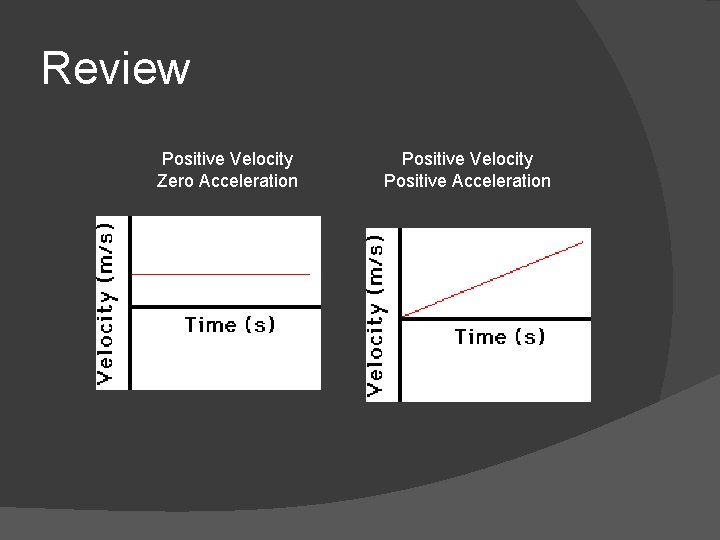
Review Positive Velocity Zero Acceleration Positive Velocity Positive Acceleration

Meaning of Slope V vs. t Slope of a velocity-time graph reveals info about the acceleration. � Acceleration, zero = straight line (zero slope) � Positive acceleration, positive slope (upward line) � Negative acceleration, negative slope (downward sloping line) �

Positive and Negative Positive direction, if it lies above zero. � Negative direction if it lies below zero. � Can be speeding up or slowing down. � If it crosses over zero on x-axis, it changes direction. �

Example � If Paul walks three meters at 1 m/s, then stops and walks back at 1. 5 m/s, what would the V vs. T graph look like?

Speeding up or Slowing down? � � � Speeding up if the magnitude (numerical value) of velocity is getting larger. From 3 m/s to 9 m/s or from -3 m/s to -9 m/s. The number itself is key, not the sign or direction. Speed up: moving away from 0 -velocity line Slowing down: moving towards the 0 -velocity line.