Mean Median and Mode of Ungrouped Data Section







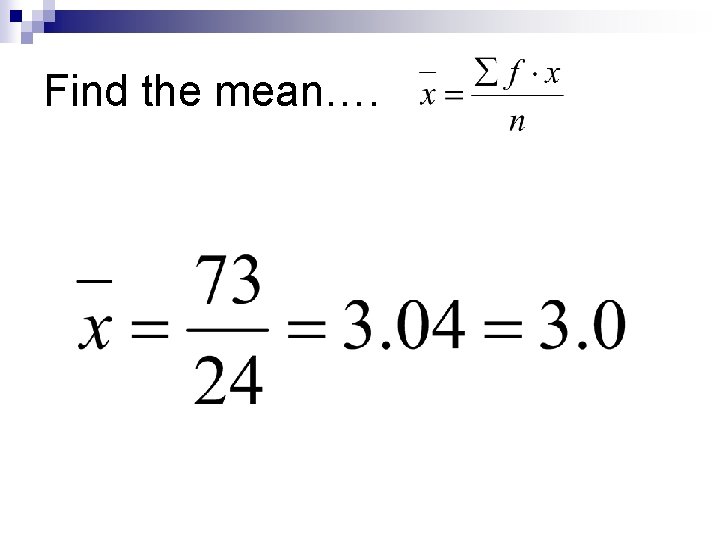




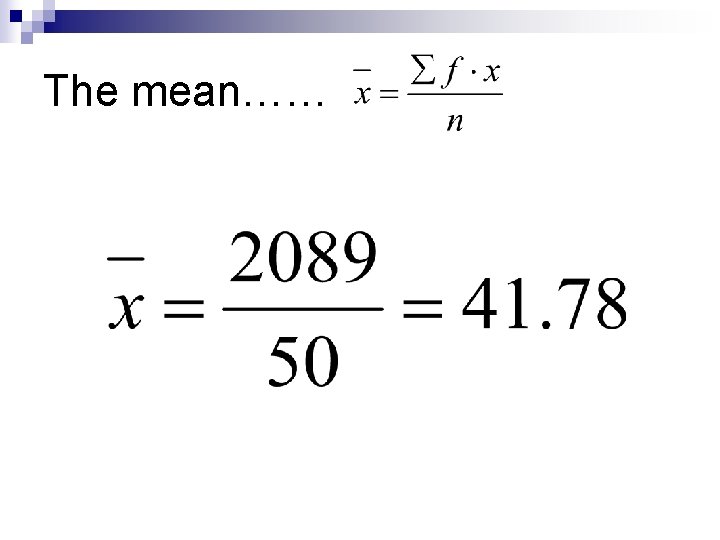










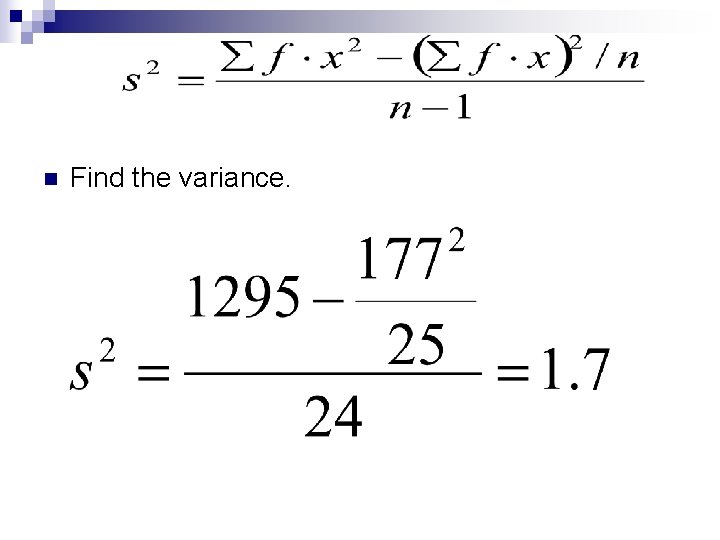






- Slides: 40

Mean, Median, and Mode of Ungrouped Data Section 2. 5

Mean - Ungrouped

Median - Ungrouped n No formula – BUT, we do use a “position locator” formula to show us where to begin to find the median in the cumulative frequency column. (cf) n Position Locator:

Cumulative Frequency - cf n n The cumulative frequency is a column which keeps a running total of the frequencies. Ex: f 10 20 30 40 n =100 cf 10 30 60 100

Mode n Find the number with the greatest frequency (f) and read the “x” value. This is the mode of the set or the value that occurs the most often.

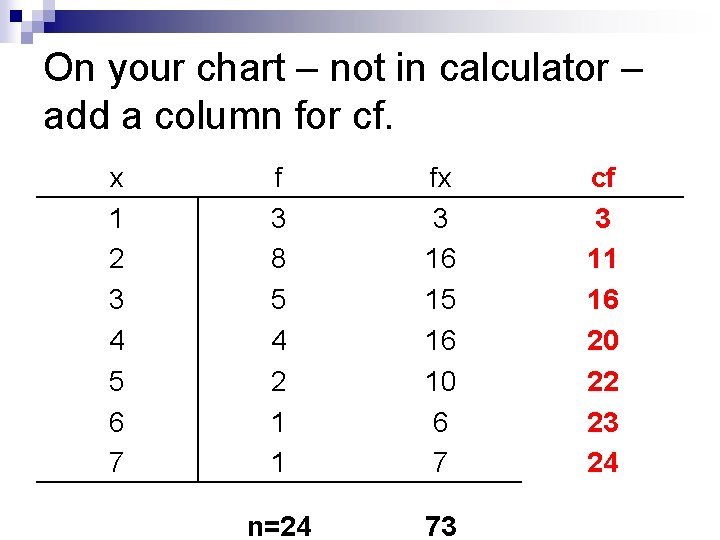
Example n Find the mean, median, and mode of the following data. x 1 2 3 4 5 6 7 f 3 8 5 4 2 1 1 n=24

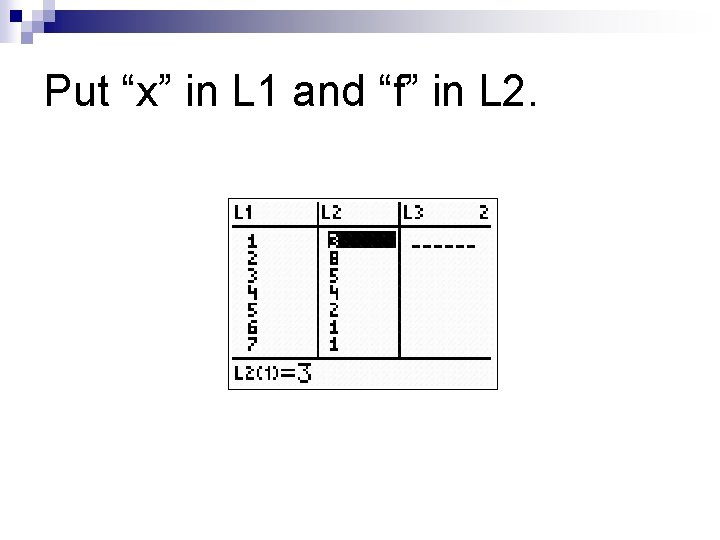
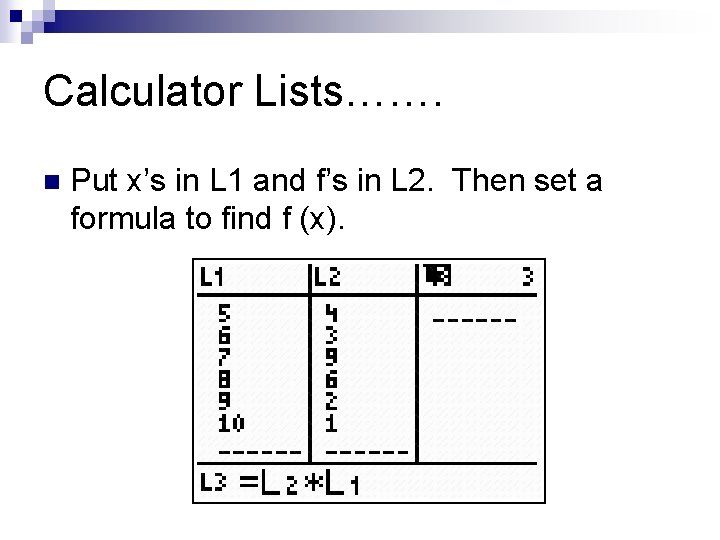
Put “x” in L 1 and “f” in L 2.

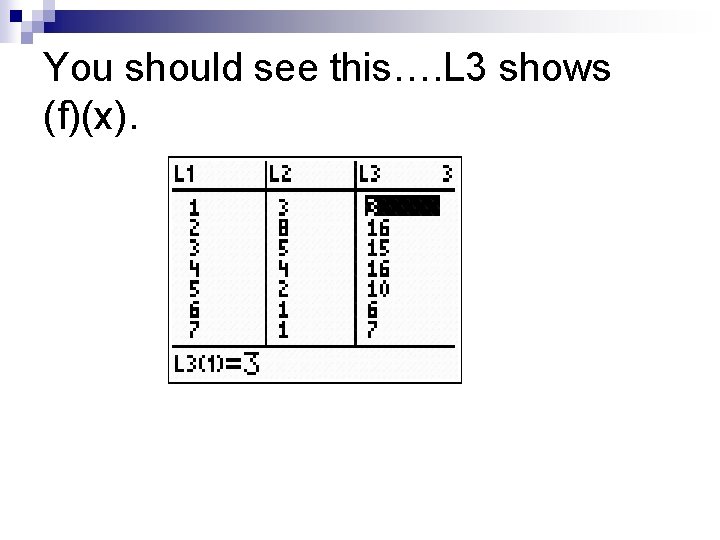
In L 3 set a formula for

You should see this…. L 3 shows (f)(x).

On your chart – not in calculator – add a column for cf. x 1 2 3 4 5 6 7 f 3 8 5 4 2 1 1 fx 3 16 15 16 10 6 7 n=24 73 cf 3 11 16 20 22 23 24
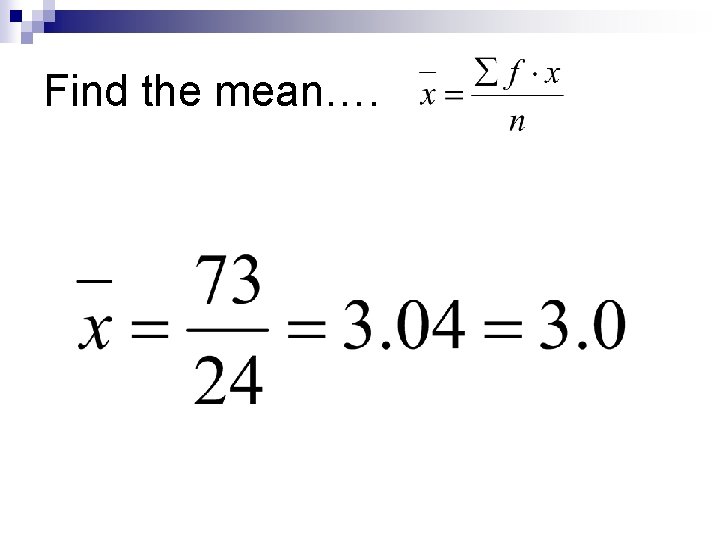
Find the mean….

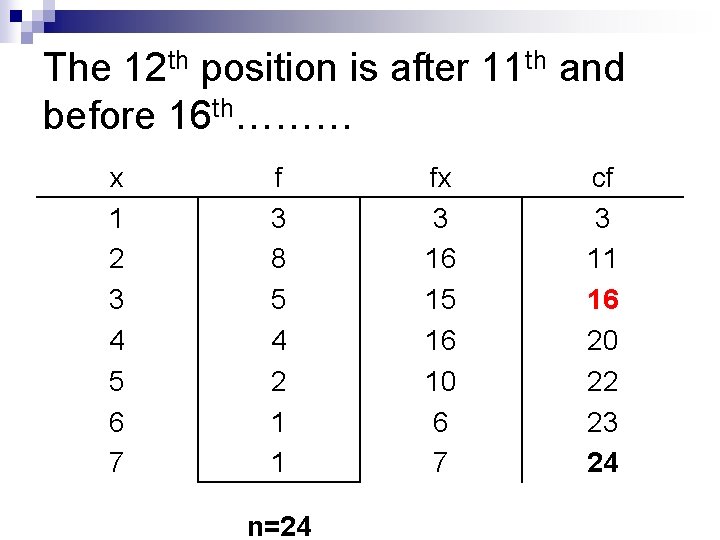
Find the median…… n n/2 = 24/2 = 12 n Locate the class containing the 12 th value in the set in the cumulative frequency column.

The 12 th position is after 11 th and before 16 th……… x 1 2 3 4 5 6 7 f 3 8 5 4 2 1 1 n=24 fx 3 16 15 16 10 6 7 cf 3 11 16 20 22 23 24

Now, read the x value that corresponds to the 12 th position…. n The median is 3. x 1 2 3 4 5 6 7 f 3 8 5 4 2 1 1 n=24 fx 3 16 15 16 10 6 7 cf 3 11 16 20 22 23 24

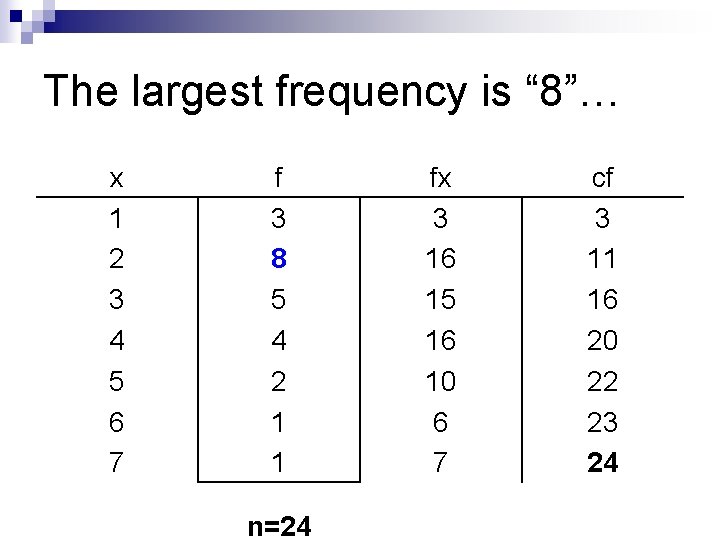
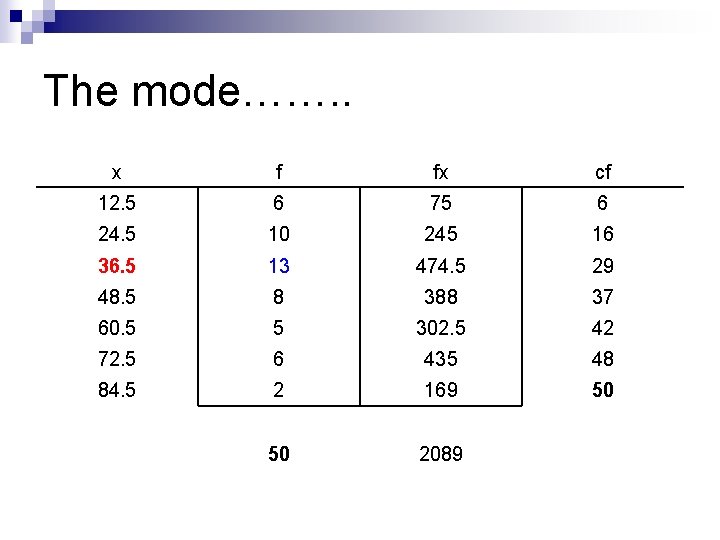
Find the mode……. n Locate the highest frequency and read the x value that corresponds. n NOTE: The mode is not the frequency, it is the x that corresponds to that frequency.

The largest frequency is “ 8”… x 1 2 3 4 5 6 7 f 3 8 5 4 2 1 1 n=24 fx 3 16 15 16 10 6 7 cf 3 11 16 20 22 23 24

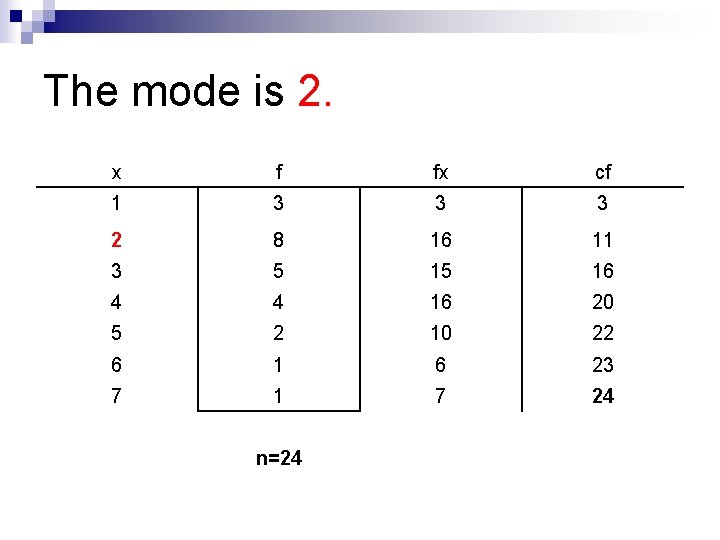
The mode is 2. x f fx cf 1 3 3 3 2 8 16 11 3 5 15 16 4 4 16 20 5 2 10 22 6 1 6 23 7 1 7 24 n=24

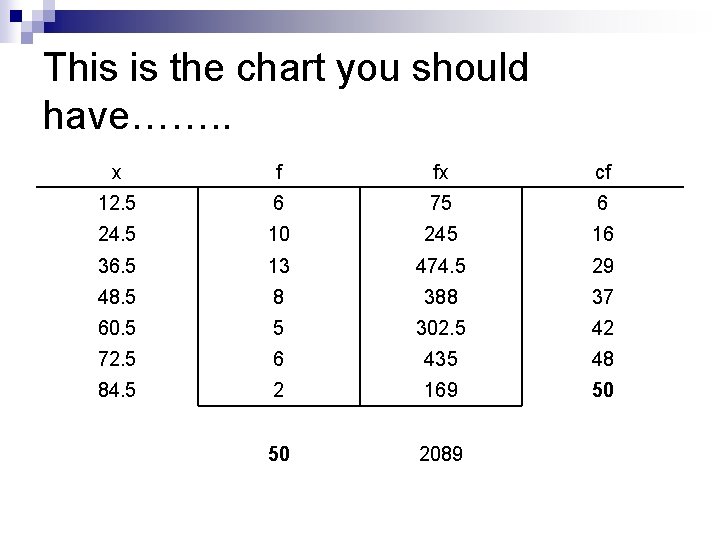
Now, you try……… n Find the mean, median, and mode of the following set of data. x f 12. 5 6 24. 5 10 36. 5 13 48. 5 8 60. 5 5 72. 5 6 84. 5 2 50

This is the chart you should have……. . x f fx cf 12. 5 6 75 6 24. 5 10 245 16 36. 5 13 474. 5 29 48. 5 8 388 37 60. 5 5 302. 5 42 72. 5 6 435 48 84. 5 2 169 50 50 2089
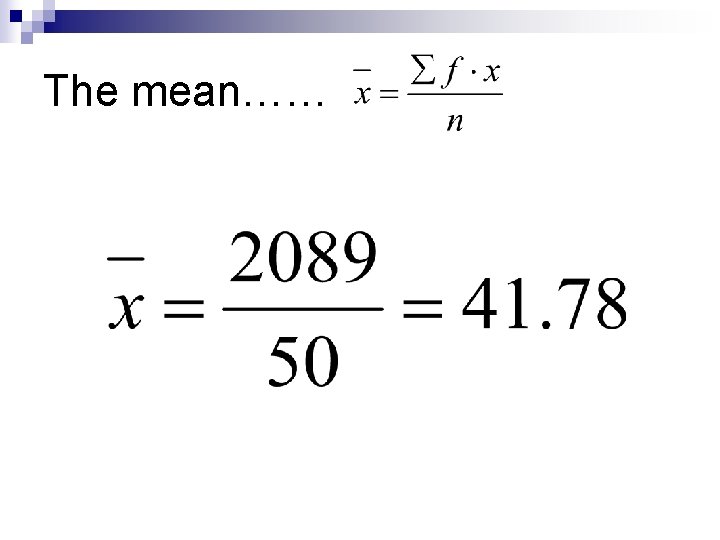
The mean……

The median……. n n/2 = 50/2 = 25 x f fx cf 12. 5 6 75 6 24. 5 10 245 16 36. 5 13 474. 5 29 48. 5 8 388 37 60. 5 5 302. 5 42 72. 5 6 435 48 84. 5 2 169 50 50 2089

The mode……. . x f fx cf 12. 5 6 75 6 24. 5 10 245 16 36. 5 13 474. 5 29 48. 5 8 388 37 60. 5 5 302. 5 42 72. 5 6 435 48 84. 5 2 169 50 50 2089

Now, use the calculator…. . Put “x’s” in L 1 and frequencies in L 2. n Press “Stat”, Calc, One-Var stats, L 1, L 2 and then enter. n n The next slide will show the keystrokes necessary.

Keystrokes….

Screen shows mean. Median can be found as you scroll down…. .

Variance and St. Deviation – Ungrouped Section 2. 5

Variance Formula - Ungrouped

Standard Deviation Formula….

Example - Ungrouped n Find the variance and standard deviation of the set. x 5 6 7 8 9 10 f 4 3 9 6 2 1 n=25

Calculator Lists……. n Put x’s in L 1 and f’s in L 2. Then set a formula to find f (x).

Finding f times x squared…. n Set a formula in L 4

This is what your columns should look like…… x 5 6 7 f 4 3 9 fx 20 18 63 f (x squared) 100 108 441 8 9 10 6 2 1 48 18 10 384 162 100 n=25 177 1295
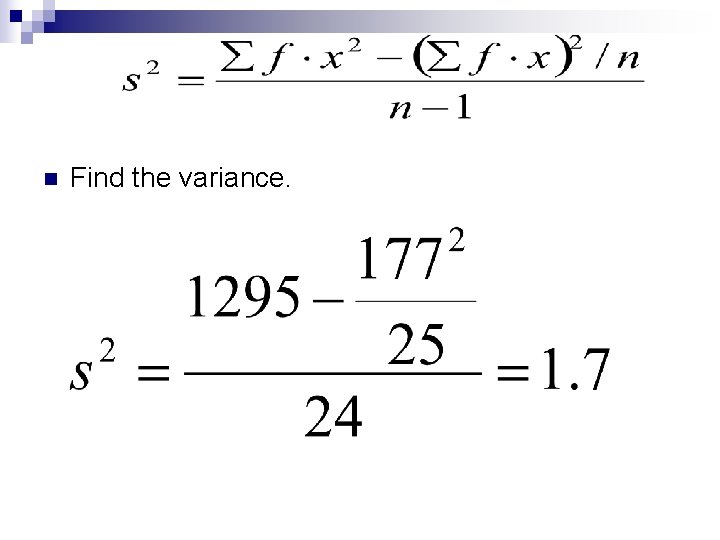
n Find the variance.

n Find the standard deviation.

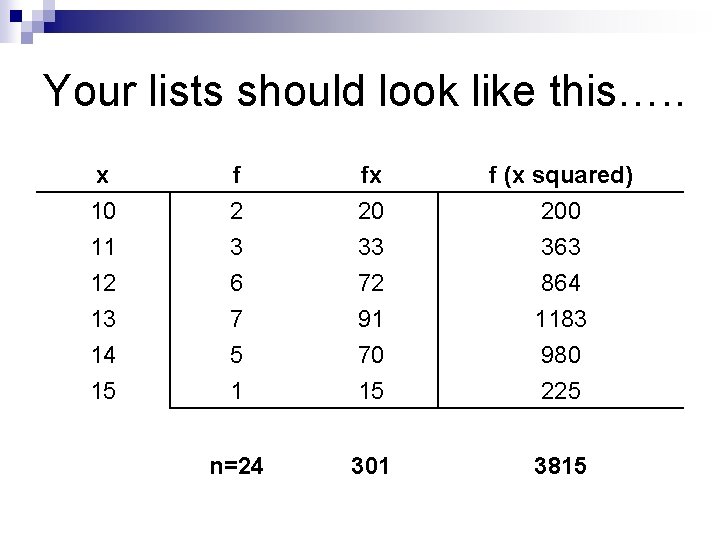
Now you try… n Find the variance and standard deviation of the set. x f 10 2 11 3 12 6 13 7 14 5 15 1 n= 2 4

Your lists should look like this…. . x 10 11 12 f 2 3 6 fx 20 33 72 f (x squared) 200 363 864 13 14 15 7 5 1 91 70 15 1183 980 225 n=24 301 3815

n Find variance.

n Find the standard deviation.

Calculator Only…. . n Put x’s in L 1 and f’s in L 2. Press Stat, Calc, One-var stats, L 1, L 2 enter

Homework n Make sure that you do all the homework BY HAND using the columns. n After you finish, you can check your answers using your calculator.