MEAN ABSOLUTE DEVIATION MAD a measure of data

MEAN ABSOLUTE DEVIATION MAD a measure of data dispersion Tells us how far away the numbers in a data set are from the mean Works well for data that has outliers

MEAN ABSOLUTE DEVIATION

OUTLIER A data point which is far removed in value from the others in the data set It is an unusually large or an unusually small value compared to the others.

OUTLIER EXAMPLE Test scores for 6 students were : 84, 92, 88, 79, 91 and 20. The score of 20 would be an outlier.

MEAN ABSOLUTE DEVIATION 1. Find the mean of the data. 2. Subtract the mean from each value – the result is called the deviation from the mean. 3. Take the absolute value of each deviation from the mean. 4. Find the sum of the absolute values. 5. Divide the total by the number of items.

FIND THE MEAN ABSOLUTE DEVIATION Test scores for 6 students were : 85, 92, 88, 80, 91 and 20. 1. Find the mean: (85+92+88+80+91+20)/6=76 2. Find the deviation from the mean: 85 -76=9 92 -76=16 88 -76=12 80 -76=4 91 -76=15 20 -76=-56

FIND THE MEAN ABSOLUTE DEVIATION Test scores for 6 students were : 85, 92, 88, 80, 91 and 20. 3. Find the absolute value of each deviation from the mean:

FIND THE MEAN ABSOLUTE DEVIATION Test scores for 6 students were : 85, 92, 88, 80, 91 and 20. 4. Find the sum of the absolute values: 9 + 16 + 12 + 4 + 15 + 56 = 112 5. Divide the sum by the number of data items: 112/6 = 18. 7 The mean absolute deviation is 18. 7.

FIND THE MEAN ABSOLUTE DEVIATION Test scores for 6 students were : 85, 92, 88, 80, 91 and 74. 1. Find the mean: (85+92+88+80+91+74)/6=85 2. Find the deviation from the mean: 85 -85=0 92 -85=7 80 -85=-5 91 -85=6 88 -85=3 74 -85=-11

FIND THE MEAN ABSOLUTE DEVIATION Test scores for 6 students were : 85, 92, 88, 80, 91 and 74. 3. Find the absolute value of each deviation from the mean:

FIND THE MEAN ABSOLUTE DEVIATION Test scores for 6 students were : 85, 92, 88, 80, 91 and 74. 4. Find the sum of the absolute values: 0 + 7 + 3 + 5 + 6 + 11 = 32 5. Divide the sum by the number of data items: 32/6 = 5. 3 The mean absolute deviation is 5. 3.

EMMA AND SARA PLAY 5 GAMES ON A HANDHELD VIDEO GAME AND RECORD THEIR SCORES IN THIS TABLE. Game 1 2 3 4 5 Emma 30 20 10 20 20 Sara 15 25 20 25 15 Which girl had the greater mean deviation for her scores?

FIRST, LET’S LOOK AT EMMA’S SCORES Game 1 2 3 4 5 Emma 30 20 10 20 20 1. Find the mean 2. Find the deviation form the mean 3. Take the absolute value of each deviation 4. Find the sum of the absolute values 5. Divide the sum but the number or items

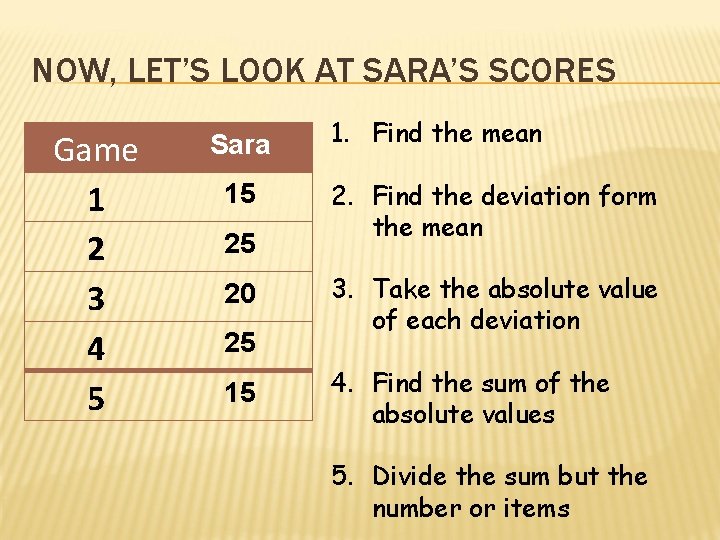
NOW, LET’S LOOK AT SARA’S SCORES Game 1 2 3 4 5 Sara 15 25 20 25 15 1. Find the mean 2. Find the deviation form the mean 3. Take the absolute value of each deviation 4. Find the sum of the absolute values 5. Divide the sum but the number or items

NOW LET’S COMPARE THE DEVIATIONS What was the MAD of Emma’s scores?

HOURLY TIPS Greg $15 $24 $26 $18 $17 Trent $20 $22 $18 $17 • What is Greg’s mean tip money? • What is Trent’s mean tip money? • What is the mean of the combined tip money?

HOURLY TIPS Greg $15 $24 $26 $18 $17 Trent $20 $22 $18 $17 • What is MAD of the combined tip money? • What is Trent’s MAD? • What is Greg’s MAD?

HOURLY TIPS Greg $15 $24 $26 $18 $17 Trent $20 $22 $18 $17 • Whose MAD is closer to the MAD of the combined tip money?