ME 7980 Cardiovascular Biofluid Mechanics 4 Mathematical modeling

ME 7980 Cardiovascular Biofluid Mechanics 4. Mathematical modeling

Objectives • Applications of hydrostatics and steady flow models to describe blood flow in arteries • Unsteady effects: – pressure pulse propagation through arterial wall – Effects of inertial forces due to blood acceleration/deceleration – Effects of artery distensibility on blood flow

Outline • Steady flow considerations and models: – Hydrostatics in circulation – Rigid tube flow model – Application of Bernoulli equation • Unsteady flow models: – Windkessel model for human circulation – Moens-Korteweg relationship (wave propagation, no viscous effects) – Womersley model for blood flow (wave propagation, viscous effects) – Wave propagation in elastic tube with viscous flow (wave propagation, viscous effects)

1. Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hydrostatics in the Circulation • Blood pressure in the “lying down” position – Arterial: 100 mm. Hg – Venous: 2 mm. Hg • Distal pressure is lower Hydrostatic pressure differences in the circulation “lying down” position Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hydrostatics in the Circulation • Blood pressure in the “standing up” position – – Head artery: 50 mm. Hg Leg artery: 180 mm. Hg Head vein: -40 mm. Hg Leg vein: 90 mm. Hg • Pressure differences due to gravitational effects Hydrostatic pressure differences in the circulation “standing up” position Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hydrostatics in the Circulation • Bernoulli equation: • Tube of constant cross section: • Effects of pressure on vessels: – Arteries are stiff: pressure does not affect volume – Veins are distensible: pressure causes expansion Hydrostatic pressure differences in the circulation “standing up” position Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

2. Rigid Tube Flow Model Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hagen Poiseuille Model • Assumptions: – incompressible – steady – laminar – circular cross section • From exact analysis: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hagen Poiseuille Model • Assumptions: Control volume – incompressible – steady – laminar – circular cross section • From control volume analysis: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hagen Poiseuille Model • Validity considerations – Newtonian fluid: reasonable • Casson model: linear at large shear rate – Laminar flow: reasonable • Average flow: Re=1500 (< Recr=2100) • Peak systole: Re = 5100 – Blood vessel : compliance – Flow measurements: no evidence of sustained turbulence – No slip at vascular wall: reasonable • Endothelial cell lining Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Hagen Poiseuille Model • Validity considerations – Steady flow: not valid for most of circulatory system • Pulsatile in arteries – Cylindrical shape: not valid • Elliptical shape (veins, pulmonary arteries) • Taper (most arteries) – Rigid wall: not valid • Arterial wall distends with pulse pressure – Fully developed flow: not valid • Finite length needed to attain fully developed flow • Branching, curved walls Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Blood Vessel Resistance • On time-average basis: – p: time-averaged pressure drop (mm. Hg) – Q: time-averaged flow rate (cm 3/s) – R: resistance to blood flow in segment (PRU, peripheral resistance unit) Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

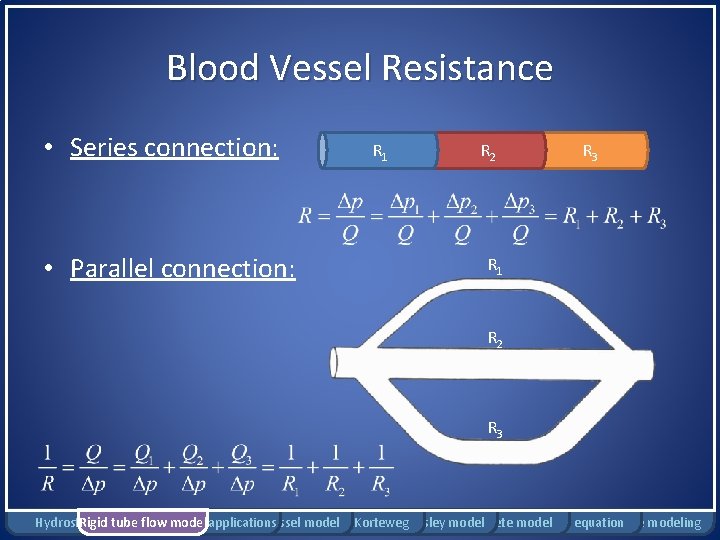
Blood Vessel Resistance • Series connection: • Parallel connection: R 1 R 2 R 3 Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

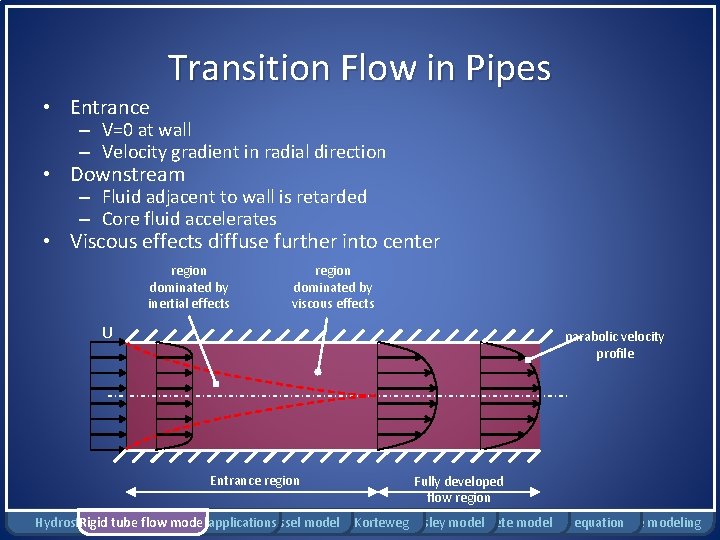
Transition Flow in Pipes • Entrance – V=0 at wall – Velocity gradient in radial direction • Downstream – Fluid adjacent to wall is retarded – Core fluid accelerates • Viscous effects diffuse further into center region dominated by inertial effects region dominated by viscous effects U parabolic velocity profile Entrance region Fully developed flow region Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

BL Thickness and Entrance Length • Balance inertial force and viscous force: • Entrance length definition: – Re > 50: k = 0. 06 – Re 0: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

3. Application of Bernoulli Equation Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Bernoulli Equation • Assumptions: – Steady – Inviscid – Incompressible – Along a streamline Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Stenosis • Narrowing of artery due to: – Fatty deposits – Atherosclerosis p 1, V 1 δ a 1 a 2 p 2, V 2 • Effects of narrowing: – p 1, V 2: known Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Stenosis δ • Arterial flutter – Low pressure at contraction p 1, V 1 – Complete obstruction of vessel under external pressure – Decrease in flow velocity – Increase in pressure – Vessel reopening (cycle) a 1 a 2 p 2, V 2 Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Aneurysm • Definition: Arterial wall bulge at weakening site, resulting in considerable increase in lumen crosssection • Characteristics: – Elastase excess in blood – Decrease in flow velocity – Limited increase in pressure (<5 mm. Hg) – Significant increase in pressure under exercise – Increase in wall shear stress – Bursting of vessel Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

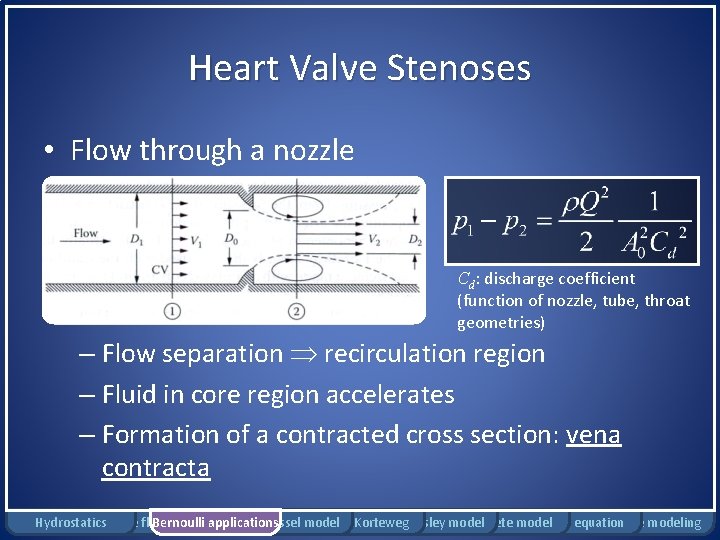
Heart Valve Stenoses • Flow through a nozzle Cd: discharge coefficient (function of nozzle, tube, throat geometries) – Flow separation recirculation region – Fluid in core region accelerates – Formation of a contracted cross section: vena contracta Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

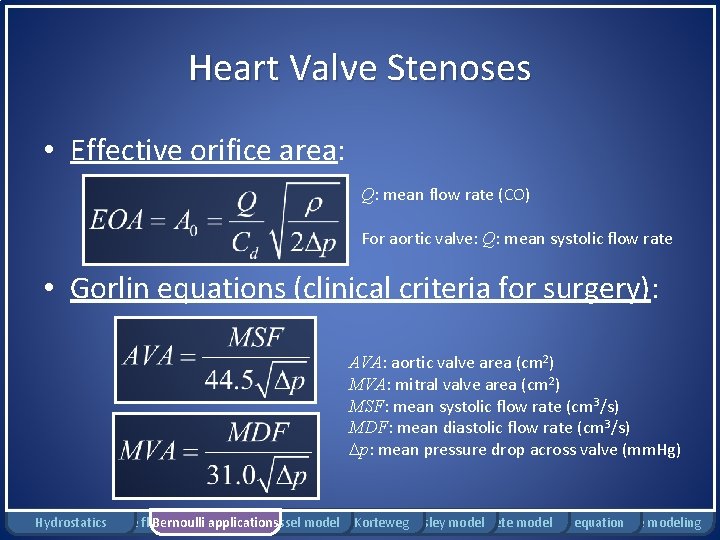
Heart Valve Stenoses • Effective orifice area: Q: mean flow rate (CO) For aortic valve: Q: mean systolic flow rate • Gorlin equations (clinical criteria for surgery): AVA: aortic valve area (cm 2) MVA: mitral valve area (cm 2) MSF: mean systolic flow rate (cm 3/s) MDF: mean diastolic flow rate (cm 3/s) p: mean pressure drop across valve (mm. Hg) Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Heart Valve Stenoses • Effects of flow unsteadiness and viscosity: p = temporal convective viscous + + acceleration dissipation Young, 1979 based on mean values based on peak-systolic values Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

4. Windkessel Models for Human Circulation Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Windkessel Theory • Simplified model • Arterial system modeled as elastic storage vessels Unsteady flow due to pumping of heart Attenuation of unsteady effects due to vessel elasticity Steady flow in peripheral organs • Arteries = interconnected tubes with storage capacity Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

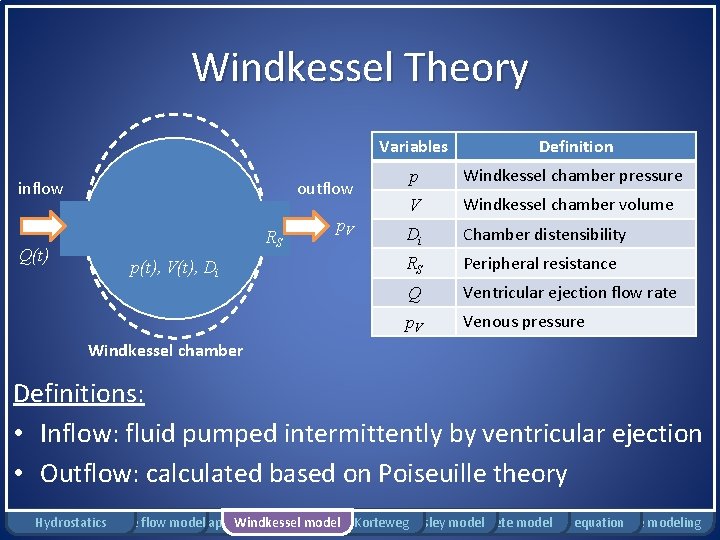
Windkessel Theory inflow Q(t) outflow RS p(t), V(t), Di p. V Variables Definition p Windkessel chamber pressure V Windkessel chamber volume Di Chamber distensibility RS Peripheral resistance Q Ventricular ejection flow rate p. V Venous pressure Windkessel chamber Definitions: • Inflow: fluid pumped intermittently by ventricular ejection • Outflow: calculated based on Poiseuille theory Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Windkessel Solution • Pressure pulse solution – Systole (0 < ts): – Diastole (ts < t < T): p 0: pressure at t=0 p. T: pressure at t=T Windkessel (left) vs. actual (right) pressure pulse • Stroke volume Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Windkessel Theory Summary • Advantages: – Simple model – Prediction of p(t) in arterial system • Limitations: – Model assumes an instantaneous pressure pulse propagation (time for wave transmission is neglected) – Global model does not provide details on structures of flow field Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

5. Moens-Kortweg relationship Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Wave Propagation Characteristics • Speed of transmission depends on wall elastic properties • Pressure pulse: – depends on wall/blood interactions – Changes shape as it travels downstream due to interactions between forward moving wave and waves reflected at discontinuities (branching, curvature sites) Need for model of wave propagation speed Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Moens-Korteweg Relationship • Speed of pressure wave propagation through thin-walled elastic tube containing an incompressible, inviscid fluid • Relationship accounts for: – Fluid motion – Vessel wall motion Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

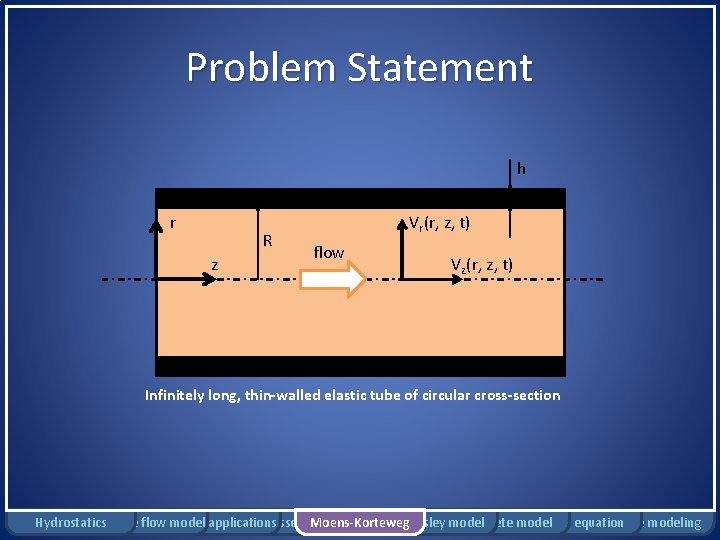
Problem Statement h r R z Vr(r, z, t) flow Vz(r, z, t) Infinitely long, thin-walled elastic tube of circular cross-section Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

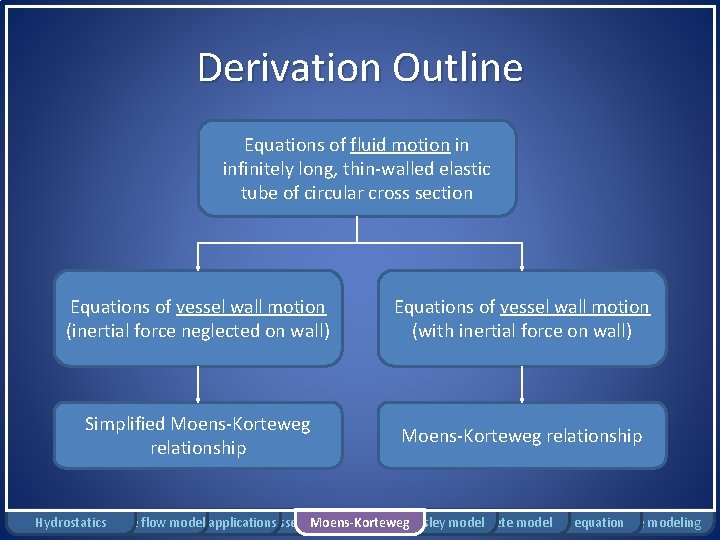
Derivation Outline Equations of fluid motion in infinitely long, thin-walled elastic tube of circular cross section Equations of vessel wall motion (inertial force neglected on wall) Equations of vessel wall motion (with inertial force on wall) Simplified Moens-Korteweg relationship Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Simplified Moens-Korteweg relationship • Reduced Navier-Stokes equations: • Inviscid flow approximation: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

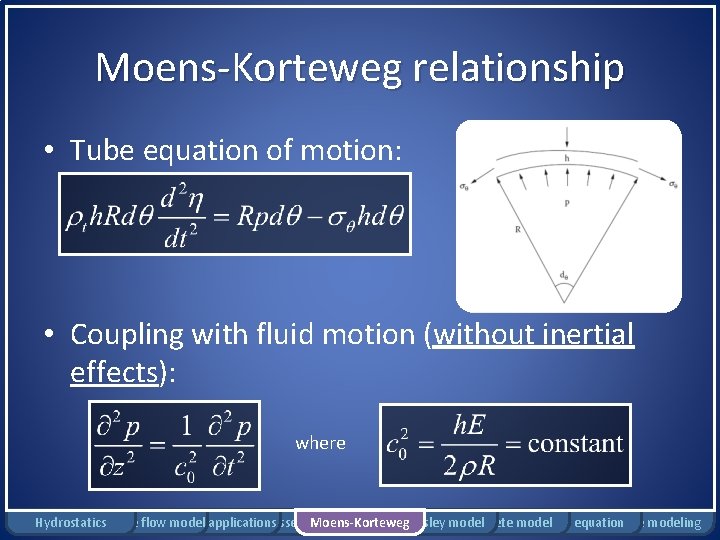
Moens-Korteweg relationship • Tube equation of motion: • Coupling with fluid motion (without inertial effects): where Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

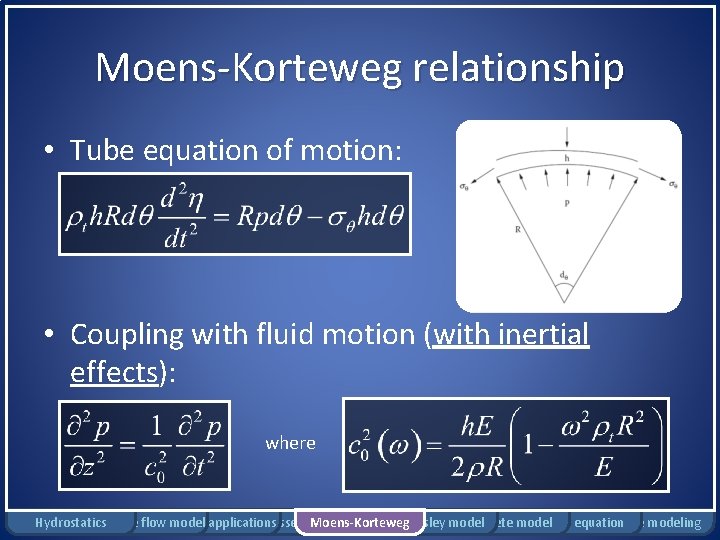
Moens-Korteweg relationship • Tube equation of motion: • Coupling with fluid motion (with inertial effects): where Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

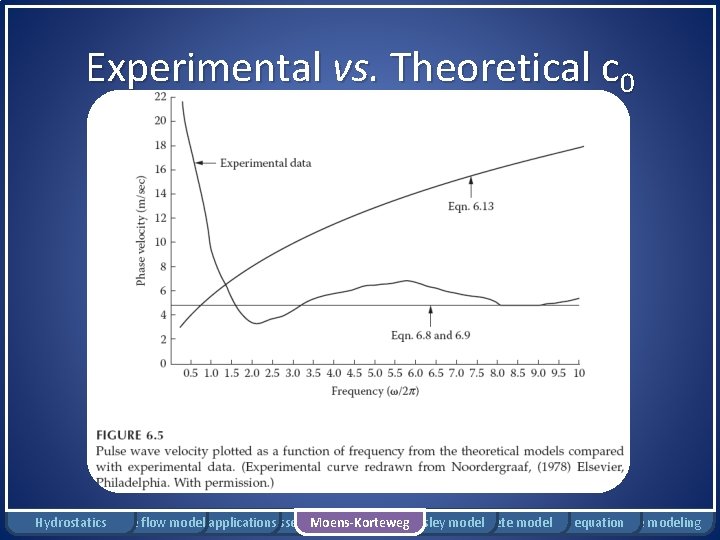
Experimental vs. Theoretical c 0 Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

6. Womersley model for blood flow Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

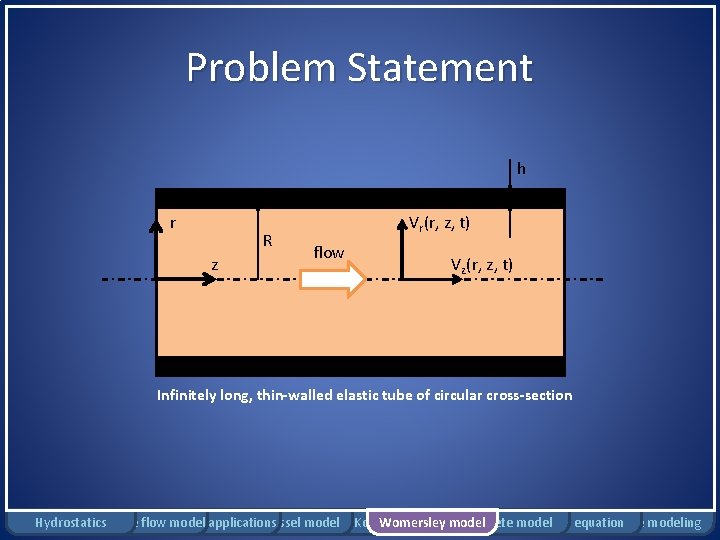
Problem Statement h r R z Vr(r, z, t) flow Vz(r, z, t) Infinitely long, thin-walled elastic tube of circular cross-section Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Problem Assumptions • Flow assumptions: – 2 D – Axisymmetric – No body force – Local acceleration >> convective acceleration • Tube assumptions: – Rigid tube – No radial wall motion ( no radial fluid velocity) Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Equation of Motion • Pressure gradient: • Axial flow velocity magnitude: where: Womersley number Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

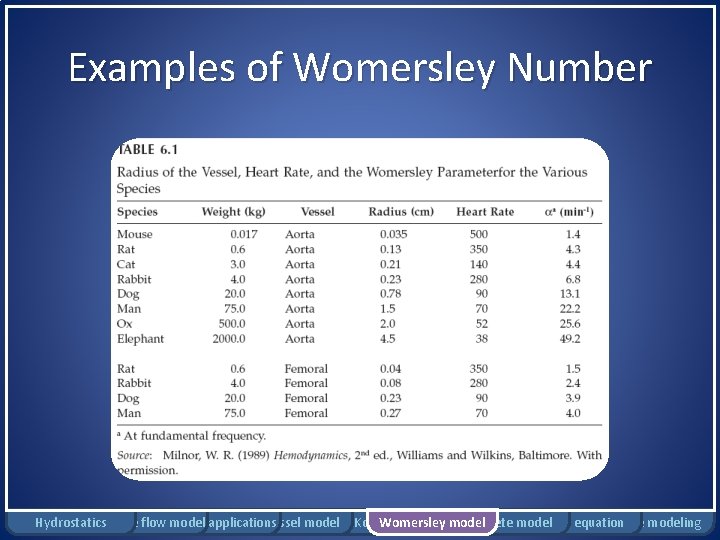
Examples of Womersley Number Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Flow Solution • Flow solution: where: : Bessel function of order k Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

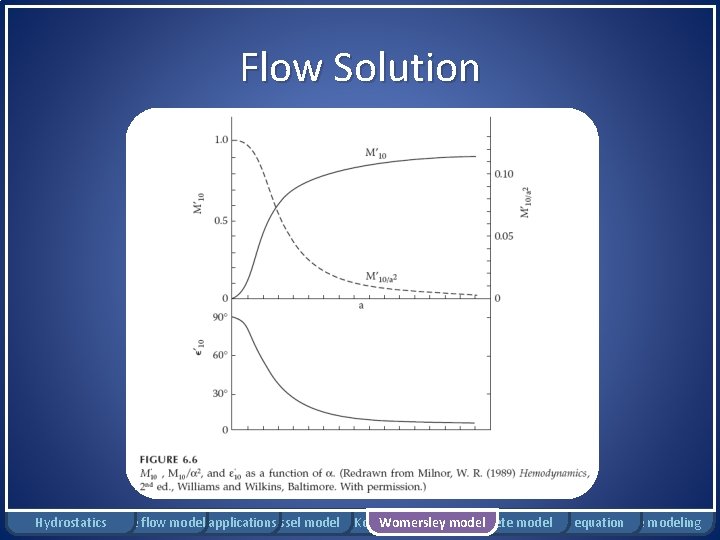
Flow Solution Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

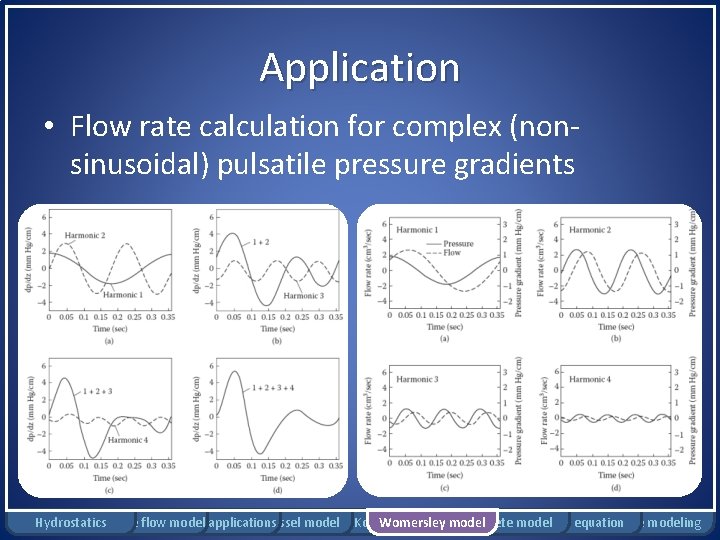
Application • Flow rate calculation for complex (nonsinusoidal) pulsatile pressure gradients Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

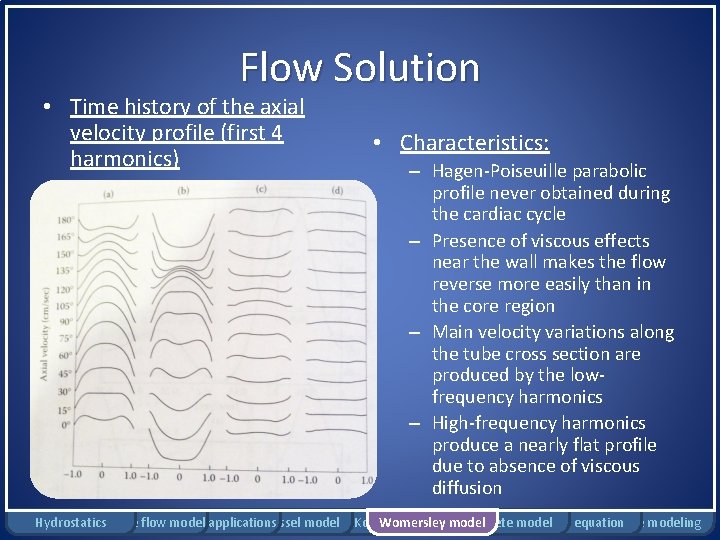
Flow Solution • Time history of the axial velocity profile (first 4 harmonics) • Characteristics: – Hagen-Poiseuille parabolic profile never obtained during the cardiac cycle – Presence of viscous effects near the wall makes the flow reverse more easily than in the core region – Main velocity variations along the tube cross section are produced by the lowfrequency harmonics – High-frequency harmonics produce a nearly flat profile due to absence of viscous diffusion Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

7. Complete model: Wave propagation in elastic tube with viscous flow Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Elastic Tube Equations of Motion Stresses on a tube element Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Elastic Tube and Fluid Stresses • Tube stresses (from Hooke’s law) • Fluid stresses (cylindrical coordinates) Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Elastic Tube Equations of Motion Governing equations of motion for elastic tube • Equations of motion for tube and flow must be solved simultaneously to obtain solutions for: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Flow Equations Governing flow equations • Non-linear inertial terms can be neglected (see order-of-magnitude study performed in Moens-Korteweg derivation) • Along with the 2 tube equations, we obtain a set of 5 equations with 5 unknowns Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Flow Equations Governing flow equations • Boundary conditions at fluid-tube interface: No penetration No slip Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Solutions • All variables are, at least, functions of z and t Seek for solutions that vary as: where: k 1 : wave number (= 1/ ) k 2 : damping constant (decay along z) • Solutions: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Solutions • After performing an order-of-magnitude study, the problem statement reduces to: Equation for 1 NS / z BCs: continuity Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Solutions • By combining the 4 equations and applying the BCs, the problem can be expressed as a system of 2 equations with 2 unknowns: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling

Solutions • Non trivial solutions if and only if determinant of the system = 0 • If (k/ω) = φ is the root of the determinant: Hydrostatics Rigid tube flow Bernoulli model applications Windkessel model Moens-Korteweg Womersley model Complete model Pennes equation Damage modeling