ME 7980 Cardiovascular Biofluid Mechanics 1 Introduction Outline

ME 7980 Cardiovascular Biofluid Mechanics 1. Introduction

Outline 1. 2. 3. Review of mathematics – – Cartesian tensors Green’s and Stoke’s theorems Review of biomechanics – – Principal stresses Equilibrium conditions Deformation analysis and stress-strain relationships Simplifications Review of fluid mechanics – – – Continuum hypothesis Flow field descriptions Conservation laws Stress tensor Equations of motion

1. Review of Mathematics Review of mathematics Review of biomechanics Review of fluid mechanics

Cartesian Tensors • Index notation – Components of are where i = 1, 2, 3 – Unit basis vectors: or • Kronecker delta – Definition: – Property: Review of mathematics If an expression contains ij, one can get rid of ij and set i = j everywhere in the expression Review of biomechanics Review of fluid mechanics

Cartesian Tensors • Summation convention – If a subscript is used twice in a single term, then the sum from 1 to 3 is implied – Example: using index notation: In this expression, the index i is repeated. Therefore, the summation symbol can be dropped. Review of mathematics Review of biomechanics Review of fluid mechanics

Cartesian Tensors • Scalar product Review of mathematics Review of biomechanics Review of fluid mechanics

Cartesian Tensors • Alternating tensor: if is a cyclic permutation of (1, 2, 3) if any two indices are equal If Review of mathematics is not a cyclic permutation of (1, 2, 3) Review of biomechanics Review of fluid mechanics

Cartesian Tensors • Cross product – Definition: – Application to calculation of any cross product: Review of mathematics Review of biomechanics Review of fluid mechanics

Cartesian Tensors • Additional properties and notations: (1) (2) (3) if a is a scalar, then a, i is the gradient of a (4) if ui is a vector, then the divergence of ui is ui, i (5) if is (6) if ui is a vector, then the curl of ui is and are vectors, then the cross product Review of mathematics Review of biomechanics Review of fluid mechanics

Green’s Theorems Volume element: Surface element: Divergence theorem Review of mathematics Review of biomechanics Review of fluid mechanics

Stoke’s Theorem Line element: Review of mathematics Review of biomechanics Review of fluid mechanics

2. Review of Biomechanics Review of mathematics Review of biomechanics Review of fluid mechanics

Continuum Hypothesis • The behavior of a solid/fluid is characterized by considering the average (i. e. , macroscopic) value of the quantity of interest over a small volume containing a large number of molecules • All the solid/fluid characteristics are assumed to vary continuously throughout the solid/fluid • The solid/fluid is treated as a continuum Review of mathematics Review of biomechanics Review of fluid mechanics

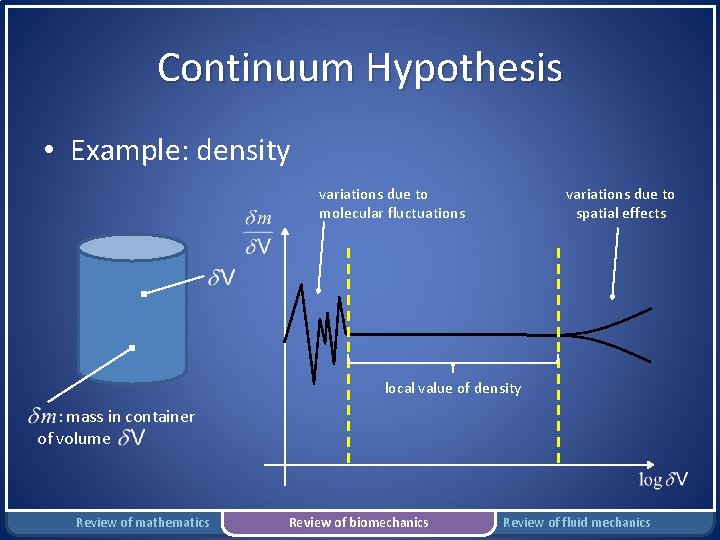
Continuum Hypothesis • Example: density variations due to molecular fluctuations variations due to spatial effects local value of density : mass in container of volume Review of mathematics Review of biomechanics Review of fluid mechanics

Continuum Hypothesis • Conditions for continuum hypothesis: – Smallest volume of interest contains enough molecules to make statistical averages meaningful – Smallest length scale of interest >> mean-free path between molecular collisions Review of mathematics Review of biomechanics Review of fluid mechanics

Cauchy Stress Tensor • Cauchy stress principle: “Upon any imagined closed surface , there exists a distribution of stress vectors whose resultant and moment are equivalent to the actual forces of material continuity exerted by the material outside upon that inside” (Truesdell and Noll, 1965) Review of mathematics Review of biomechanics Review of fluid mechanics

Cauchy Stress Tensor • We assume that only on position surface element Review of mathematics depends at any instant, and orientation of a Review of biomechanics Review of fluid mechanics

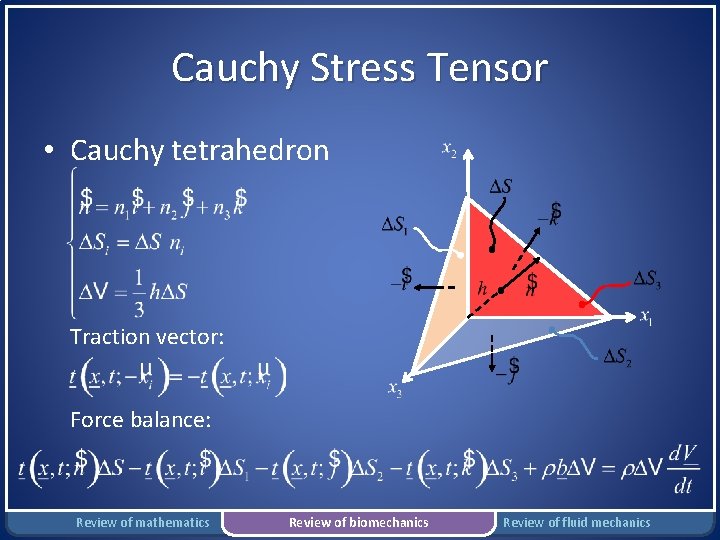
Cauchy Stress Tensor • Cauchy tetrahedron Traction vector: Force balance: Review of mathematics Review of biomechanics Review of fluid mechanics

Cauchy Stress Tensor As h 0: or: where is the stress tensor Notation: is the j th component of the stress exerted on the surface whose unit normal is in the i-direction Review of mathematics Review of biomechanics Review of fluid mechanics

Cauchy Stress Tensor • The stress tensor defines the state of material interaction at any point Ax : normal stress (generated by force Fi on Ai) : shearing stress (generated by force Fj on Ai) Review of mathematics Review of biomechanics Review of fluid mechanics

Principal Stresses • Force and moment balance yield: Cauchy stress tensor is symmetric (6 components) • Reduced form: : principal stresses (act in mutually perpendicular directions, normal to 3 principal planes in which all shearing stresses are zero) Review of mathematics Review of biomechanics Review of fluid mechanics

Principal Stresses • Von Mises stress: (used to determine locations of max stresses (e. g. , aneurysms, stent-grafts) Review of mathematics Review of biomechanics Review of fluid mechanics

Equilibrium Conditions Ax • Differential volume to: exposed – Surfaces forces (internal forces) – Body forces (external forces) : body force per unit mass Conditions of static equilibrium: Review of mathematics Review of biomechanics Review of fluid mechanics

Deformation Analysis A A’ d. S (X +d. X ) i i B (xi) (Xi) initial state ds B’ (xi+dxi) deformed state • Displacement vector: • Change in element length: : Lagrangian Green’s strain tensor Review of mathematics : Eulerian Cauchy’s strain tensor Review of biomechanics Review of fluid mechanics

Deformation Analysis A A’ d. S (X +d. X ) i i B (xi) (Xi) initial state ds B’ (xi+dxi) deformed state • Small displacements: Review of mathematics Review of biomechanics Review of fluid mechanics

Stress-Strain Relationships: Elastic Behavior • Describe material mechanical properties • Generalized Hooke’s law: • Isotropic elastic solid: : Lamé elastic constants : Poisson’s ratio E: Young’s modulus G: shear modulus Review of mathematics Review of biomechanics Review of fluid mechanics

Stress-Strain Relationships: Elastic Behavior • Young’s modulus (elastic modulus): Stress (N/m 2) Linear elastic (Hookean) material E Strain (%) • Poisson’s ratio: y z • Shear modulus: x P Isotropic material Homogeneous, isotropic material Review of mathematics Review of biomechanics Review of fluid mechanics

Stress-Strain Relationships: Viscoelastic Models • Maxwell model k • Voigt model k where: Review of mathematics Review of biomechanics (rate of relaxation) Review of fluid mechanics

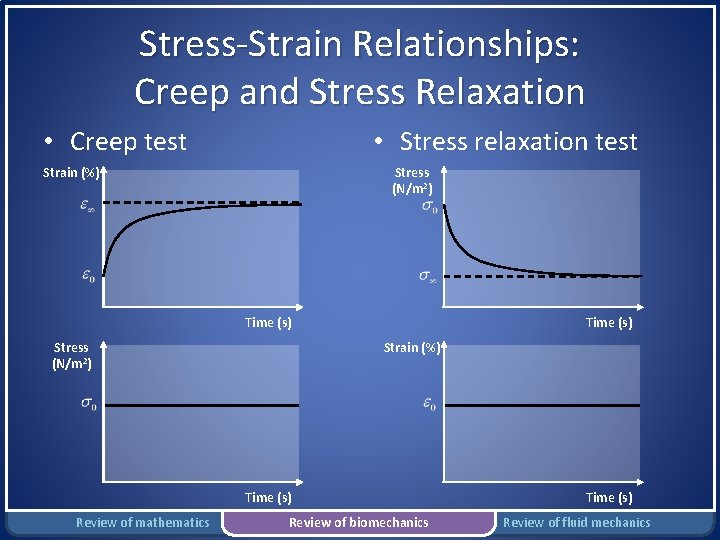
Stress-Strain Relationships: Creep and Stress Relaxation • Creep test • Stress relaxation test Strain (%) Stress (N/m 2) Time (s) Strain (%) Time (s) Review of mathematics Review of biomechanics Time (s) Review of fluid mechanics

Stress-Strain Relationships: Elastic Behavior • Hooke’s law (cylindrical coordinates): Review of mathematics Review of biomechanics Review of fluid mechanics

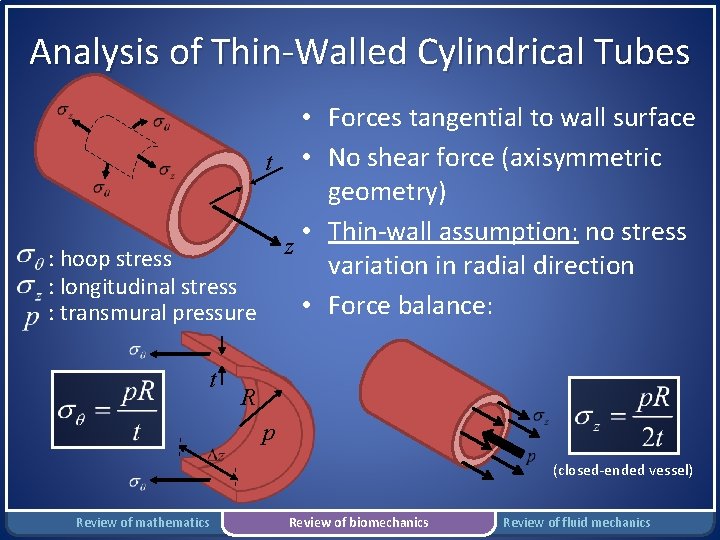
Analysis of Thin-Walled Cylindrical Tubes • Forces tangential to wall surface t • No shear force (axisymmetric geometry) • Thin-wall assumption: no stress z : hoop stress variation in radial direction : longitudinal stress • Force balance: : transmural pressure t R p (closed-ended vessel) Review of mathematics Review of biomechanics Review of fluid mechanics

Analysis of Thin-Walled Cylindrical Tubes : hoop stress : longitudinal stress : transmural pressure • Forces tangential to wall surface t • No shear force (axisymmetric geometry) • Thin-wall assumption: no stress z variation in radial direction Initial circumferential length: Final circumferential length: Review of mathematics Review of biomechanics Review of fluid mechanics

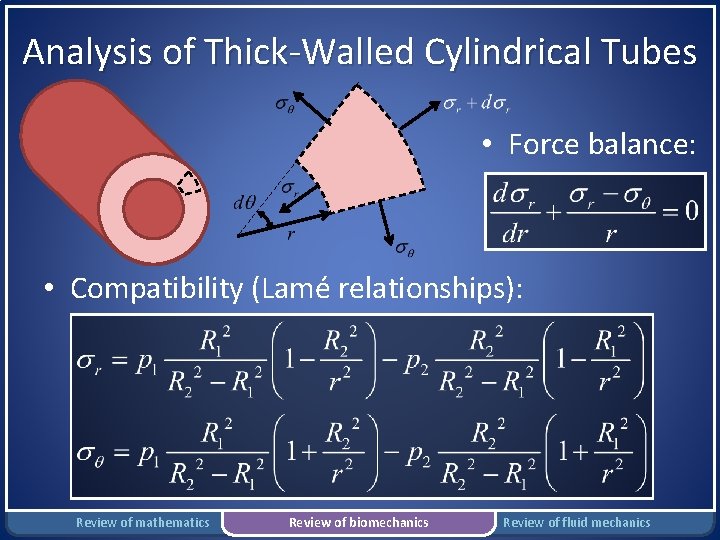
Analysis of Thick-Walled Cylindrical Tubes • Force balance: • Compatibility (Lamé relationships): Review of mathematics Review of biomechanics Review of fluid mechanics

3. Review of Fluid Mechanics Review of mathematics Review of biomechanics Review of fluid mechanics

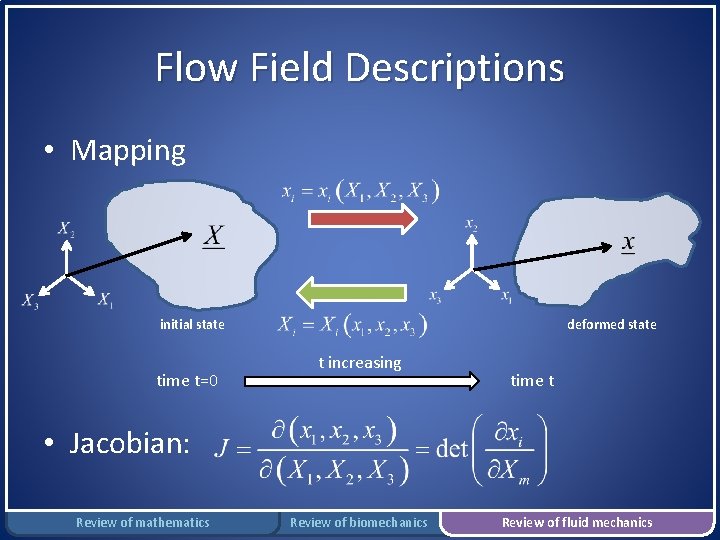
Flow Field Descriptions • Mapping initial state time t=0 deformed state t increasing time t • Jacobian: Review of mathematics Review of biomechanics Review of fluid mechanics

Flow Field Descriptions • Spatial (Eulerian) description: Measurements at specified locations in space (laboratory coordinates) • Material (Lagrangian) description: Follows individual fluid particles Review of mathematics Review of biomechanics Review of fluid mechanics

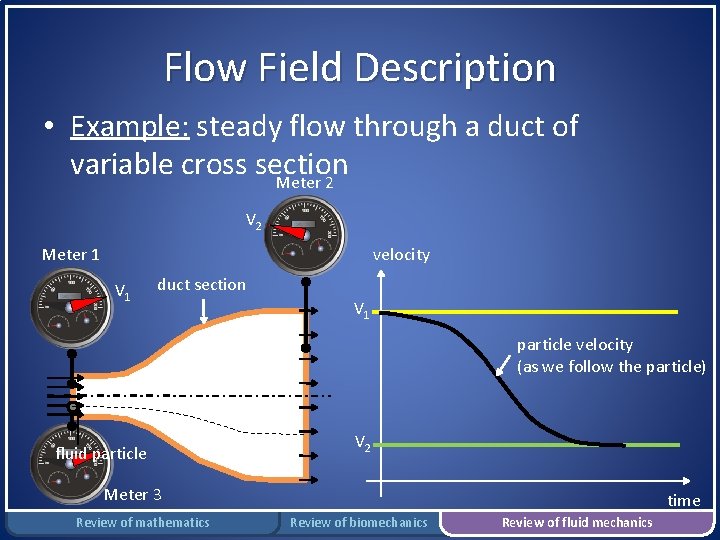
Flow Field Description • Example: steady flow through a duct of variable cross section Meter 2 V 2 Meter 1 velocity V 1 duct section V 1 particle velocity (as we follow the particle) fluid particle V 2 Meter 3 Review of mathematics time Review of biomechanics Review of fluid mechanics

Flow Field Descriptions • If f is some property of the fluid in spatial coordinates (scalar or vector property): material • Likewise, if G is a property in material coordinates: Review of mathematics Review of biomechanics Review of fluid mechanics

Flow Field Descriptions • Spatial vs. material derivatives: Position fixed Particle fixed Review of mathematics Review of biomechanics Review of fluid mechanics

Flow Field Descriptions • Acceleration field: if: then, using the chain rule: Review of mathematics Review of biomechanics Review of fluid mechanics

Conservation Laws • Reynolds Transport Theorem: – – : arbitrary volume moving with the fluid : scalar or vector, function of position Alternate form: Review of mathematics rate of increase of F in V(t) flux of F through S(t) Review of biomechanics Review of fluid mechanics

Conservation Laws • Continuity: – Let be the mass of fluid within – Conservation of mass requires: : density Alternate form: Review of mathematics Review of biomechanics Review of fluid mechanics

Conservation Laws • Linear momentum: – Balance of linear momentum requires: : density : body forces Alternate form: Review of mathematics Review of biomechanics Review of fluid mechanics

Constitutive Equations Perfect fluid behavior Viscous fluid behavior • Only normal stresses • Stoke’s postulate: : rate of deformation tensor • Linear momentum balance: Review of mathematics • Linear momentum balance: Review of biomechanics Review of fluid mechanics

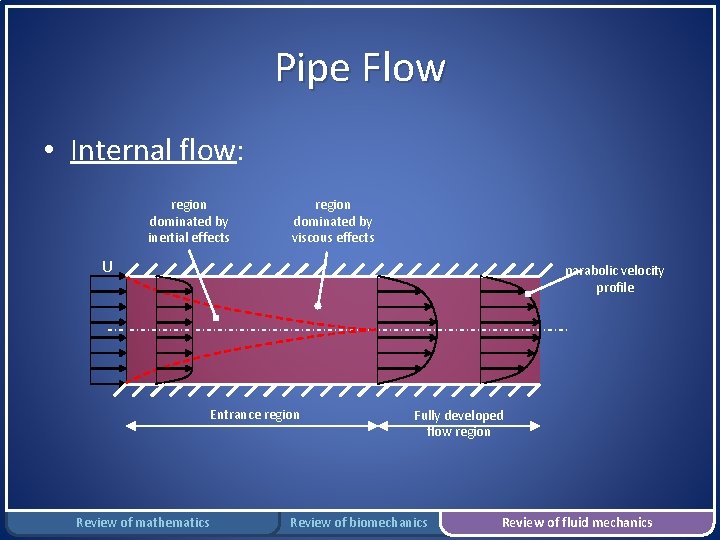
Pipe Flow • Internal flow: region dominated by inertial effects region dominated by viscous effects U parabolic velocity profile Entrance region Review of mathematics Fully developed flow region Review of biomechanics Review of fluid mechanics

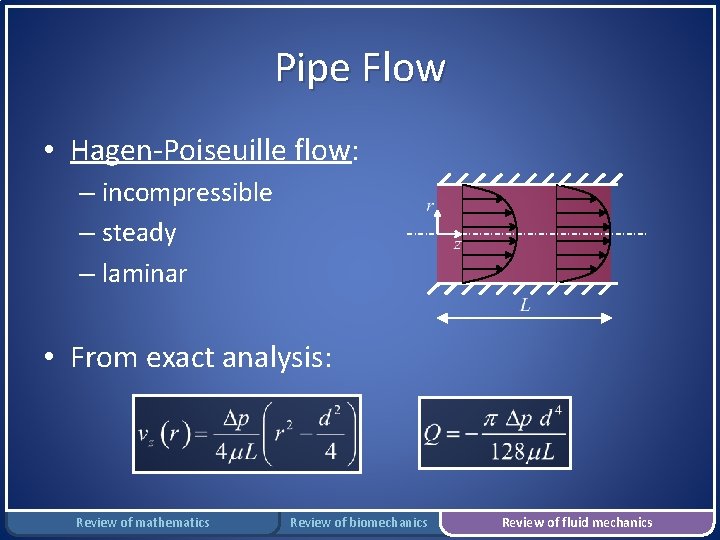
Pipe Flow • Hagen-Poiseuille flow: – incompressible – steady – laminar • From exact analysis: Review of mathematics Review of biomechanics Review of fluid mechanics

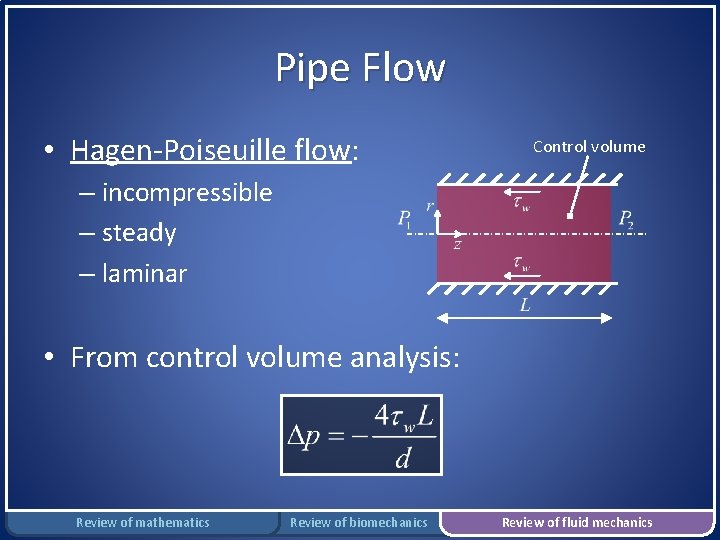
Pipe Flow • Hagen-Poiseuille flow: Control volume – incompressible – steady – laminar • From control volume analysis: Review of mathematics Review of biomechanics Review of fluid mechanics