ME 381 R Lecture 7 Phonon Scattering Thermal

ME 381 R Lecture 7: Phonon Scattering & Thermal Conductivity Dr. Li Shi Department of Mechanical Engineering The University of Texas at Austin, TX 78712 www. me. utexas. edu/~lishi@mail. utexas. edu • Reading: 1 -3 -3, 1 -6 -2 in Tien et al • References: Ch 5 in Kittel

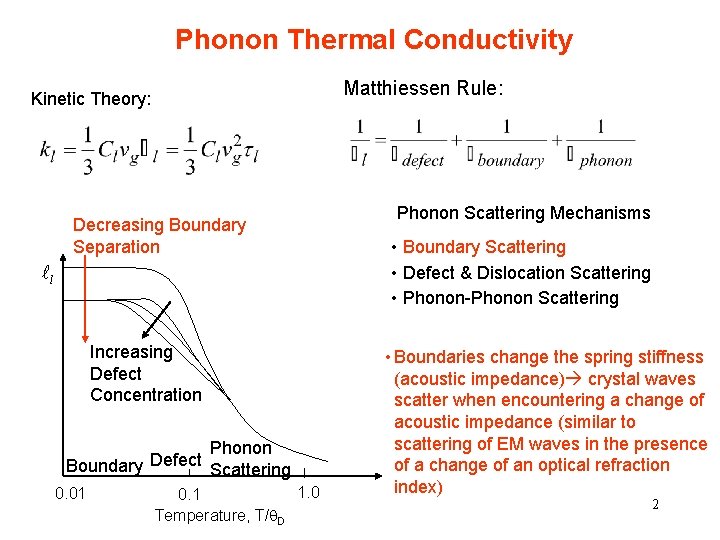
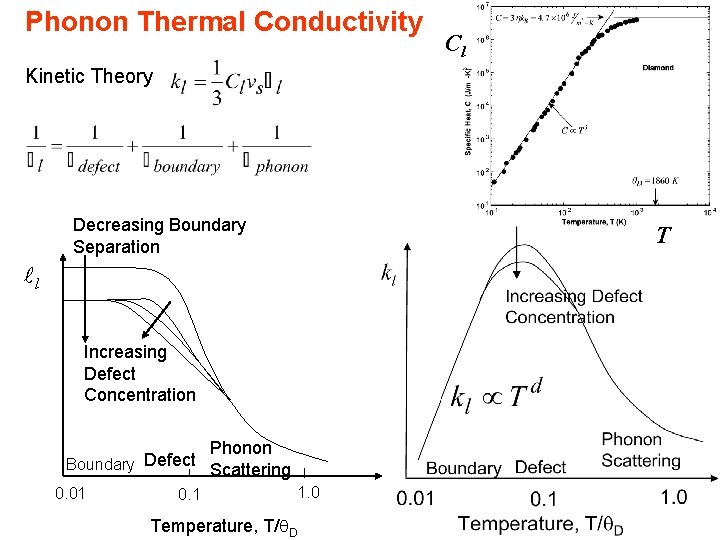
Phonon Thermal Conductivity Matthiessen Rule: Kinetic Theory: Decreasing Boundary Separation l Increasing Defect Concentration Phonon Defect Boundary Scattering 0. 01 1. 0 0. 1 Temperature, T/q. D Phonon Scattering Mechanisms • Boundary Scattering • Defect & Dislocation Scattering • Phonon-Phonon Scattering • Boundaries change the spring stiffness (acoustic impedance) crystal waves scatter when encountering a change of acoustic impedance (similar to scattering of EM waves in the presence of a change of an optical refraction index) 2

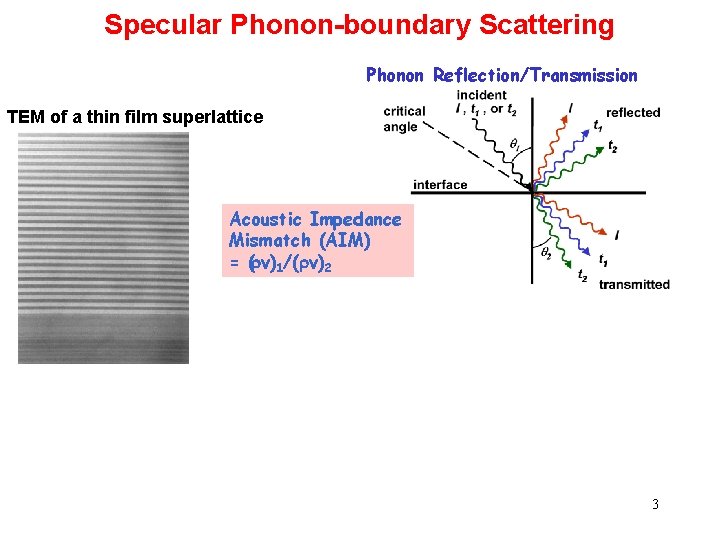
Specular Phonon-boundary Scattering Phonon Reflection/Transmission TEM of a thin film superlattice Acoustic Impedance Mismatch (AIM) = (rv) 1/(rv) 2 3

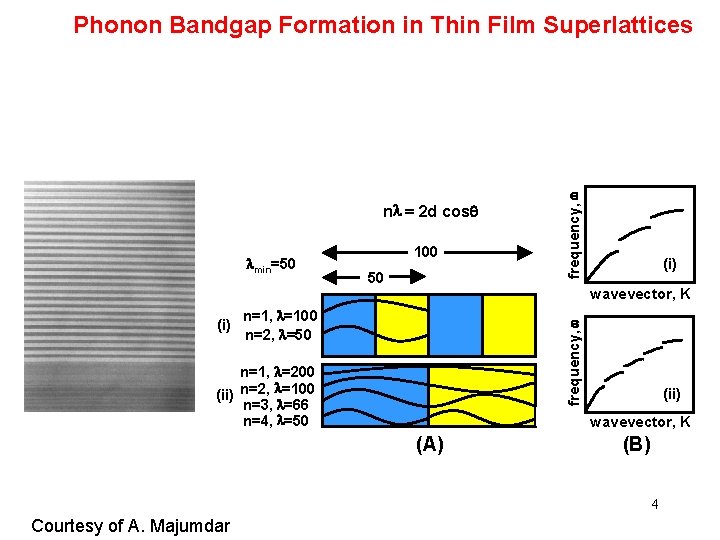
nl = 2 d cosq lmin=50 50 (i) wavevector, K n=1, l=100 n=2, l=50 frequency, w (i) 100 frequency, w Phonon Bandgap Formation in Thin Film Superlattices n=1, l=200 l (ii) n=2, =100 n=3, l=66 n=4, l=50 (ii) wavevector, K (A) (B) 4 Courtesy of A. Majumdar

Diffuse Phonon-boundary Scattering Specular Acoustic Mismatch Model (AMM) Khalatnikov (1952) Diffuse Mismatch Model (DMM) Swartz and Pohl (1989) E. Swartz and R. O. Pohl, “Thermal Boundary Resistance, ” Reviews of Modern Physics 61, 605 (1989). D. Cahill et al. , “Nanoscale thermal transport, ” J. Appl. Phys. 93, 793 (2003). 5 Courtesy of A. Majumdar

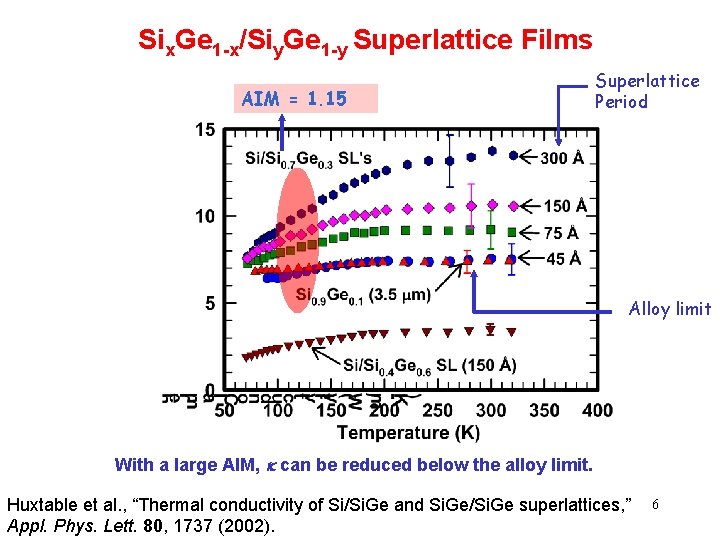
Six. Ge 1 -x/Siy. Ge 1 -y Superlattice Films AIM = 1. 15 Superlattice Period Alloy limit With a large AIM, k can be reduced below the alloy limit. Huxtable et al. , “Thermal conductivity of Si/Si. Ge and Si. Ge/Si. Ge superlattices, ” Appl. Phys. Lett. 80, 1737 (2002). 6

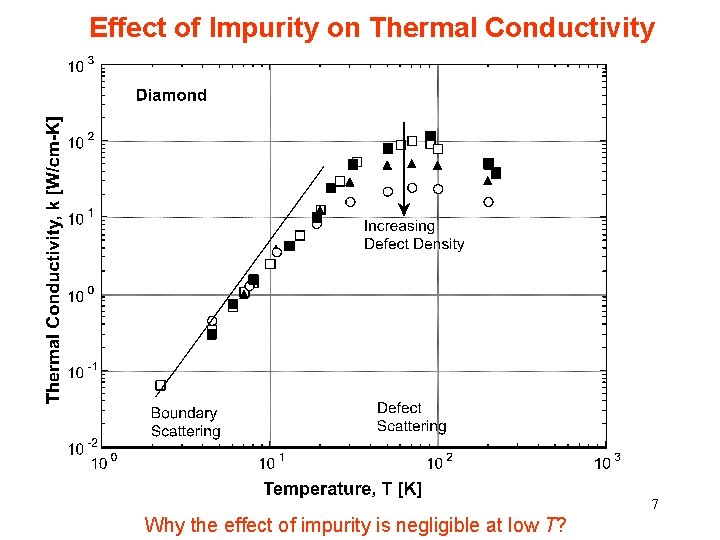
Effect of Impurity on Thermal Conductivity 7 Why the effect of impurity is negligible at low T?

Phonon-Impurity Scattering • Impurity change of M & C change of spring stiffness (acoustic impedance) crystal wave scatter when encountering a change of acoustic impedance (similar to scattering of EM wave in the presence of a change of an optical refraction index) • Scattering mean free time for phonon-impurity scattering: li ~ 1/(sr) where r is the impurity concentration, and the scattering cross section s = R 2 [ 4/( 4+1)] R: radius of lattice imperfaction l: phonon wavelength = 2 R/l -> 0: s ~ 4 (Rayleigh scatttering that is responsible for the blue sky and red sunset) -> : s ~ R 2 8

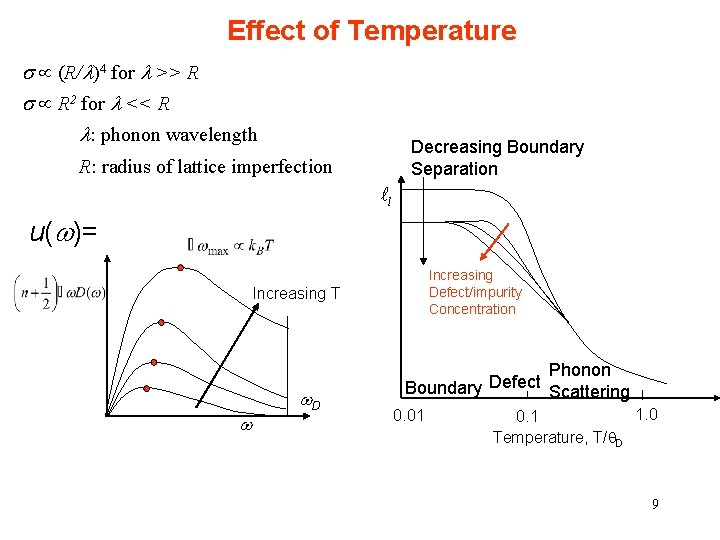
Effect of Temperature s (R/l)4 for l >> R s R 2 for l << R l: phonon wavelength Decreasing Boundary Separation R: radius of lattice imperfection l u(w)= Increasing Defect/impurity Concentration Increasing T w w. D Phonon Defect Boundary Scattering 0. 01 1. 0 0. 1 Temperature, T/q. D 9

k [W/m-K] Bulk Materials: Alloy Limit of Thermal Conductivity A Alloy Limit B Impurity and alloy atoms scatter only short- l phonons that are absent at 10 low T!

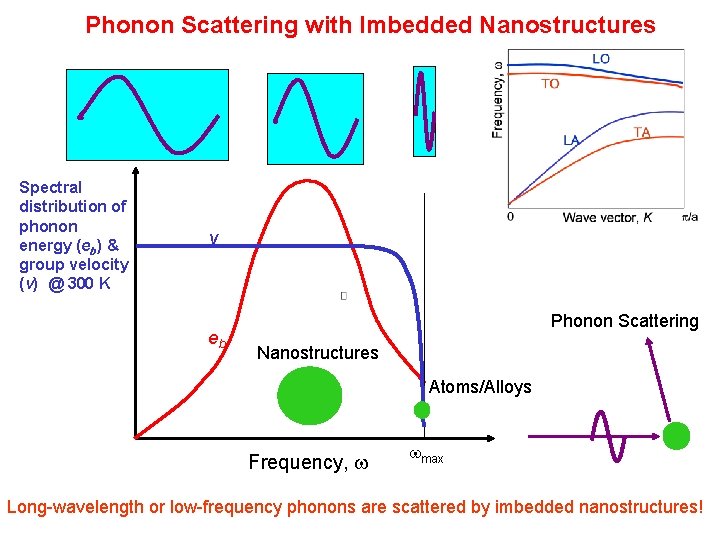
Phonon Scattering with Imbedded Nanostructures Spectral distribution of phonon energy (eb) & group velocity (v) @ 300 K v eb Phonon Scattering Nanostructures Atoms/Alloys Frequency, w wmax 11 Long-wavelength or low-frequency phonons are scattered by imbedded nanostructures!

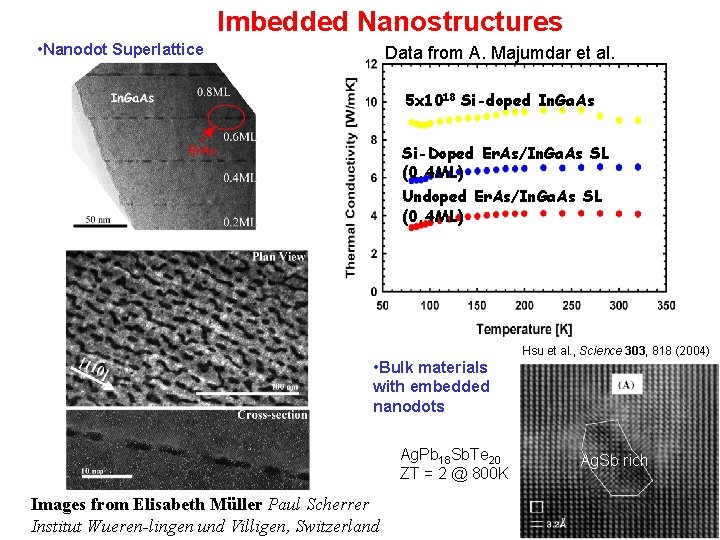
Imbedded Nanostructures • Nanodot Superlattice Data from A. Majumdar et al. 5 x 1018 Si-doped In. Ga. As Si-Doped Er. As/In. Ga. As SL (0. 4 ML) Undoped Er. As/In. Ga. As SL (0. 4 ML) Hsu et al. , Science 303, 818 (2004) • Bulk materials with embedded nanodots Ag. Pb 18 Sb. Te 20 ZT = 2 @ 800 K Images from Elisabeth Müller Paul Scherrer Institut Wueren-lingen und Villigen, Switzerland Ag. Sb rich 12

Phonon-Phonon Scattering • The presence of one phonon causes a periodic elastic strain which modulates in space and time the elastic constant (C) of the crystal. A second phonon sees the modulation of C and is scattered to produce a third phonon. • By scattering, two phonons can combine into one, or one phonon breaks into two. These are inelastic scattering processes (as in a non-linear spring), as opposed to the elastic process of a linear spring (harmonic oscillator). 13

Phonon-Phonon Scattering (Normal Process) Anharmonic Effects: Non-linear spring K 1 K 3 = K 1+K 2 Non-linear Wave Interaction Because the vectorial addition is the same as momentum conservation for particles: Phonon Momentum = K Momentum Conservation: K 3 = K 1+ K 2 Energy Conservation: w 3= w 1 + w 2 14

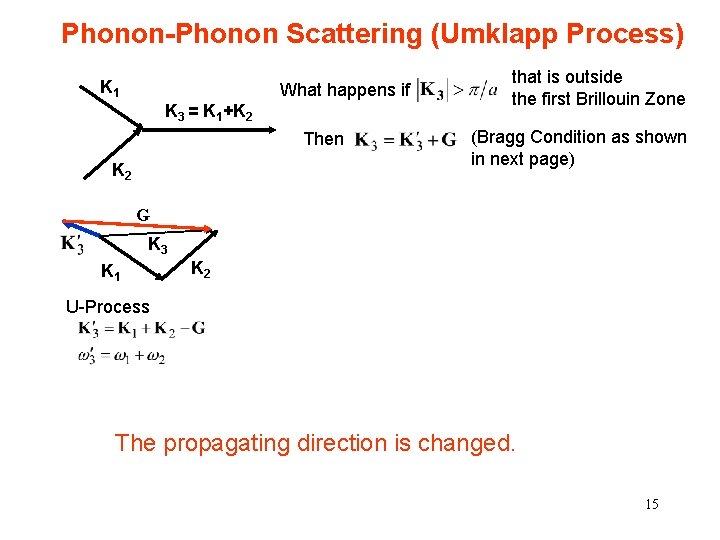
Phonon-Phonon Scattering (Umklapp Process) K 1 What happens if K 3 = K 1+K 2 Then K 2 that is outside the first Brillouin Zone (Bragg Condition as shown in next page) G K 3 K 1 K 2 U-Process The propagating direction is changed. 15

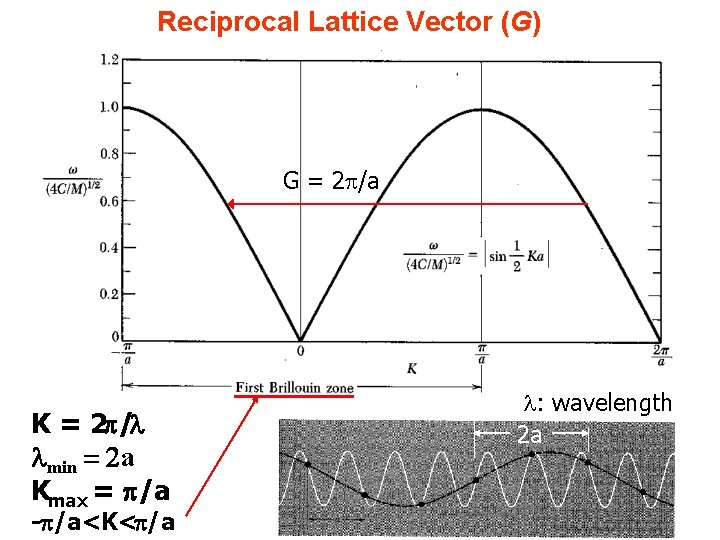
Reciprocal Lattice Vector (G) G = 2 p/a K = 2 /l lmin = 2 a Kmax = /a - /a<K< /a l: wavelength 2 a 16

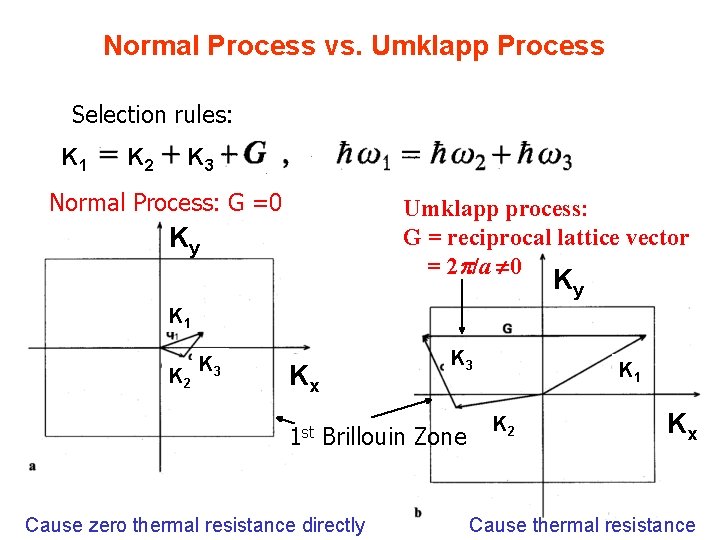
Normal Process vs. Umklapp Process Selection rules: K 1 K 2 K 3 Normal Process: G =0 Umklapp process: G = reciprocal lattice vector = 2 p/a 0 Ky Ky K 1 K 2 K 3 Kx 1 st Brillouin Zone K 1 Kx K 2 17 Cause zero thermal resistance directly Cause thermal resistance

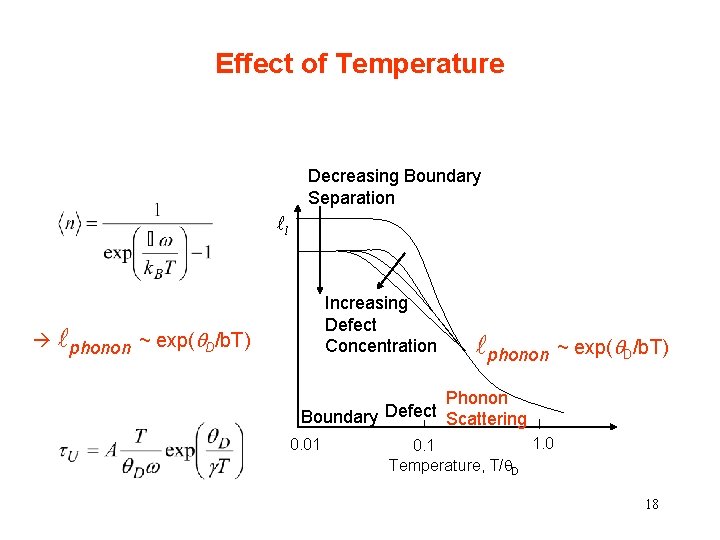
Effect of Temperature Decreasing Boundary Separation l Increasing Defect Concentration phonon ~ exp( D/b. T) Phonon Boundary Defect Scattering 0. 01 1. 0 0. 1 Temperature, T/q. D 18

Phonon Thermal Conductivity Cl Kinetic Theory Decreasing Boundary Separation T l Increasing Defect Concentration Phonon Defect Boundary Scattering 0. 01 0. 1 1. 0 Temperature, T/q. D

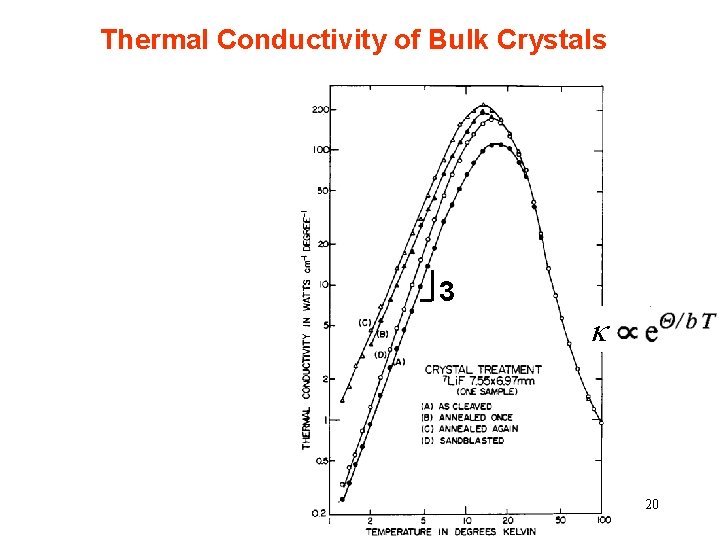
Thermal Conductivity of Bulk Crystals 3 k 20