MCS 680 Foundations Of Computer Science int MSTWeightint

MCS 680: Foundations Of Computer Science int MSTWeight(int graph[][], int size) { int i, j; int weight = 0; O(1) 1 n 1 for(i=0; i<size; i++) for(j=0; j<size; j++) n weight+= graph[i][j]; O(n) return weight; } O(n) O(1) Running Time = 2 O(1) + O(n 2) = O(n 2) Brian Mitchell http: //www. mcs. drexel. edu/~bmitchel email: bmitchel@mcs. drexel. edu Drexel University Fall 1997 Brian Mitchell (bmitchel@mcs. drexel. edu) - 1

Introduction • Instructor Brian Mitchell - “Brian” bmitchel@mcs. drexel. edu www. mcs. drexel. edu/~bmitchel (215)895 -2668 • Course Information Foundations of Computer Science (FCS) MCS 680 Section 510 Wednesday 6: 00 - 9: 00 PM Room Location: Curtis 250 A Office Hours By Appointment • Online Information www. mcs. drexel. edu/~bmitchel/course/mcs 680 -fcs Please check course web page several times per week. The web page will be my primary mechanism for communicating: Special and Emergency Information Syllabus Assignments Solutions to Problems Brian Mitchell (bmitchel@mcs. drexel. edu) - 2

Introduction • Course Objective – To provide a solid background in theoretical and mathematical aspects of Computer Science • Provide essential background knowledge that is required for success in other core computer science graduate courses • Textbook A. V. Aho, J. D. Ullman, Foundations of Computer Science, W. H. Freeman and Co. , 1995. • Additional References H. R. Lewis, C. H. Papadimitriou, Elements Of Theory Of Computation, Prentice Hall, 1981. T. H. Cormen, C. E. Leiserson & R. L. Rivest, Introduction To Algorithms, Mc. Graw Hill, 1996. Brian Mitchell (bmitchel@mcs. drexel. edu) - 3

Introduction • Homework, Exams Assignments & Programming Projects: Homework sets consisting of 4 -5 problems will be regularly assigned (consult web page). Based on difficulty, you will have 1 -2 weeks to complete each assignment. Some assignments might require you to write a small program or a program fragment. For this course you may develop programming solutions using the ‘C’, ‘C++’ or Java programming languages Midterm: A 90 minute midterm exam will be given during the 5 th or 6 th week of the course. Final: A 2 hour final exam will be given during our regularly scheduled class time on finals week. Brian Mitchell (bmitchel@mcs. drexel. edu) - 4

Introduction • Grading – The following distribution will be used to determine your final grade in this course: • 50%: Homework & Programming Projects • 20%: Midterm Exam • 30%: Final Exam • Policies – All homework and programming assignments are individual efforts, unless specifically stated otherwise in the assignment definition. • You may use your colleagues for advice, however, all assignments must be your original work – Late assignments will be penalized 10% per week. Any assignment not submitted within 2 weeks of the deadline will not be accepted unless you work out special arrangements with me. Brian Mitchell (bmitchel@mcs. drexel. edu) - 5

Introduction • Tentative List Of Topics – – – – Summation and Logarithm Review Ineration, Induction & Recursion Big-Oh Analysis Running Time Recurrence Relations Trees (Mathematical Aspects & Algorithms) Sets Graph Theory & Graph Algorithms Relations Automata Regular Expressions Context Free Grammars Propositional Logic Predicate Logic Brian Mitchell (bmitchel@mcs. drexel. edu) - 6

Summations • Algorithms often contain an interative control construct – Loops (while, for, do…while) – Algorithm analysis can be performed by examining the sum of the times spent on each execution of the loop – Example: What is the value of i? int i; for (i=1; i<=n; i++) { i += i; } n j = 1+2+…+(n-1)+n j=1 Brian Mitchell (bmitchel@mcs. drexel. edu) - 7

Summations • Properties of sums j=1 n aj = lim n a j j=1 If the limit does not exist, the sum diverges; otherwise, it converges. n n n ca + db = c a j j j b + d j=1 j=1 Summations obey the linearity property Brian Mitchell (bmitchel@mcs. drexel. edu) - j 8

Common Summations n n(n+1) j = 2 j=1 n n+1 - 1 x xj = x-1 j=0 n a -a j j-1 = a n - a 0 j=1 n-1 a -a j j+1 = a 0 - an j=0 n c = n • c j=1 Brian Mitchell (bmitchel@mcs. drexel. edu) - 9

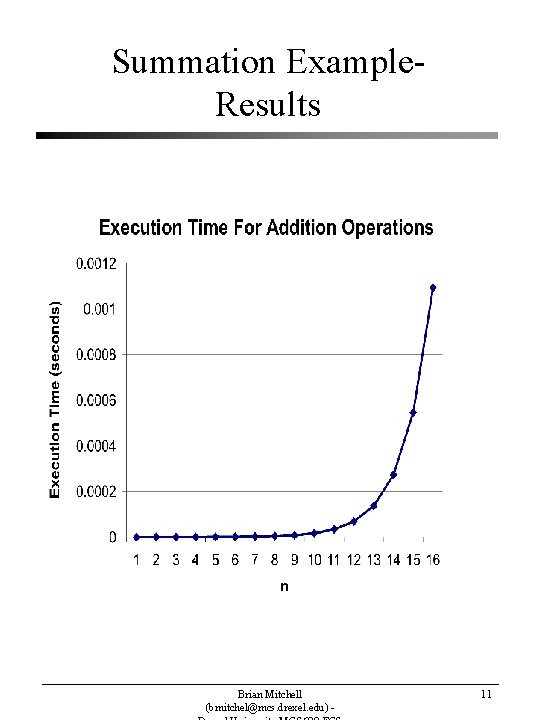
Summation Example • Consider: int foo(int n) { int i, j, k; for (i=1; i<=n; i++) for(j=1; j<=n; j++) k += i + j; } How much time is spent performing the addition operations in the above code fragment if an add operation takes 2 clock cycles on a Pentium 120 Mhz microprocessor? n n n add. Ops = i=1 j=1 n • add. Ops i=1 = n 2 • add. Ops On a 120 Mhz microprocessor each clock cycle takes 8. 3333 ns. (10 -9 seconds). Thus the total amount of time the code fragement spends adding is: = n 2 • (2 • 8. 3333 E-9) = 16. 667 n 2 ns. Brian Mitchell (bmitchel@mcs. drexel. edu) - 10

Summation Example. Results Brian Mitchell (bmitchel@mcs. drexel. edu) - 11

Summation Example What is the value of k? int foo(int n) { int i, j, k; for (i=1; i<=n; i++) for(j=1; j<=n; j++) k += (i + j); } Brian Mitchell (bmitchel@mcs. drexel. edu) - 12

Summation Example What is the value of k? int foo(int n) { int i, j, k; for (i=1; i<=n; i++) for(j=1; j<=i; j++) k += (i + j); } Brian Mitchell (bmitchel@mcs. drexel. edu) - 13

Logarithms • Logarithms appear often during the analysis of algorithms – General form: logb x • b is the base of the logarithm • if b is not specified then 10 is assumed – Definition: The logarithm to the base b of x represents the power to which b must be raised to produce x – Examples: log 2 8 = 3 (since 23 = 8) log 3 81 = 4 (since 34 = 81) log 10 1 = 0 (since 100 = 1) – During the analysis of algorithms, log 2 x appears often • We will use lg x to represent log 2 x Brian Mitchell (bmitchel@mcs. drexel. edu) - 14

Logarithms • Notation – lg n = log 2 n = (log n / log 2) – ln n = loge n • Identities – – – logb 1 = 0 logbk n = (logb n)k logb n = logb (logb n) logb (a/c) = logb a - logb c logb n = (1/ logn b) logc n = (logarb n / logarb c) - c is any base logb (1/n) = - logb nr = r logb nj = logb n + logb j a = blogb a alogb n = nlogb a Brian Mitchell (bmitchel@mcs. drexel. edu) - 15

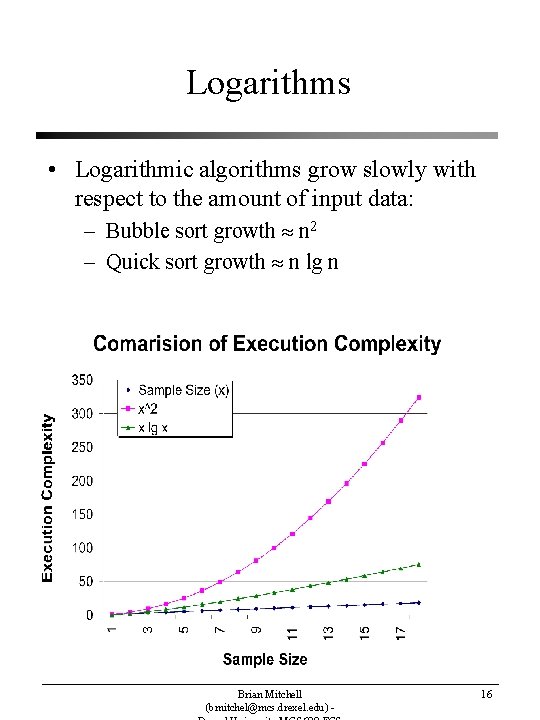
Logarithms • Logarithmic algorithms grow slowly with respect to the amount of input data: – Bubble sort growth n 2 – Quick sort growth n lg n Brian Mitchell (bmitchel@mcs. drexel. edu) - 16

Data Models, Data Structures & Algorithms • Data Models – Abstractions used to formulate problems – Any mathematical concept can be treated as a data model • Values that the data objects can assume • Operations on the data – Programming languages (‘C/C++’, Pascal, Java. . . ) support primitive data models • Integers, floating point, strings, chars, . . . • Operations: +, -, /, *, %, <, >, <=, >=, ==. . . • However there are other important data models – Sets, graphs, trees, expressions – These data models are mathematically understood, however, most programming languages do not provide intrinsic support Brian Mitchell (bmitchel@mcs. drexel. edu) - 17

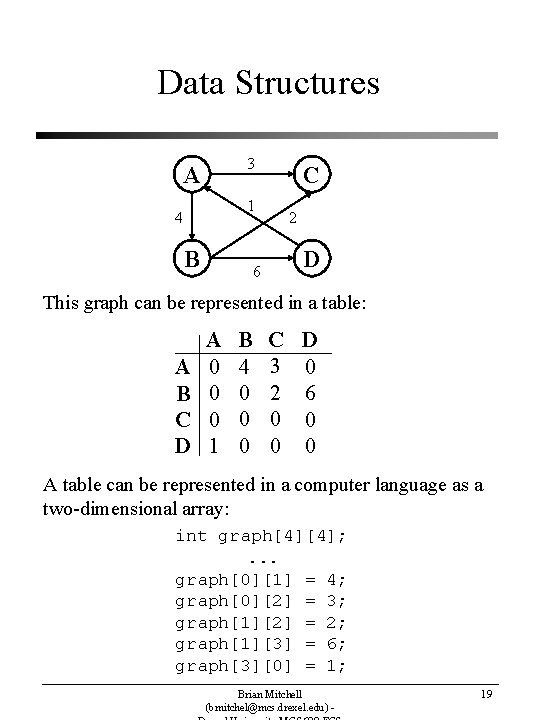
Data Models, Data Structures & Algorithms • Data Structures • Most programming languages do not directly support important data models – Must represent the needed data model by using abstractions that are supported by the language • Data structures are methods for representing a data model in a programming language • Consider the following weighted and directed graph: A C B D Brian Mitchell (bmitchel@mcs. drexel. edu) - 18

Data Structures 3 A C 1 4 B 2 D 6 This graph can be represented in a table: A B C D A 0 0 0 1 B 4 0 0 0 C 3 2 0 0 D 0 6 0 0 A table can be represented in a computer language as a two-dimensional array: int graph[4][4]; . . . graph[0][1] = 4; graph[0][2] = 3; graph[1][2] = 2; graph[1][3] = 6; graph[3][0] = 1; Brian Mitchell (bmitchel@mcs. drexel. edu) - 19

Algorithms • Precise an unambiguous specification of a sequence of steps that can be carried out automatically • In Computer Science, algorithms are expressed using programming languages • Consider an algorithm for calculating the total weight of a graph. – Our data structure is a two-dimensional graph int Graph. Weight(int graph[][], int size) { int i, j, weight; weight = 0; for(i=0; i<size; i++) for(j=0; j<size; j++) weight+= graph[i][j]; return weight; } Brian Mitchell (bmitchel@mcs. drexel. edu) - 20

Running Times Of Algorithms • Desire to analyze algorithm running time • Used to determine how “good” an algorithm performs – – – Inputs of various sizes Best Case Worst Case Average Case Bounding Performance • We use “Big-Oh” analysis to model running time (also known as execution complexity) – – – O(n) O(n 2) O(2 n) O(n log n) O(n lg n) Brian Mitchell (bmitchel@mcs. drexel. edu) - 21