MCA 202 Discrete Structures Instructor Neelima Gupta nguptacs







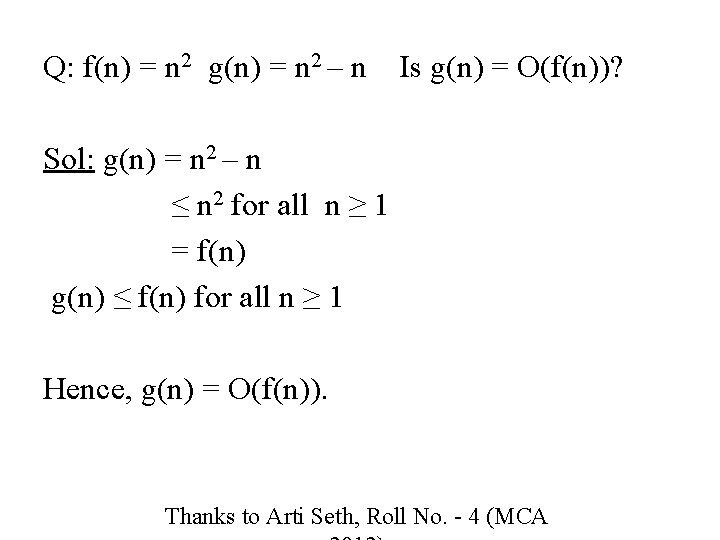
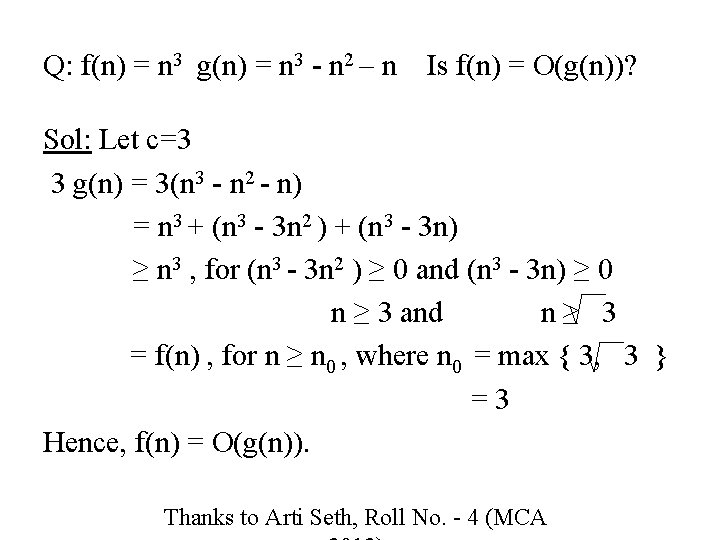



















- Slides: 30

MCA 202: Discrete Structures Instructor Neelima Gupta ngupta@cs. du. ac. in

Table Of Contents Growth Functions

Introduction • For each problem to be solved, we may have multiple algorithms as solution. However, the best must be chosen. • Comparison of the algorithms depends mainly on: – Time Complexity Time the algorithm takes to run. – Memory Space Memory the algorithm requires. Thanks to Arti Seth, Roll No. - 4 (MCA

• Let us consider two algorithms for a same problem that run in f 1(n) and f 2(n) respectively, ‘n’ being the input size (memory words required for inputs). • Consider the graph for f 1(n) and f 2(n). For smaller values (n<n 0), we don’t care, however we observe that for larger values of n (n n 0), f 1(n) f 2(n), i. e, f 1(n) grows slower than f 2(n). Hence, we should prefer f 1(n). f 2(n )f ( 1 n) no Thanks to Arti Seth, Roll No. - 4 (MCA

Asymptotic Notations Big O Notation • In general a function – f(n) is O(g(n)) if there exist positive constants c and n 0 such that f(n) c g(n) for all n n 0 • Formally – O(g(n)) = { f(n): positive constants c and n 0 such that f(n) c g(n) n n 0 • Intuitively, it means f(n) grows no faster than g(n). Thanks to Arti Seth, Roll No. - 4 (MCA

Examples: Q: f(n) = n 2 g(n) = n 2 – n Is f(n) = O(g(n))? Sol 1: (by hit and trial method) Let c = 1 Claim: n 2 1(n 2 -n) Proof: To show: n 2<=n(n-1) T. S: n n-1, which is not true for any value of n. Let c = 2 Claim: n 2 2(n 2 -n) Proof: T. S: n 2 2 n 2 -2 n T. S: 2 n n 2, which is true for n 2. Hence, f(n) = O(g(n)) Thanks to Arti Seth, Roll No. - 4 (MCA

Sol 2: Let c = 2, 2 g(n) = 2(n 2 -n) = n 2 + (n 2 -2 n) n 2 , for n 2 -2 n 0 n 2 2 n n 2 = f(n) Hence, f(n) = O(g(n)). • If power and coefficient of leading terms of f(n) and g(n) are same, then for simplicity ‘c’ can be taken as: c = Number of negative terms + 1 Thanks to Arti Seth, Roll No. - 4 (MCA
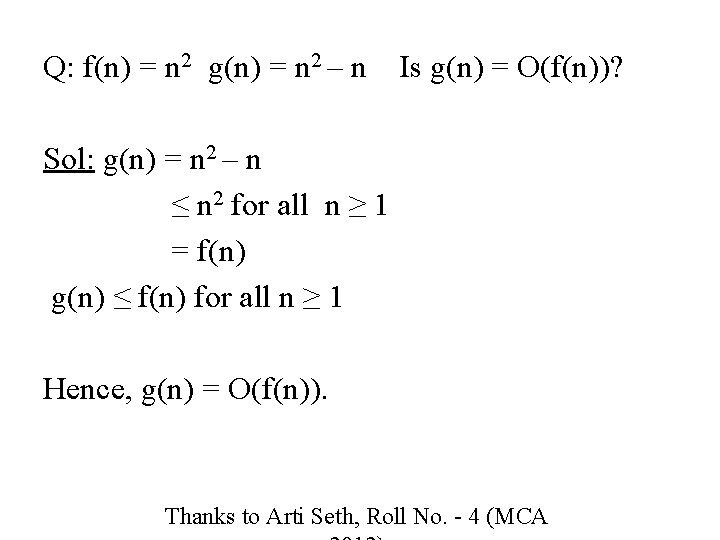
Q: f(n) = n 2 g(n) = n 2 – n Is g(n) = O(f(n))? Sol: g(n) = n 2 – n ≤ n 2 for all n ≥ 1 = f(n) g(n) ≤ f(n) for all n ≥ 1 Hence, g(n) = O(f(n)). Thanks to Arti Seth, Roll No. - 4 (MCA
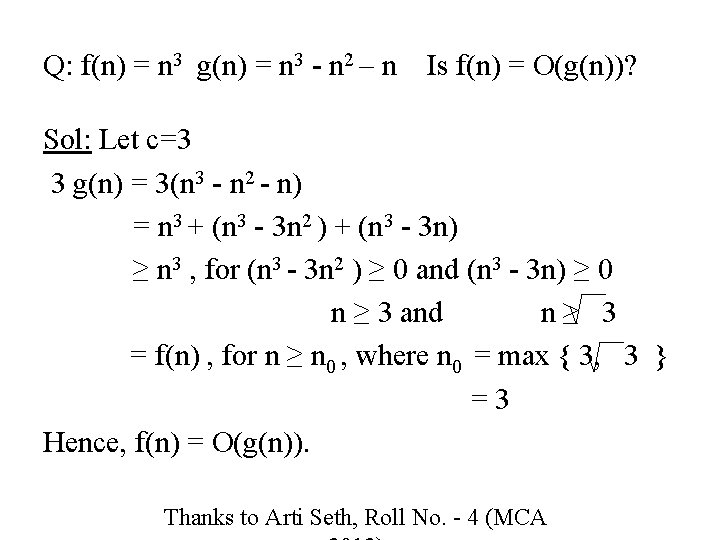
Q: f(n) = n 3 g(n) = n 3 - n 2 – n Is f(n) = O(g(n))? Sol: Let c=3 3 g(n) = 3(n 3 - n 2 - n) = n 3 + (n 3 - 3 n 2 ) + (n 3 - 3 n) ≥ n 3 , for (n 3 - 3 n 2 ) ≥ 0 and (n 3 - 3 n) ≥ 0 n ≥ 3 and n≥ 3 = f(n) , for n ≥ n 0 , where n 0 = max { 3, 3 } =3 Hence, f(n) = O(g(n)). Thanks to Arti Seth, Roll No. - 4 (MCA

Q: f(n) = n 3 g(n) = n 3 - n 2 – n Is g(n) = O(f(n))? Sol: g(n) = n 3 - n 2 – n ≤ n 3 for all n ≥ 1 = f(n) g(n) ≤ f(n) for all n ≥ 1 Hence, g(n) = O(f(n)). Thanks to Arti Seth, Roll No. - 4 (MCA

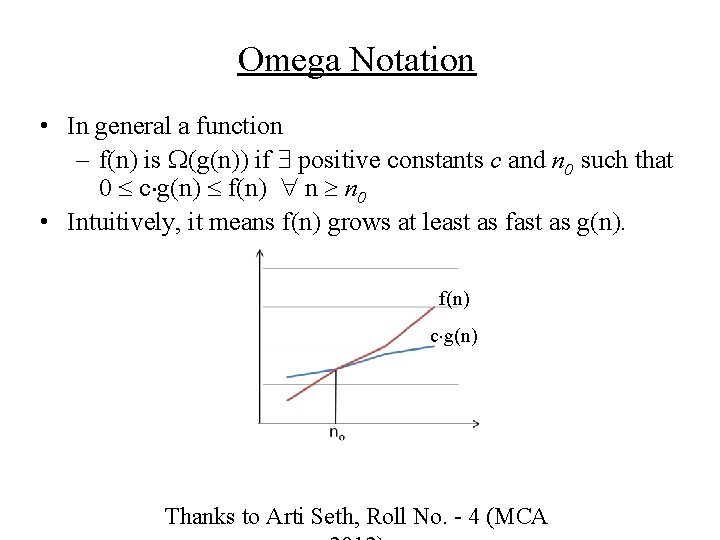
Omega Notation • In general a function – f(n) is (g(n)) if positive constants c and n 0 such that 0 c g(n) f(n) n n 0 • Intuitively, it means f(n) grows at least as fast as g(n). f(n) c g(n) Thanks to Arti Seth, Roll No. - 4 (MCA

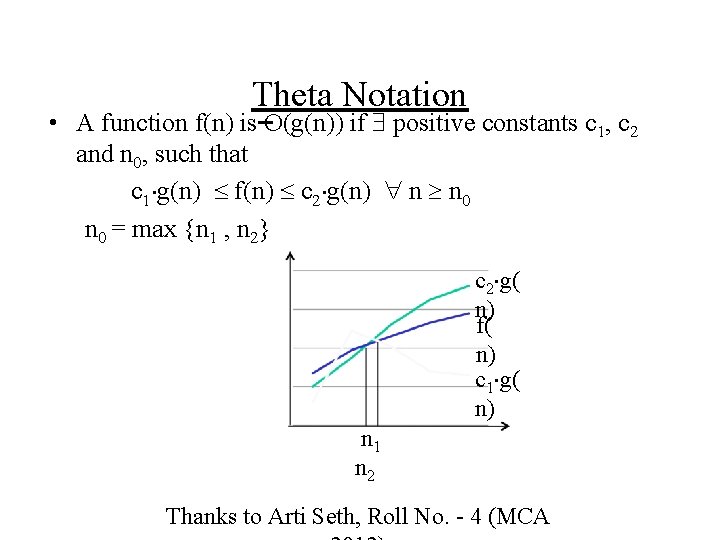
Theta Notation • A function f(n) is O(g(n)) if positive constants c 1, c 2 and n 0, such that c 1 g(n) f(n) c 2 g(n) n n 0 = max {n 1 , n 2} c 2 g( n) f( n) c 1 g( n) n 1 n 2 Thanks to Arti Seth, Roll No. - 4 (MCA

f(n) g(n) c n 3+ n 2 -10 n+5 f(n)=O(g(n)) >=1 n 3 - 2 n 2 + 100 n F(n)=O(g(n)) >1 n 5+ 4 n 4 - 3 n 3+ 2 n 2 – n +1 F(n)=Ω (g(n)) <1 n 5 - 4 n 4 + 3 n 3 - 2 n 2 + n -1 F(n)=Ω (g(n)) <=1 Thanks Anika Garg Roll no. -1 MCA 2012

Assignment 0: Relations Between , , O For any two functions g(n) and f(n), f(n) = (g(n)) iff f(n) = O(g(n)) and f(n) = (g(n)).

Assignment No 1 • Self study a 0 + a 1 + … + an = (an+1 - 1)/(a - 1) for all a 1 – What is the sum for a = 2/3 as n infinity? Is it O(1)? Is it big or small? – For a = 2, is the sum = O(2^n)? Is it big or small? Q 1 Show that a polynomial of degree k = theta(n^k).

Other Asymptotic Notations • A function f(n) is o(g(n)) if for every positive constant c, there exists a constant n 0 > 0 such that f(n) < c g(n) n n 0 • A function f(n) is (g(n)) if for every positive constant c, there exists a constant n 0 > 0 such that c g(n) < f(n) n n 0 • Intuitively, – () is like > – () is like = – o() is like < – () is like – O() is like

Arrange some functions • f(n) = O(g(n)) => f(n) = o(g(n)) ? • Is the converse true? • Let us arrange the following functions in ascending order (assume log n = o(n) is known) – n, n^2, n^3, sqrt(n), n^epsilon, log^2 n, n log n, n/log n, 2^n, 3^n

Relation between n & 2 n Intuitively, n appears to be smaller than n 2. Lets prove it now. T. P. For any constant c > 0 n < c n 2 i. e. 1 < c n i. e. n > 1 / c Hence, n < c n 2 for n > 1 / c i. e. n = o( n 2) we can also write it as n < n 2.

Relation between n 2 & n 3 Intuitively, n 2 appears to be smaller than n 3. Lets prove it now. T. P. For any constant c > 0 n 2 < c n 3 i. e. 1 < c n i. e. n > 1 / c Hence, n 2 < c n 3 for n > 1 / c i. e. n 2 = o( n 3) we can also write it as n 2 < n 3.

Relation between n & n 1/2 Since n = o (n 2 ), we have, For every constant c > 0, there exists n_c s. t. n < c n 2 for all n >= n_c Thus sqrt(n) < c n for all sqrt(n) >= n_c i. e. sqrt(n) < c n for all n >= n_c^2. Thus, n 1/2 = o( n) we can also write it as n 1/2 < n. Combining the previous result n 1/2 < n 3

Relation between n & log n • For the time being we can assume the result log ( n ) = o(n) Þ log ( n ) < n we will prove it later.

Relation between n 1/2 & log n Assume log n = o(n) let c > 0 be any constant for c/2 > 0 there exists m > 0 such that log n < (c/2) n for n > m changing variables from n to n 1/2 we get log(n 1/2 ) < (c/2) n 1/2 for n 1/2 > m ½ log( n ) < (c/2) n 1/2 for n > m 2

Contd. . let m 2 = k log( n ) < c n 1/2 for n > k Since c > 0 was chosen arbitrarily hence log n = o( n 1/2 ) or log n < n 1/2 Combining the results we get log n < n 1/2 < n 3

Relation between 2 n & nlog n • Since log n = o(n) for c > 0, n 0 > 0 such that n n 0, we have log n < c n Multiplying by n on both sides we get n log( n ) < c n 2 n n 0 Þ nlog n = o( n 2 ) Þ nlog n < n 2

Relation between n & nlog n Solution: let c> 0 be any constant such that n < c n log (n) Þ 1 < c log( n ) Þ log( n) > 1 / c Þ n > e 1/c i. e. n < c n log n n > e 1/c Since c was chosen arbitrarily n = o( n log n ) or n < n log n Combining the results we can get log n < n 1/2 < n logn < n 2 < n 3

Relation between n & n/log n • We know that n = o(nlogn) for c > 0, n 0 > 0 such that n n 0, we have n < c n log n dividing both sides by log n we get n/ log( n) < c n n n 0 Þ n / logn = o(n) i. e. n / logn < n

Assignment No 2 • Show that log^M n = o(n^epsilon) for all constants M>0 and epsilon > 0. Assume that log n = o(n). Also prove the following Corollary: log n = o(n/log n) • Show that n^epsilon = o(n/logn ) for every 0 < epsilon < 1.

Hence we have, log n < n/log n < n 1/2 < n logn < n 2 < n 3

Assignment No 3 • Show that – lim f(n)/g(n) = 0 => f(n) = o(g(n)). n→∞ – lim f(n)/g(n) = c => f(n) = θ(g(n)). n → ∞, where c is a positive constant. • Show that log n = o(n). • Show that n^k = o(2^n) for every positive constant k.

• Show by definition of ‘small o’ that a^n = o(b^n) whenever a < b , a and b are positive constants. Hence we have, log n < n/log n < n 1/2 < n logn < n 2 < n 3 <2 n < 3 n