MBAD 6122 Decision Modeling and Analysis via Spreadsheets

MBAD 6122 Decision Modeling and Analysis via Spreadsheets Dr. Cem Saydam Friday Building 266 B saydam@uncc. edu 1

Outline u Introductions u Course objectives - syllabus u Intro to Management Science - Chap. 1 u Intro to Optimization and LP - Chap. 2 u Modeling and solving LP problems via spreadsheets 2

Management Science u. Management Science (a. k. a. “analytics”) analytics is the scientific approach to decision making. u. Mgt. Sci. uses mathematical models to make sound decisions. http: //www. youtube. com/watch? v=Mdll. Rsh 0 z. Eg u http: //www. youtube. com/watch? v=3 bs. St. Zg. Ib_s&NR=1 u u The focal point of analysis is the problem and mathematical (quantitative) models are the vehicles by which solutions are obtained. u Mgt. Science uses a systematic and logical approach to problem solving. 3

Models u A model is an abstraction of reality. Models can be: ð Prescriptive functional relationships are well-known ð solutions prescribe (advise, recommend) a set of values for the decision variables in order to maximize (or minimize) an objective ð ð Predictive explanatory variables affect the outcome(s) ð functional relationship can be derived ð ð Descriptive describe the outcome or behavior of a system ð functional relationships might be well-known but are either too complex to tackle analytically or are highly stochastic ð 4

Mathematical Programming (MP) Bu t pro there gra mm is no req ing uir ed u MP, a. k. a. optimization, is a field of management science that finds the optimal, or most efficient, way of using limited resources to achieve the objectives of an individual or a business. u Is this part of “analytics”? What is “analytics”? u http: //www. sas. com/news/sascom/analytics_levels. pdf Source: Analytics: The art and science of better/Computer. World 5

General form of an Math Prog. Model u Every optimization problem involves the following: ü decisions that must be made ü objective(s) (or goal(s)) ü a set of restrictions (or constraints) MAX (or MIN): Subject to: f 0(X 1, X 2, …, Xn) f 1(X 1, X 2, …, Xn) <= b 1 : fk(X 1, X 2, …, Xn) >= bk : fm(X 1, X 2, …, Xn) = bm Note: If all the functions in an optimization are linear(ized), the problem is a Linear Programming (LP) problem 6

Intro to LP èAn example: Blue Ridge Hot Tubs, Inc. Blue Ridge Hot Tubs produces two types of hot tubs: Aqua-Spas & Hydro-Luxes. Pumps Labor Tubing Unit Profit Aqua-Spa 1 9 hours 12 feet $350 Hydro-Lux 1 6 hours 16 feet $300 There are 200 pumps, 1566 hours of labor, and 2880 feet of tubing available. 7

Formulating LP Models u Given a problem, first, determine the objective or goal. Maximize (or minimize) what? Maximize profits v Identify & define the decision variables (unknowns). u What should they represent and how many do we need? X 1=number of Aqua-Spas to produce X 2=number of Hydro-Luxes to produce or abbreviate as follows Xi = no. of product i to make i=1, 2 w State the objective as a linear function of the decision variables. Max 350 X 1 + 300 X 2 8

Formulating LP Models x Translate the requirements, restrictions, or wishes, that are in narrative form to linear functions. 1 X 1 + 1 X 2 <= 200 9 X 1 + 6 X 2 <= 1566 12 X 1 + 16 X 2 <= 2880 } pumps } labor } tubing y Identify any lower or upper bounds on the decision variables (non-negativity constraints are v. common). X 1 >= 0 X 2 >= 0 or Xi >= 0 i=1, 2 9

The Complete LP Model MAX: 350 X 1 + 300 X 2 S. T. : 1 X 1 + 1 X 2 <= 200 9 X 1 + 6 X 2 <= 1566 12 X 1 + 16 X 2 <= 2880 X 1 , X 2 >= 0 The general form of an LP model: MAX (or MIN): c 1 X 1 + c 2 X 2 + … + cn. Xn Subject to: a 11 X 1 + a 12 X 2 + … + a 1 n. Xn <= b 1 : ak 1 X 1 + ak 2 X 2 + … + akn. Xn >= bk : am 1 X 1 + am 2 X 2 + … + amn. Xn = bm 10

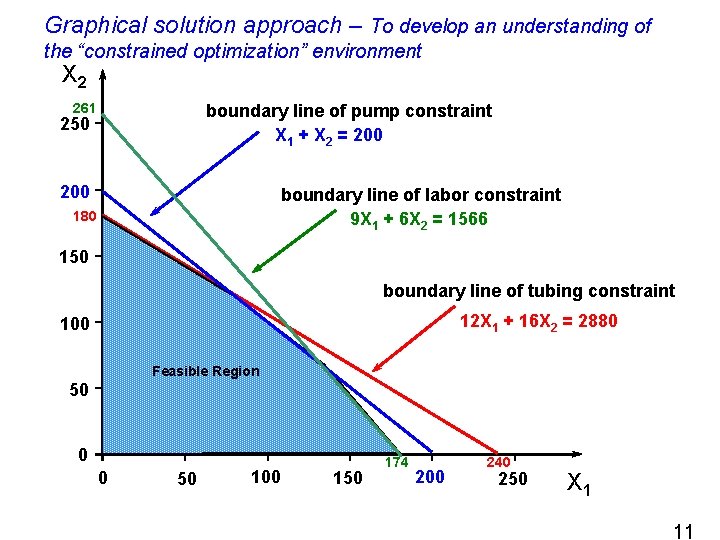
Graphical solution approach – To develop an understanding of the “constrained optimization” environment X 2 261 boundary line of pump constraint X 1 + X 2 = 200 250 200 boundary line of labor constraint 9 X 1 + 6 X 2 = 1566 180 150 boundary line of tubing constraint 12 X 1 + 16 X 2 = 2880 100 Feasible Region 50 0 0 50 100 150 174 200 240 250 X 1 11

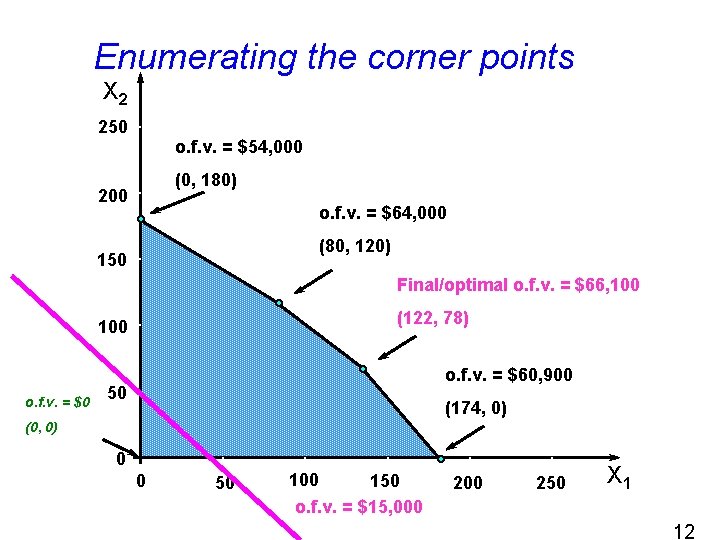
Enumerating the corner points X 2 250 o. f. v. = $54, 000 (0, 180) 200 o. f. v. = $64, 000 (80, 120) 150 Final/optimal o. f. v. = $66, 100 (122, 78) 100 o. f. v. = $60, 900 50 (174, 0) (0, 0) 0 0 50 100 150 o. f. v. = $15, 000 250 X 1 12

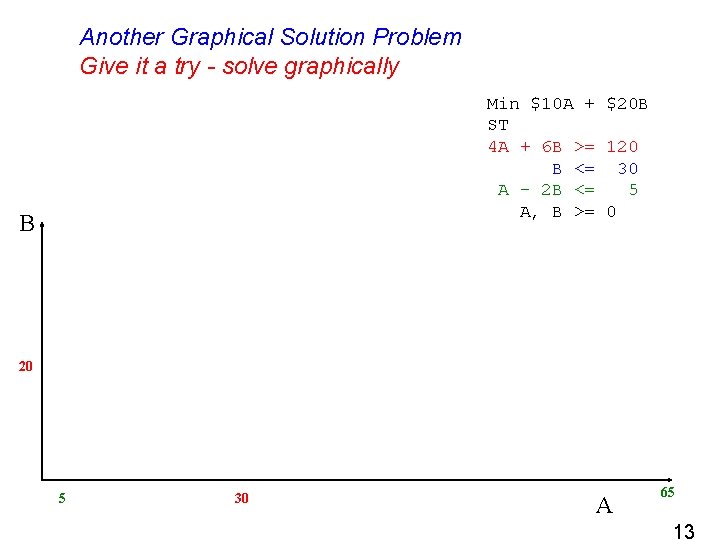
Another Graphical Solution Problem Give it a try - solve graphically Min $10 A + $20 B ST 4 A + 6 B >= 120 B <= 30 A - 2 B <= 5 A, B >= 0 B 20 5 30 A 65 13

Excel 2007 Standard Solver “Add-In” 14

Excel 2010 Standard Solver “Add-In” 15

How Excel 2007 standard solver views the model u Target cell - the cell in the spreadsheet that represents the objective function u Changing cells - the cells in the spreadsheet representing the decision variables u Constraint cells - the cells in the spreadsheet representing the LHS formulas on the constraints u Click on Options and check “Assume Linear Model” and “Assume Non-negative”, then, click OK, then click Solve! 16

How Excel 2010 standard solver views the model u Target cell - the cell in the spreadsheet that represents the objective function u Changing cells - the cells in the spreadsheet representing the decision variables u Constraints - the cells in the spreadsheet representing the LHS formulas on the constraints and the RHS values (could be formulas also but should not include decision variables in them. ) u For non-negativity constraints check and for Linear models select “Simplex LP” then, click OK, then click Solve! 17

Expanded Blue Ridge Hot Tubs Problem u BRHT has added another product line: Deck-Spa u Each Deck-Spa uses 1 pump, 7 hours of labor and 14 ft. of tubing. u Profit margin is estimated as $315/unit. 1. Expand the formulation 2. Setup in Excel and solve via solver 3. Interpret the solution What is the product mix? u What is the optimal profit (objective function)? u Other “observations” from investigating the solution provided by solver. u 18

Another Starter Formulation Exercise u The Pyrotec Company produces three electrical products clocks, radios, and toasters. The products have the following resource requirements: Product Cost/Unit Labor hours/Unit Clock $7 2 Radio 10 3 Toaster 5 2 u The manufacturer has a daily budget of $2, 000 and a maximum of 660 hours of labor. Maximum daily demand for radios is 300. The marketing department requires that at least 15 percent of the total products must be toasters. Clocks sell for $15, radios for $20, and toasters for $12. u Formulate as an LP. u Solve using solver. 19

Can we be so lucky, every time? u When we attempt to solve an LP, one of the following will occur: ü Unique optimal solution ü Multiple (alternate) optimal solutions Ð Unbounded solutions Ð Infeasible solution 20

Unbounded solutions u Always result of an error; a typo, misspecification etc. u Example: Max 3 x 1 + 5 x 2 ST x 1 + x 2 >= 100 x 1 <= 40 x 1, x 2 >= 0 21

Infeasible solution u Suppose the Pyrotec Co. problem has the following additional requirement: Management wants at least 350 Clocks. u Therefore we need to add one more constraint: u x 1 >= 350 u 22

Quick Practice (prior to Chap. 3) u Two practice problems from Chap 3: #22 (#19 in the 5 th ed. ) u #24 (#21 in the 5 th ed. ) u u Formulate u Setup and Solve using the standard solver in 2007 or 2010 u Install Risk Solver Platform for Education (RSPE) u Instructions to be emailed. 23