Mazes In Theory of Computer Science Dana Moshkovitz

Mazes In Theory of Computer Science Dana Moshkovitz 1

Can You Solve This Maze? 2

The Solution 3

Introduction • Objectives: – To explore the undirected connectivity problem – To introduce randomized computations • Overview: – Undirected Connectivity – Random Walks 4

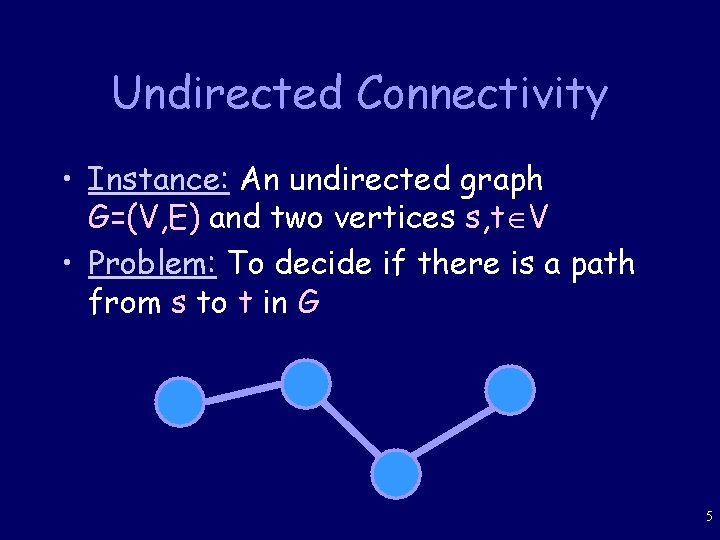
Undirected Connectivity • Instance: An undirected graph G=(V, E) and two vertices s, t V • Problem: To decide if there is a path from s to t in G 5

What Do We Know? Theorem: Directed Connectivity is NL-Complete Corollary: Undirected Connectivity is in NL. 6

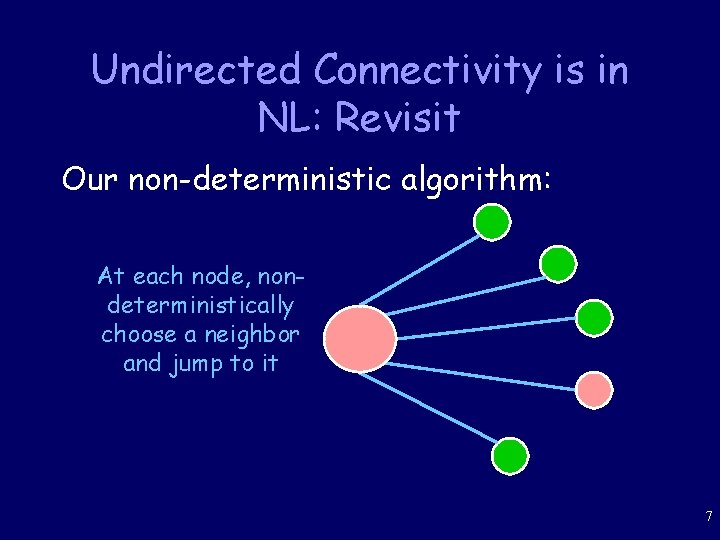
Undirected Connectivity is in NL: Revisit Our non-deterministic algorithm: At each node, nondeterministically choose a neighbor and jump to it 7

What If We Don’t Have “Magic Coins”? • Non-deterministic “algorithms” use “magic coins” to lead them to the right solution if one exists. • In real life, these are unavailable… 8

Idea! • What if we have plain coins? • In other words, what if we randomly choose a neighbor? 9

Random Walks Add a self loop to each vertex. • Start at s. • Let di be the degree of the current node. • Jump to each of the neighbors with probability 1/di. • Stop if you get to t. s t 10

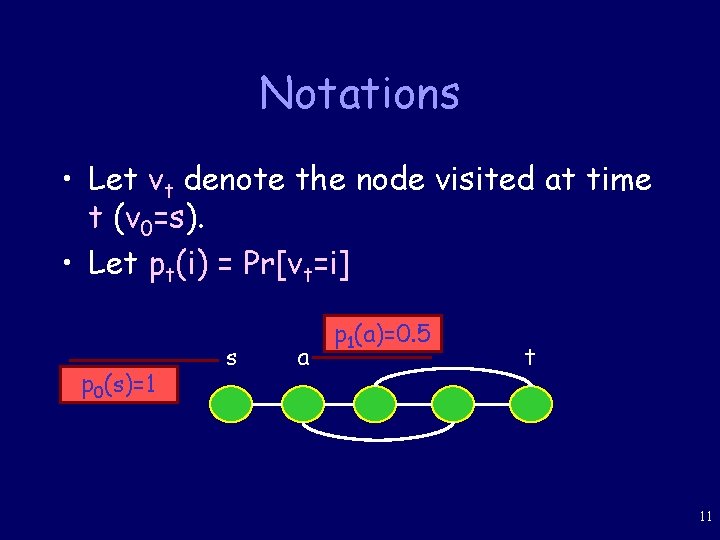
Notations • Let vt denote the node visited at time t (v 0=s). • Let pt(i) = Pr[vt=i] p 0(s)=1 s a p 1(a)=0. 5 t 11

Stationary Distribution Lemma: If G=(V, E) is a connected graph, for any i V, 12

Weaker Claim We’ll prove a weaker result: Lemma: If for some t, for any i V, then for any i V, 13

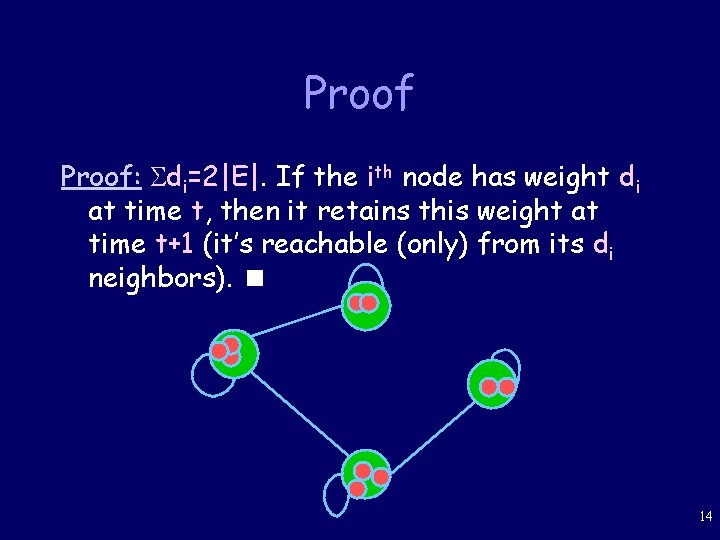
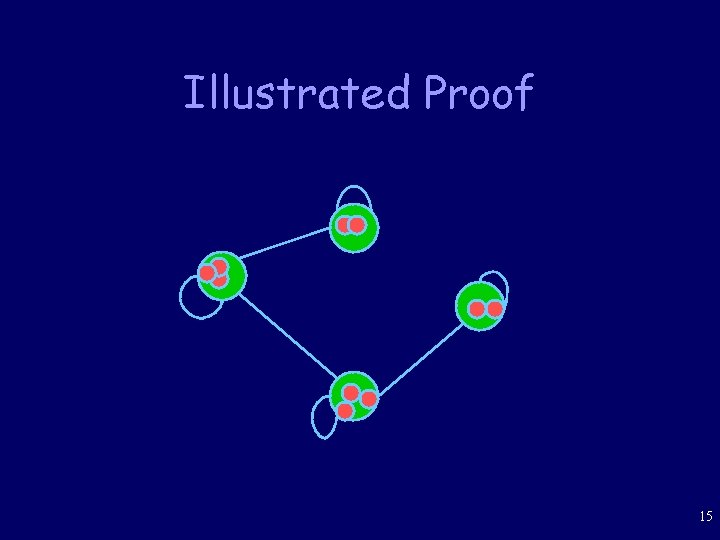
Proof: di=2|E|. If the ith node has weight di at time t, then it retains this weight at time t+1 (it’s reachable (only) from its di neighbors). 14

Illustrated Proof 15

Using the Asymptotic Estimate Corollary: Starting from some node i, we will revisit i within expectedly 2|E|/di steps. 16

One-Sided Error • Note that if the right answer is ‘NO’, we clearly answer ‘NO’. • Thus, a random walk algorithm has onesided error. • Such algorithms are called “Monte-Carlo” algorithms. 17

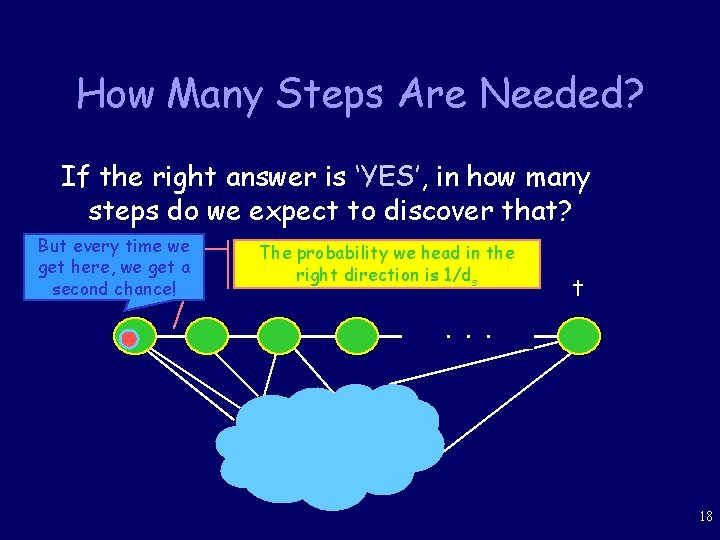
How Many Steps Are Needed? If the right answer is ‘YES’, in how many steps do we expect to discover that? But every time we get here, we get a second chance! s The probability we head in the right direction is 1/ds t . . . 18

How Many Steps Are Needed? • Since expectedly we return to each vertex after 2|E|/di steps, • We expect to head in the right direction after |E| steps (w. p. ½). • By the linearity of the expectation, we expect to encounter t in d(s, t) |E| |V| |E| steps. 19

Randomized Algorithm for Undirected Connectivity 1. Run the random walk from s for 2|V| |E| steps. 2. If node t is ever visited, answer “there is a path from s to t”. 3. Otherwise, reply “there is probably no path from s to t”. 20

PAP 401 -404 Main Theorem: The above algorithm To maintain the current position we only need - uses logarithmic space log|V| space - always right for ‘NO’ instances. - errs with probability at most ½ for ‘YES’ instances. Markov: Pr(X>2 E[X])<½ 21

Summary • We explored the undirected connectivity problem. • We saw a log-space randomized algorithm for this problem. • We used an important technique called random walks. 22