Mazes And Random Walks Complexity 1 Can You
















- Slides: 23

Mazes And Random Walks Complexity 1

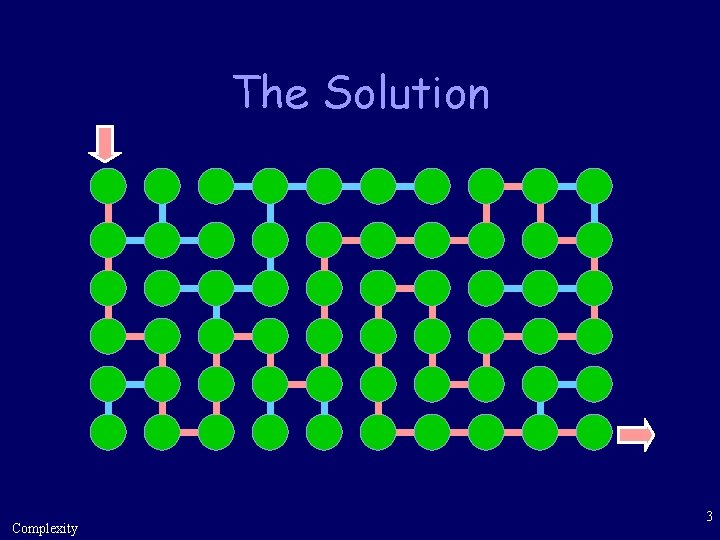
Can You Solve This Maze? Complexity 2

The Solution Complexity 3

What Will We Do? • Our task is to show an algorithm for general mazes. • We have memory which is logarithmic in the size of the maze. Complexity 4

Introduction • Objectives: – To explore the undirected connectivity problem – To introduce randomized computations • Overview: – Undirected Connectivity – Random Walks Complexity 5

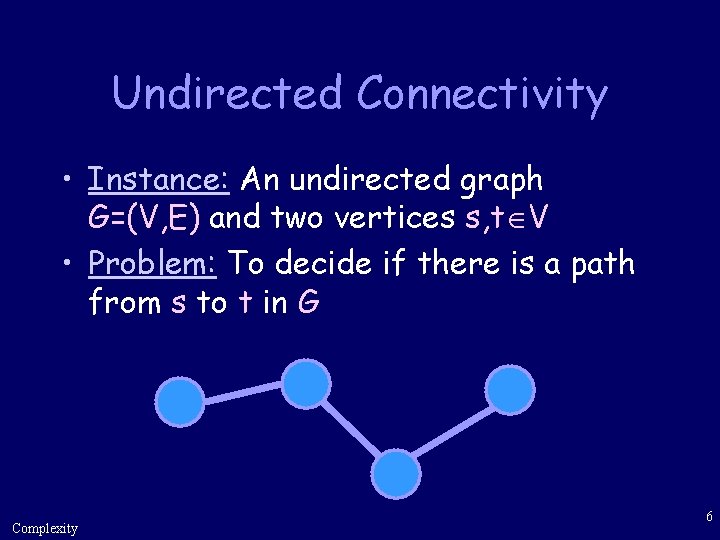
Undirected Connectivity • Instance: An undirected graph G=(V, E) and two vertices s, t V • Problem: To decide if there is a path from s to t in G Complexity 6

What Do We Know? Theorem: Directed Connectivity is NL-Complete Corollary: Undirected Connectivity is in NL. Complexity 7

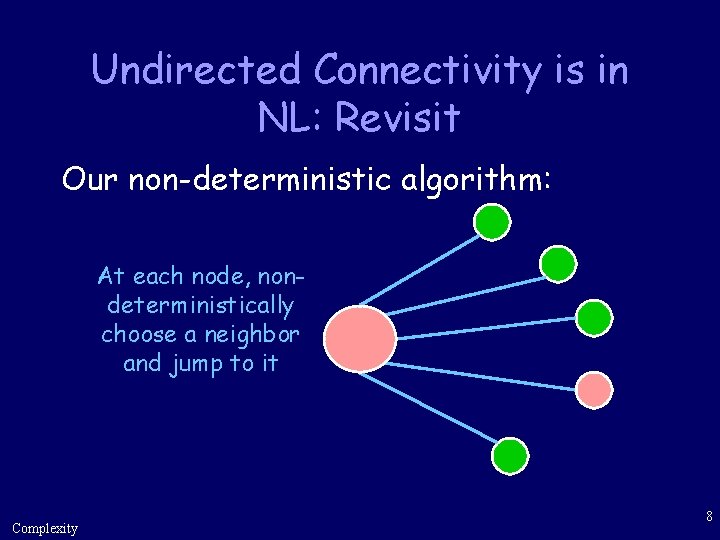
Undirected Connectivity is in NL: Revisit Our non-deterministic algorithm: At each node, nondeterministically choose a neighbor and jump to it Complexity 8

What If We Don’t Have “Magic Coins”? • Non-deterministic “algorithms” use “magic coins” to lead them to the right solution if one exists. • In real life, these are unavailable… Complexity 9

Idea! • What if we have plain coins? • In other words, what if we randomly choose a neighbor? Complexity 10

Random Walks Add a self loop to each vertex. • Start at s. • Let di be the degree of the current node. • Jump to each of the neighbors with probability 1/di. • Stop if you get to t. s Complexity t 11

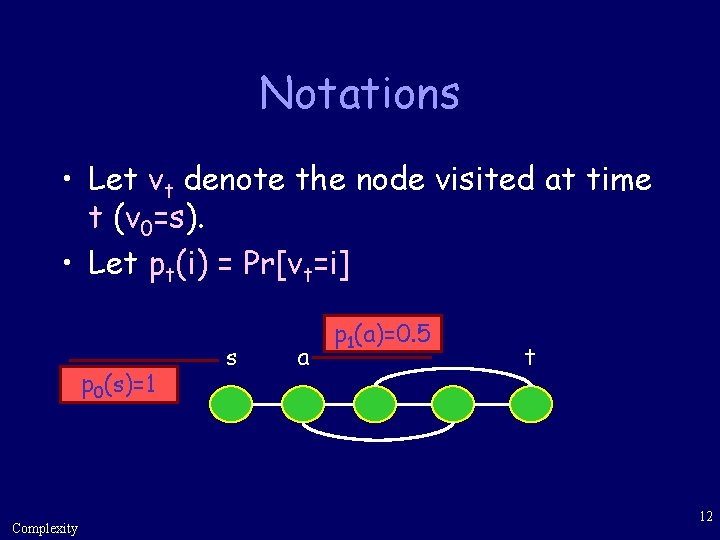
Notations • Let vt denote the node visited at time t (v 0=s). • Let pt(i) = Pr[vt=i] p 0(s)=1 Complexity s a p 1(a)=0. 5 t 12

Stationary Distribution Lemma: If G=(V, E) is a connected graph, for any i V, Complexity 13

Weaker Claim We’ll prove a weaker result: Lemma: If for some t, for any i V, then for any i V, Complexity 14

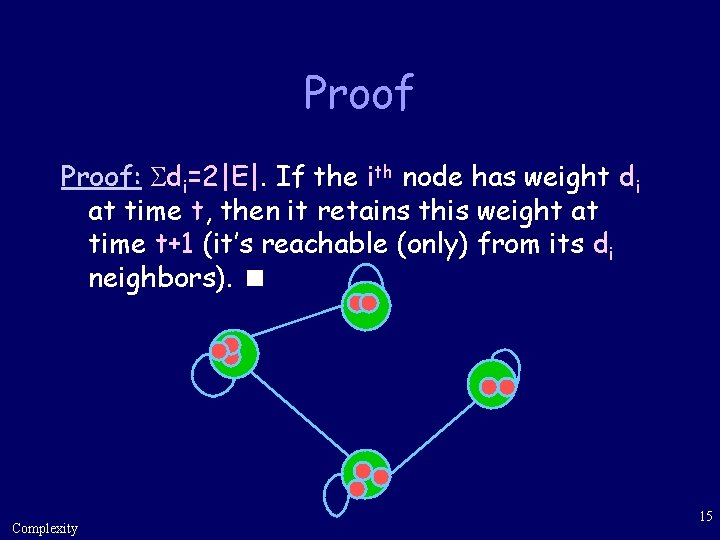
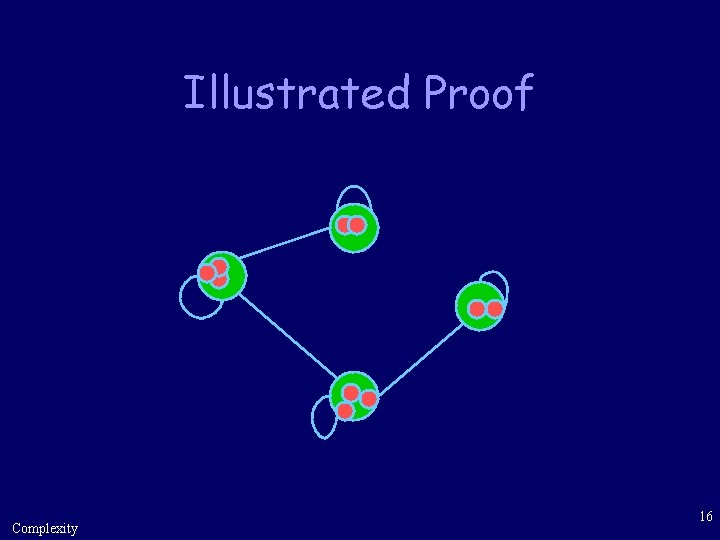
Proof: di=2|E|. If the ith node has weight di at time t, then it retains this weight at time t+1 (it’s reachable (only) from its di neighbors). Complexity 15

Illustrated Proof Complexity 16

Using the Asymptotic Estimate Corollary: Starting from some node i, we will revisit i within expectedly 2|E|/di steps. Proof: Since the walk has no “memory”, the expected return time is the same as the asymptotic estimate Complexity 17

One-Sided Error • Note that if the right answer is ‘NO’, we clearly answer ‘NO’. • Thus, a random walk algorithm has onesided error. • Such algorithms are called “Monte-Carlo” algorithms. Complexity 18

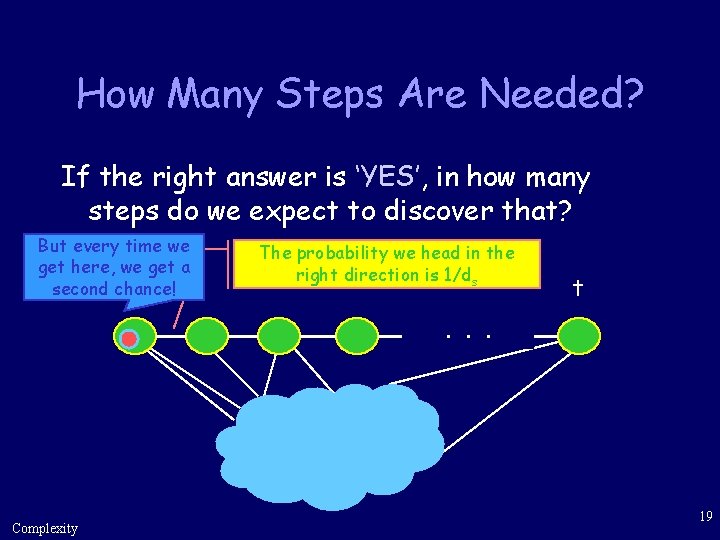
How Many Steps Are Needed? If the right answer is ‘YES’, in how many steps do we expect to discover that? But every time we get here, we get a second chance! s The probability we head in the right direction is 1/ds t . . . Complexity 19

How Many Steps Are Needed? • Since expectedly we return to each vertex after 2|E|/di steps, • We expect to head in the right direction after |E| steps (w. p. ½). • By the linearity of the expectation, we expect to encounter t in d(s, t) |E| |V| |E| steps. Complexity 20

Randomized Algorithm for Undirected Connectivity 1. Run the random walk from s for 2|V| |E| steps. 2. If node t is ever visited, answer “there is a path from s to t”. 3. Otherwise, reply “there is probably no path from s to t”. Complexity 21

PAP 401 -404 Main Theorem: The above algorithm To maintain the current position we only need - uses logarithmic space log|V| space - always right for ‘NO’ instances. - errs with probability at most ½ for ‘YES’ instances. Markov: Pr(X>2 E[X])<½ Complexity 22

Summary • We explored the undirected connectivity problem. • We saw a log-space randomized algorithm for this problem. • We used an important technique called random walks. Complexity 23