Maze Routing Steiner Trees With Delay vs Wire



















- Slides: 59

Maze Routing Steiner Trees With Delay vs. Wire Length Trade-off Renato Hentschke Jaganathan Narasimham Marcelo Johann Ricardo Reis Universidade Federal do Rio Grande do Sul {renato, johann, reis}@inf. ufrgs. br ISPD 2007 IBM - Thomas Watson RC jagan@us. ibm. com

Where are the rest of us from? Porto Alegre RS - Brasil

This work presents… AMAZE Let us start with a little… FAQ Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

What is AMAZE? An algorithm for • single net Steiner Tree construction • that uses A* searches • and trades-off WL for delay Actual Routing Can do both Tree Topologies Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

In which context AMAZE fits in? Steiner Trees are used for estimation and perhaps global routing Maze Router is widely used for actual routing (global or detailed) Somewhere in the flow we decompose the nets by setting Steiner points or just forget our Steiner Trees and let the router run… Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

What is the motivation? Maze Router has a lot of potential: Net ordering can be aliviated by negotiation Speed can be improved (a lot) with A* searches and by tuning data structures Memory is not a concern for most applications Degrees of freedom can be exploited to get quality results, e. g. , good Trees Keep Maze router’s nice properties Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

How good can AMAZE be? What about: Within 2% from optimal Steiner Trees? From 26% to 40% improvement in delay compared to AHHK? From 1% to 30% improvement in delay compared to P-Trees? As fast as any heuristic Steiner Tree algorithm Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

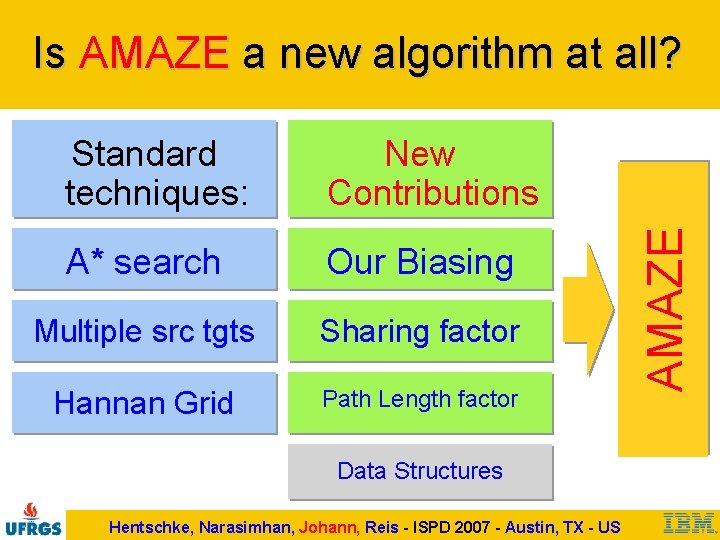
Standard techniques: New Contributions A* search Our Biasing Multiple src tgts Sharing factor Hannan Grid Path Length factor Data Structures Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US AMAZE Is AMAZE a new algorithm at all?

What not to expect from AMAZE? The main weaknesses are (currently): Cannot guarantee efficiency (speed) or quality (good trees) with costs that vary too much. Problem for global routing that has to model congestion We have not checked if early estimation matches actual routing if context changes Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Outline 1. 2. 3. 4. 5. 6. 7. Delay and WL trade-off Properties of A* Creating Steiner Trees with A* Improving Wirelenght Improving Delay to critical sinks Experimental results Concluding remarks Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

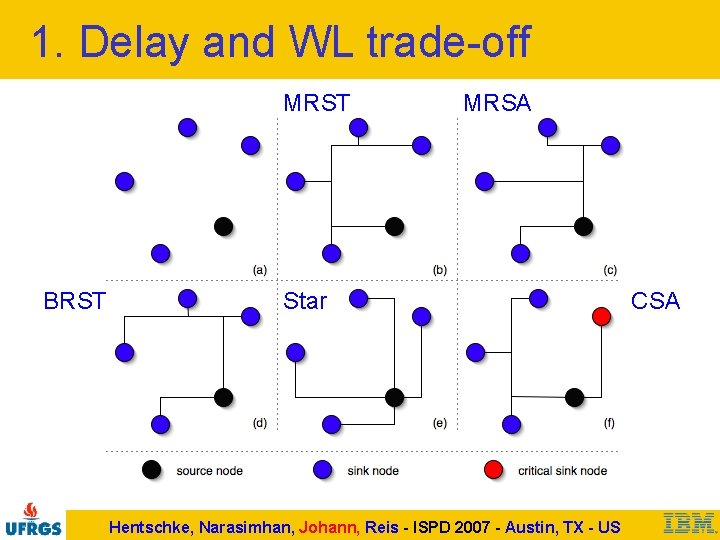
1. Delay and WL trade-off MRST BRST MRSA Star Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US CSA

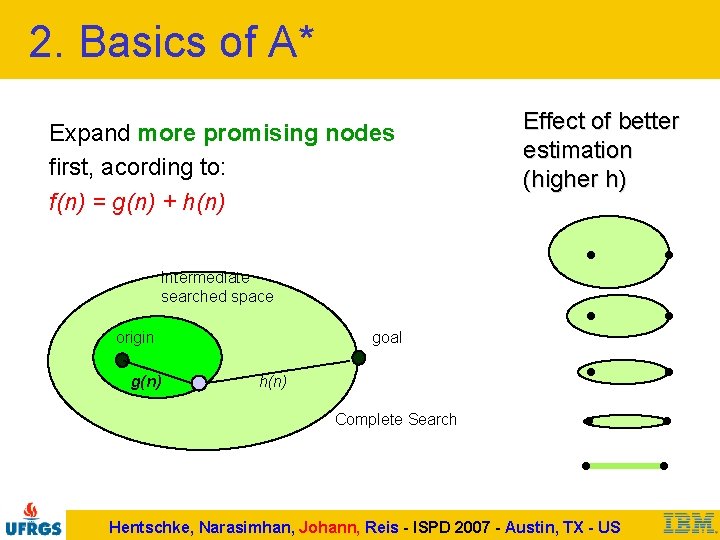
2. Basics of A* Expand more promising nodes first, acording to: f(n) = g(n) + h(n) Effect of better estimation (higher h) Intermediate searched space origin g(n) goal h(n) Complete Search Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

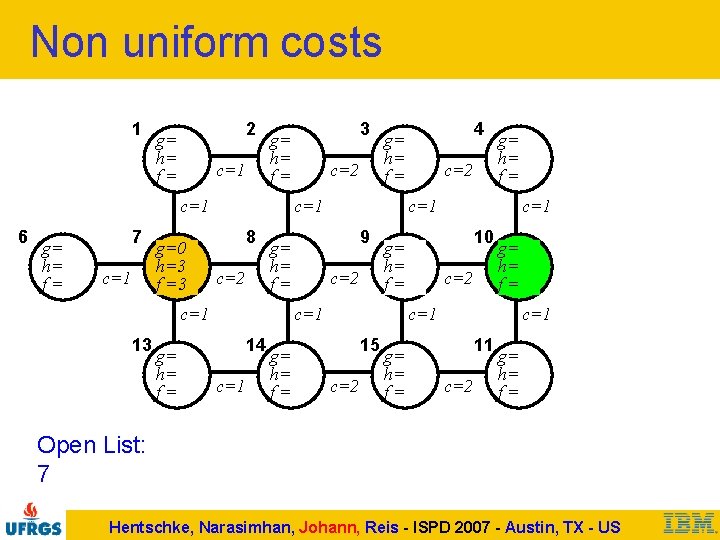
Non uniform costs 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=0 h=3 f =3 g= h= f= c=2 8 c=2 c=1 g= h= f= c=1 10 g= h= f= c=1 14 c=2 g= h= f= c=1 9 g= h= f= 4 g= h= f= c=1 13 3 g= h= f= c=2 g= h= f= c=1 15 c=2 g= h= f= c=1 11 c=2 g= h= f= Open List: 7 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

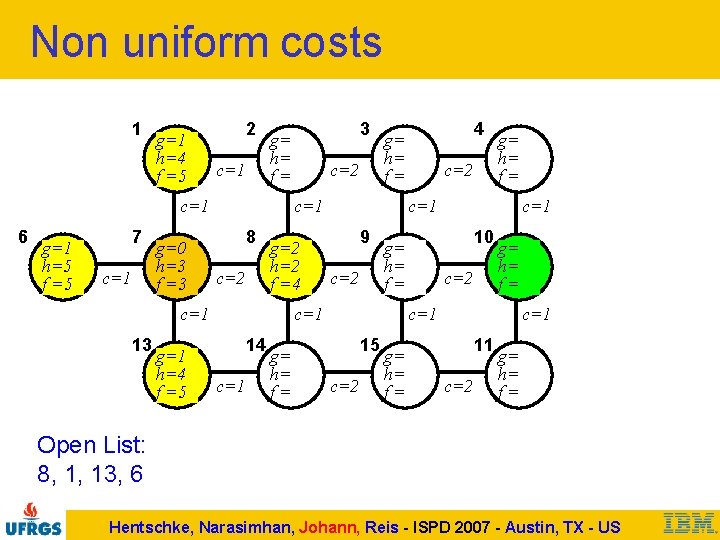
Non uniform costs 1 g=1 h=4 f =5 2 c=1 6 g=1 h=5 f =5 7 c=1 g=0 h=3 f =3 g=1 h=4 f =5 c=2 8 c=2 g=2 h=2 f =4 c=1 g= h= f= c=2 g= h= f= c=1 9 c=2 c=1 10 g= h= f= c=1 14 4 g= h= f= c=1 13 3 g= h= f= c=2 g= h= f= c=1 15 c=2 g= h= f= c=1 11 c=2 g= h= f= Open List: 8, 1, 13, 6 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

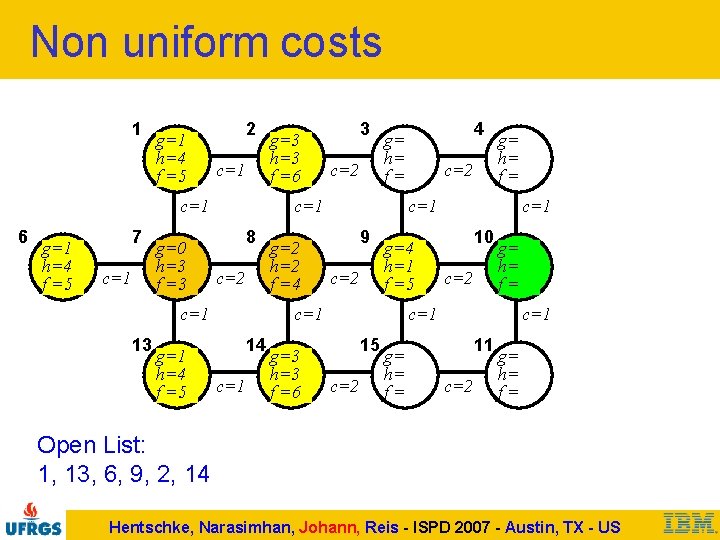
Non uniform costs 1 g=1 h=4 f =5 2 c=1 6 g=1 h=4 f =5 7 c=1 g=0 h=3 f =3 g=1 h=4 f =5 3 c=2 8 c=2 g=2 h=2 f =4 c=1 g=3 h=3 f =6 c=2 g= h= f= c=1 9 c=2 g=4 h=1 f =5 c=1 14 4 g= h= f= c=1 13 g=3 h=3 f =6 c=1 10 c=2 g= h= f= c=1 15 c=2 g= h= f= c=1 11 c=2 g= h= f= Open List: 1, 13, 6, 9, 2, 14 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

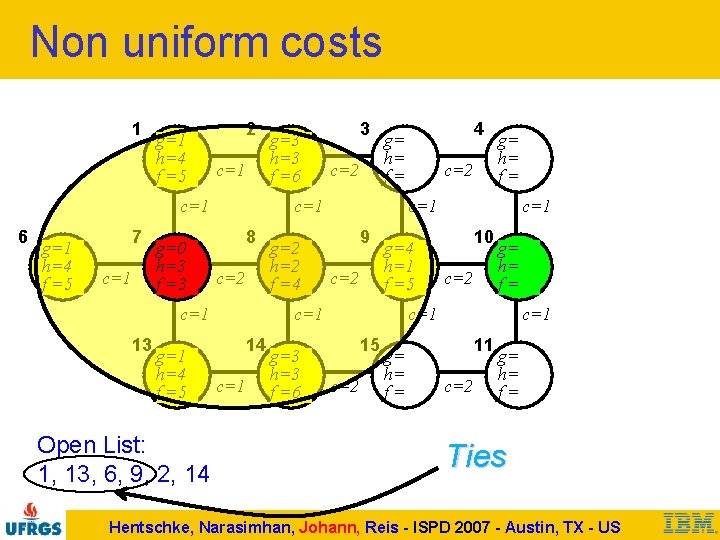
Non uniform costs 1 g=1 h=4 f =5 2 c=1 6 g=1 h=4 f =5 7 c=1 g=0 h=3 f =3 g=1 h=4 f =5 Open List: 1, 13, 6, 9, 2, 14 3 c=2 8 c=2 g=2 h=2 f =4 c=1 g=3 h=3 f =6 c=2 g= h= f= c=1 9 c=2 g=4 h=1 f =5 c=1 14 4 g= h= f= c=1 13 g=3 h=3 f =6 c=1 10 c=2 g= h= f= c=1 15 c=2 g= h= f= c=1 11 c=2 g= h= f= Ties Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

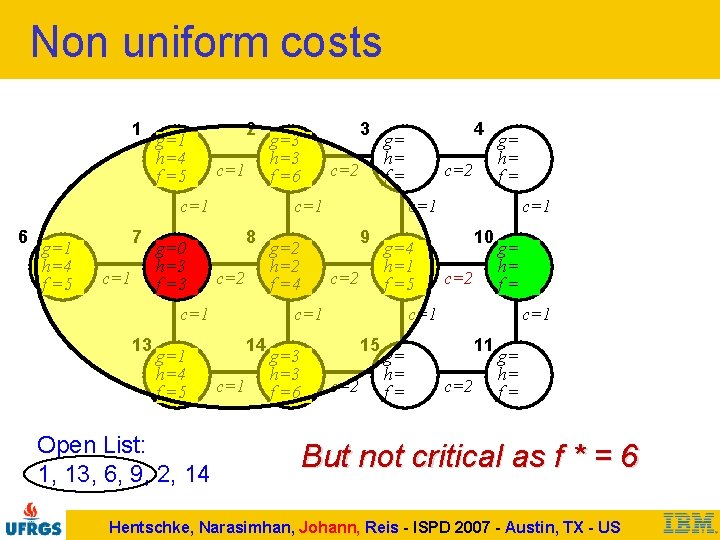
Non uniform costs 1 g=1 h=4 f =5 2 c=1 6 g=1 h=4 f =5 7 c=1 g=0 h=3 f =3 g=1 h=4 f =5 Open List: 1, 13, 6, 9, 2, 14 c=2 8 c=2 g=4 h=1 f =5 c=1 14 c=1 g=3 h=3 f =6 c=2 g= h= f= c=1 9 g=2 h=2 f =4 4 g= h= f= c=1 13 3 g=3 h=3 f =6 c=1 10 c=2 g= h= f= c=1 15 c=2 g= h= f= c=1 11 c=2 g= h= f= But not critical as f * = 6 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

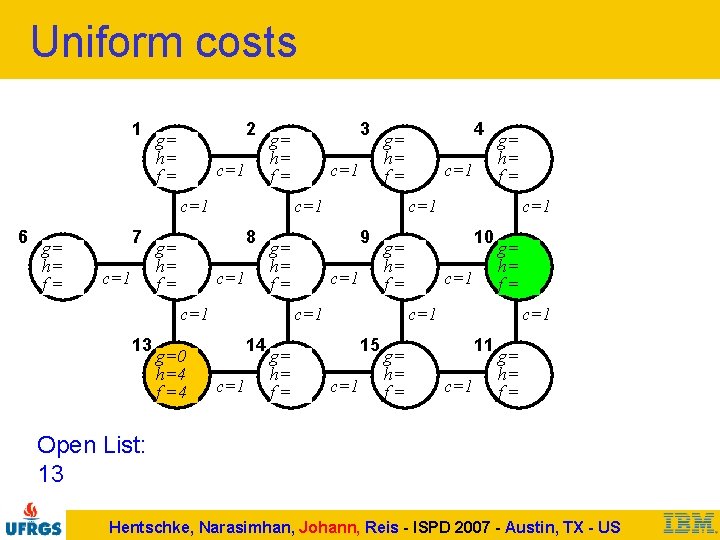
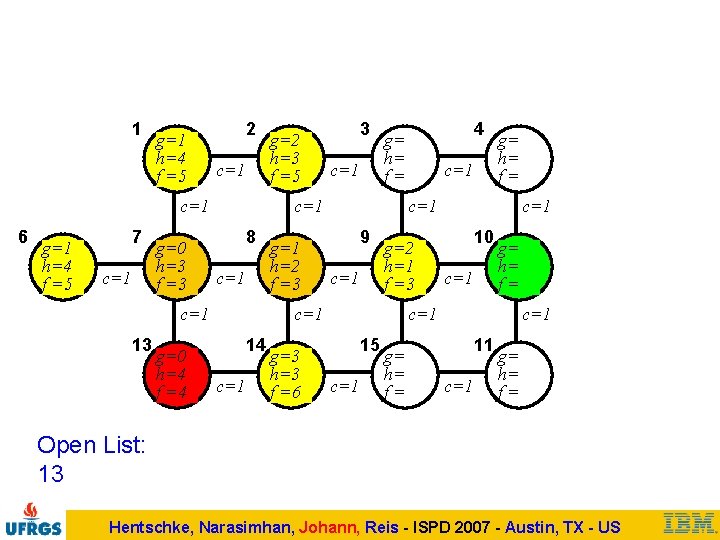
Uniform costs 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=0 h=4 f =4 c=1 g= h= f= c=1 10 g= h= f= c=1 14 c=1 g= h= f= c=1 9 g= h= f= c=1 13 c=1 4 g= h= f= c=1 8 g= h= f= 3 g= h= f= c=1 15 c=1 g= h= f= c=1 11 c=1 g= h= f= Open List: 13 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

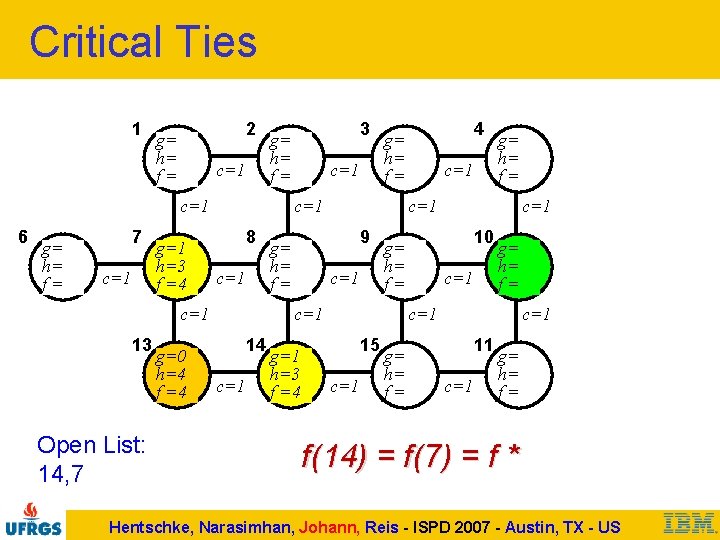
Critical Ties 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 14, 7 g=0 h=4 f =4 c=1 8 c=1 c=1 g=1 h=3 f =4 c=1 10 g= h= f= c=1 14 c=1 g= h= f= c=1 9 g= h= f= 4 g= h= f= c=1 13 3 g= h= f= c=1 15 c=1 g= h= f= c=1 11 c=1 g= h= f= f(14) = f(7) = f * Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

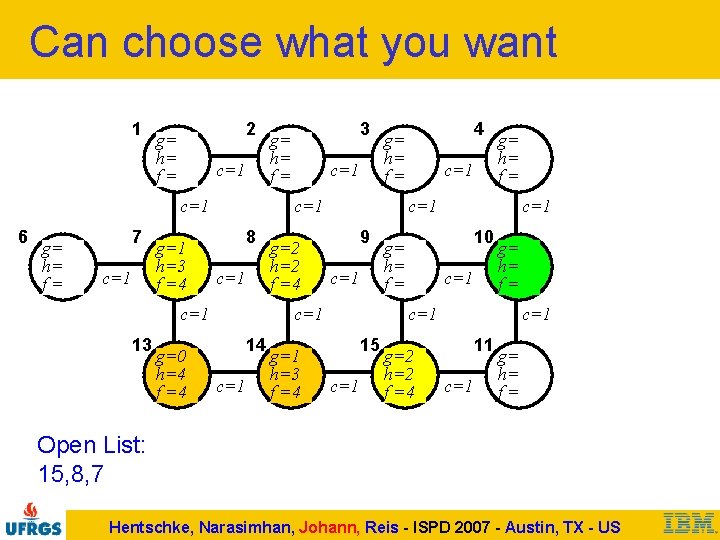
Can choose what you want 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 g=0 h=4 f =4 c=1 8 c=1 g=2 h=2 f =4 c=1 g=1 h=3 f =4 c=1 g= h= f= c=1 9 c=1 14 4 g= h= f= c=1 13 3 g= h= f= c=1 10 g= h= f= c=1 15 c=1 g=2 h=2 f =4 c=1 11 c=1 g= h= f= Open List: 15, 8, 7 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

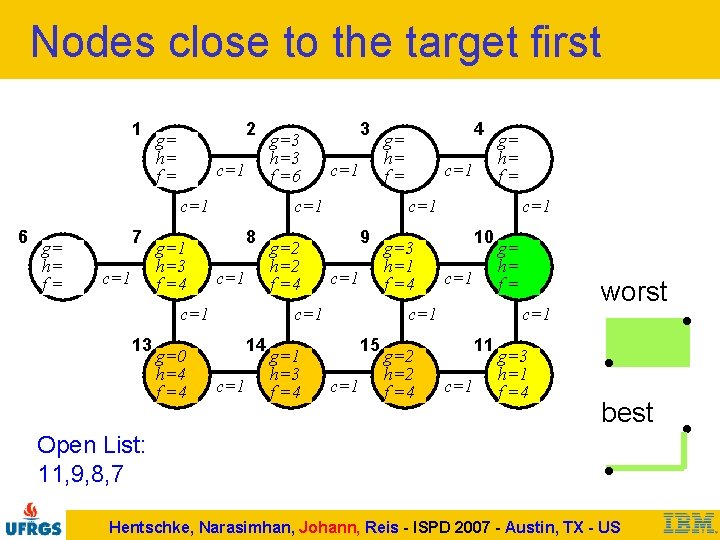
Nodes close to the target first 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 g=0 h=4 f =4 3 c=1 8 c=1 13 g=3 h=3 f =6 g=2 h=2 f =4 c=1 g=1 h=3 f =4 c=1 g= h= f= c=1 9 c=1 14 4 g= h= f= g=3 h=1 f =4 c=1 10 c=1 15 c=1 g=2 h=2 f =4 g= h= f= c=1 11 c=1 g=3 h=1 f =4 worst best Open List: 11, 9, 8, 7 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

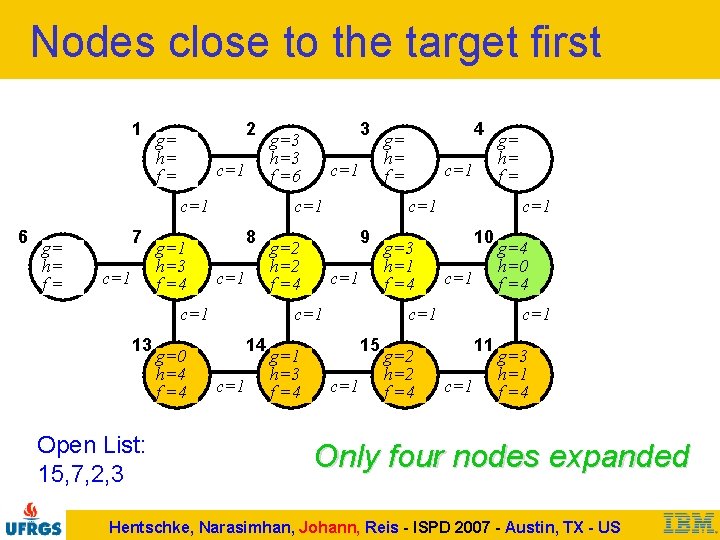
Nodes close to the target first 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 15, 7, 2, 3 g=0 h=4 f =4 c=1 8 c=1 13 3 g=3 h=3 f =6 c=1 14 c=1 g=1 h=3 f =4 c=1 9 g=2 h=2 f =4 4 g= h= f= g=3 h=1 f =4 c=1 10 c=1 15 c=1 g=2 h=2 f =4 g= h= f= g=4 h=0 f =4 c=1 11 c=1 g=3 h=1 f =4 Only four nodes expanded Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

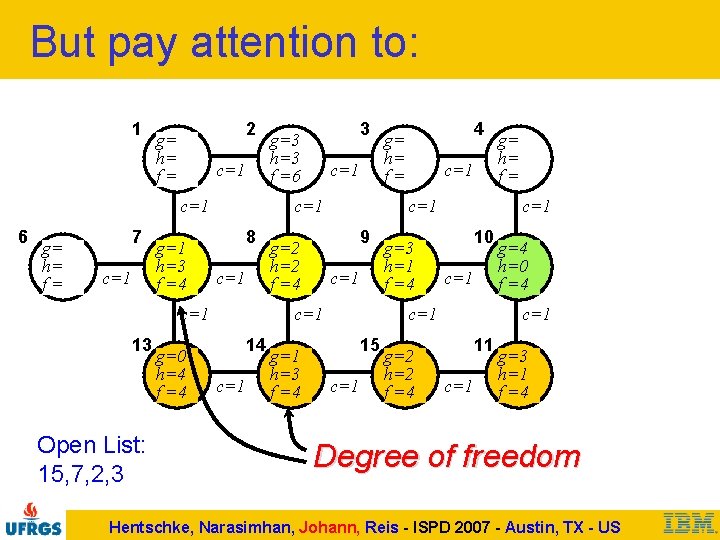
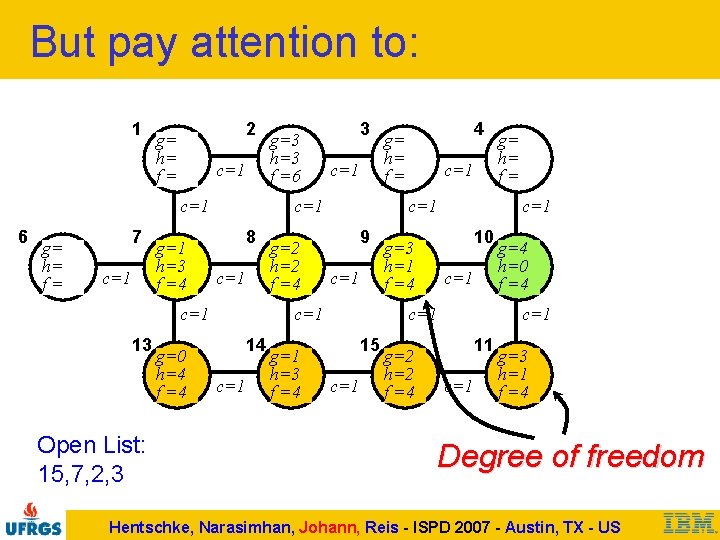
But pay attention to: 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 15, 7, 2, 3 g=0 h=4 f =4 c=1 8 c=1 13 3 g=3 h=3 f =6 c=1 14 c=1 g=1 h=3 f =4 c=1 9 g=2 h=2 f =4 4 g= h= f= g=3 h=1 f =4 c=1 10 c=1 15 c=1 g=2 h=2 f =4 g= h= f= g=4 h=0 f =4 c=1 11 c=1 g=3 h=1 f =4 Degree of freedom Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

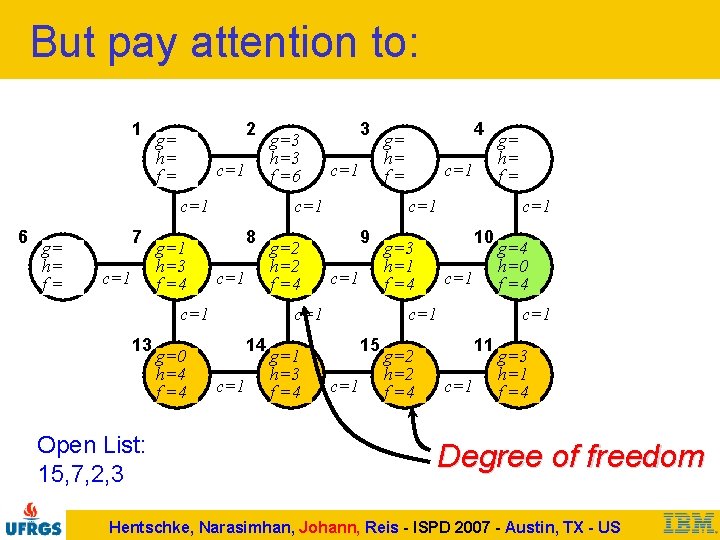
But pay attention to: 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 15, 7, 2, 3 g=0 h=4 f =4 3 c=1 8 c=1 13 g=3 h=3 f =6 g=2 h=2 f =4 c=1 g=1 h=3 f =4 c=1 9 c=1 14 4 g= h= f= c=1 10 g=3 h=1 f =4 c=1 15 c=1 g=2 h=2 f =4 g= h= f= g=4 h=0 f =4 c=1 11 c=1 g=3 h=1 f =4 Degree of freedom Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

But pay attention to: 1 2 g= h= f= c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 15, 7, 2, 3 g=0 h=4 f =4 3 c=1 8 c=1 13 g=3 h=3 f =6 g=2 h=2 f =4 c=1 g=1 h=3 f =4 c=1 9 c=1 14 4 g= h= f= c=1 10 g=3 h=1 f =4 c=1 15 c=1 g=2 h=2 f =4 g= h= f= g=4 h=0 f =4 c=1 11 c=1 g=3 h=1 f =4 Degree of freedom Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

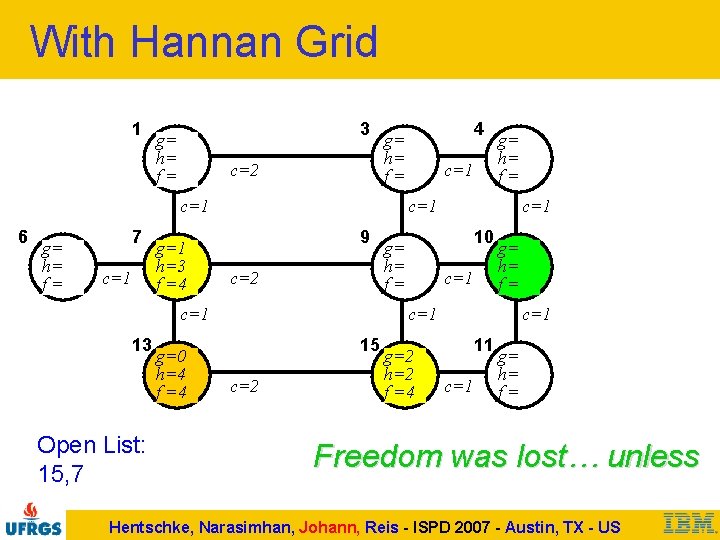
With Hannan Grid 1 3 g= h= f= c=2 c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 15, 7 g=0 h=4 f =4 c=1 g= h= f= c=1 9 c=2 c=1 13 4 g= h= f= c=1 10 g= h= f= c=1 15 c=2 g=2 h=2 f =4 c=1 11 c=1 g= h= f= Freedom was lost… unless Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

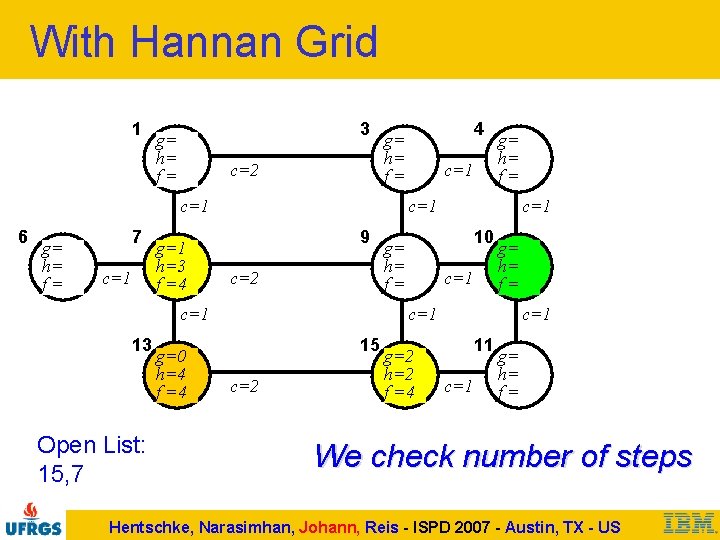
With Hannan Grid 1 3 g= h= f= c=2 c=1 6 g= h= f= 7 c=1 g=1 h=3 f =4 Open List: 15, 7 g=0 h=4 f =4 c=1 g= h= f= c=1 9 c=2 c=1 13 4 g= h= f= c=1 10 g= h= f= c=1 15 c=2 g=2 h=2 f =4 c=1 11 c=1 g= h= f= We check number of steps Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Summary Simple ties f = f all expanded Critical ties f=f=f* break for efficiency Depth ties f=f=f* and g=g true freedom Stepped depth ties f=f=f* and s=s w/Hannan Net result: Best efficiency, freedom to chose the paths Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

3. Creating Steiner Trees with A* Sinks are added one by one Multiple Sources connected tree Which target to connect next? Multiple Targets select the best accounts for blockages h function sees all sinks chosen target ct(n) used for speed First route all critical sinks (later on) Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

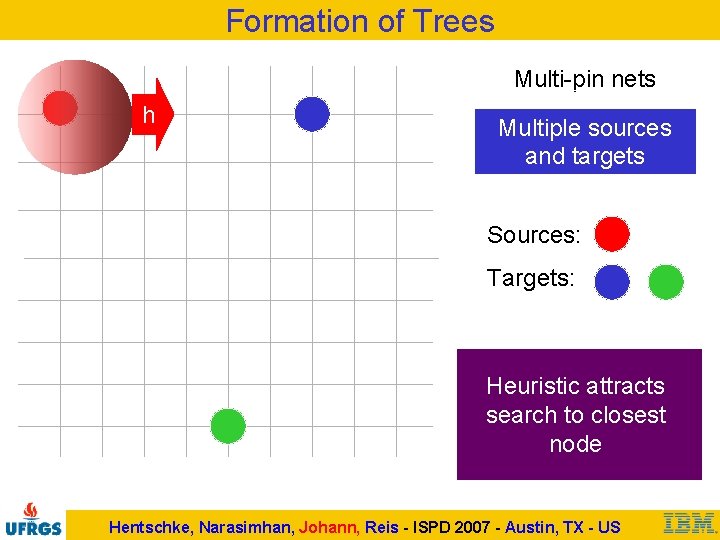
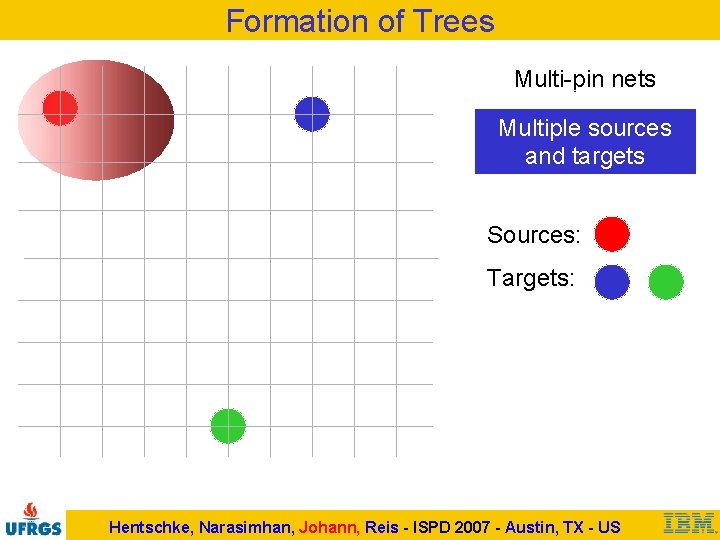
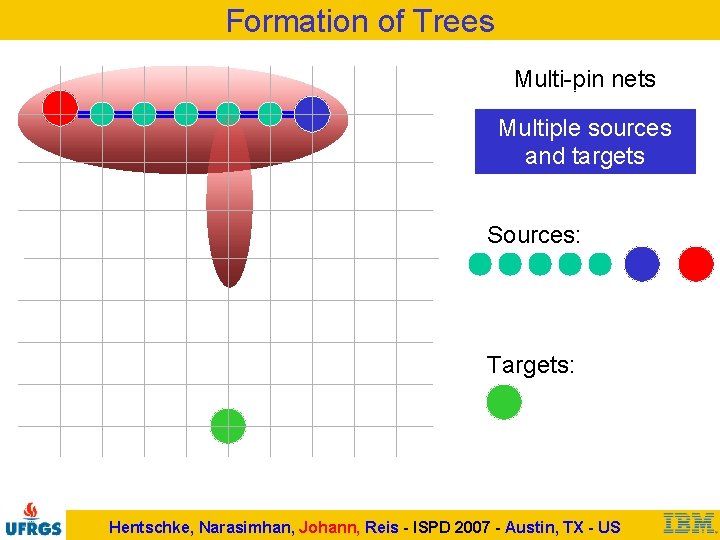
Formation of Trees Multi-pin nets h Multiple sources and targets Sources: Targets: Heuristic attracts search to closest node Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Formation of Trees Multi-pin nets Multiple sources and targets Sources: Targets: Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

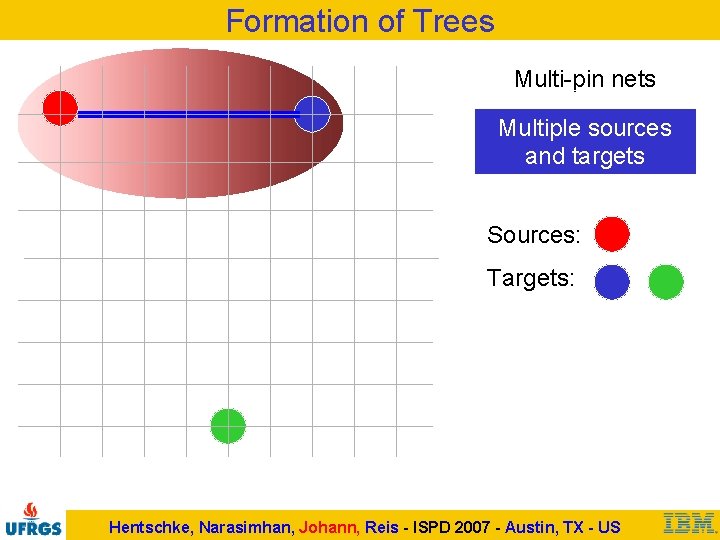
Formation of Trees Multi-pin nets Multiple sources and targets Sources: Targets: Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Formation of Trees Multi-pin nets Multiple sources and targets Sources: Targets: Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

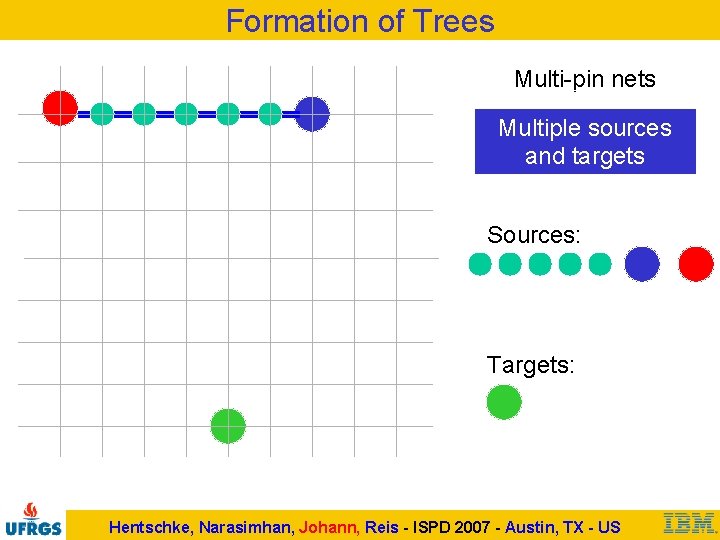
Formation of Trees Multi-pin nets Multiple sources and targets Sources: Targets: Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Formation of Trees Multi-pin nets Multiple sources and targets Sources: Targets: Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

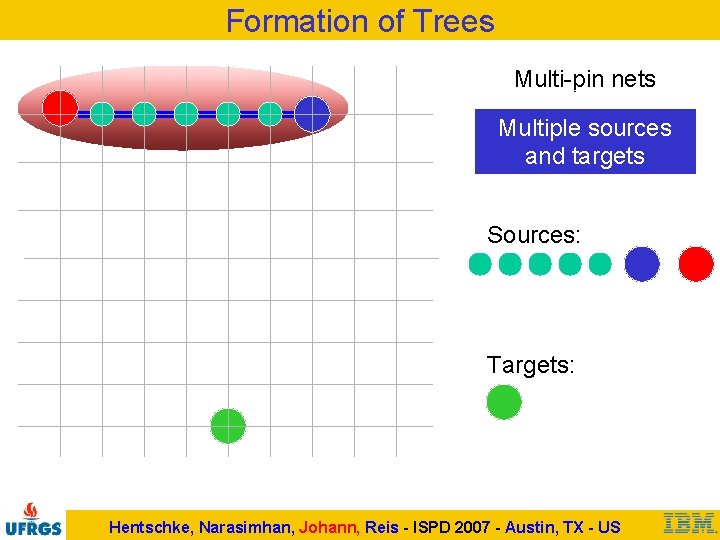
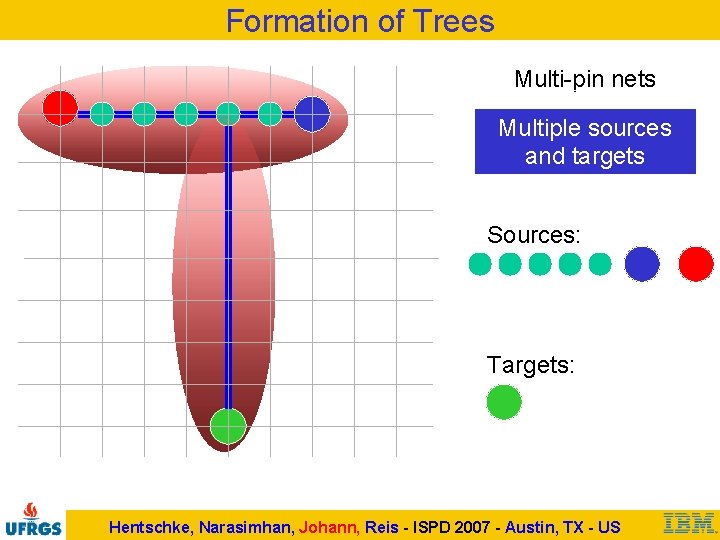
Formation of Trees Multi-pin nets Multiple sources and targets Sources: Targets: Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

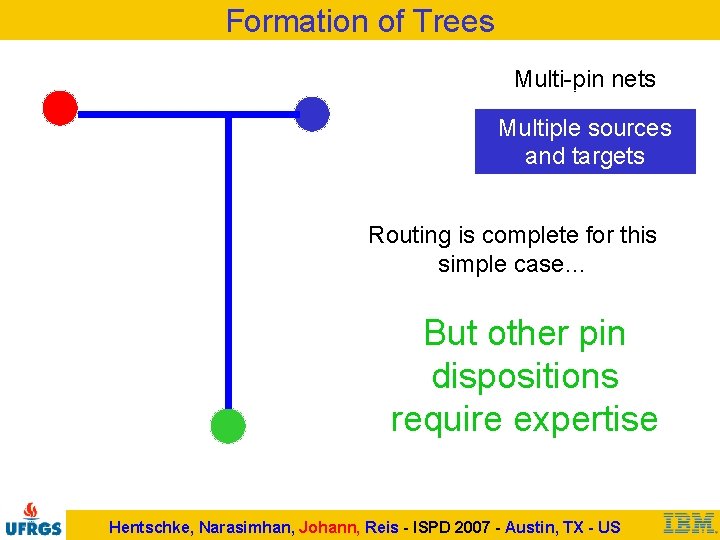
Formation of Trees Multi-pin nets Multiple sources and targets Routing is complete for this simple case… But other pin dispositions require expertise Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Select targets with A* Sinks are added one by one Multiple Sources connected tree Which target to connect next? Multiple Targets select the best accounts for blockages h function sees all sinks chosen target ct(n) used for speed First route all critical sinks (later on) Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

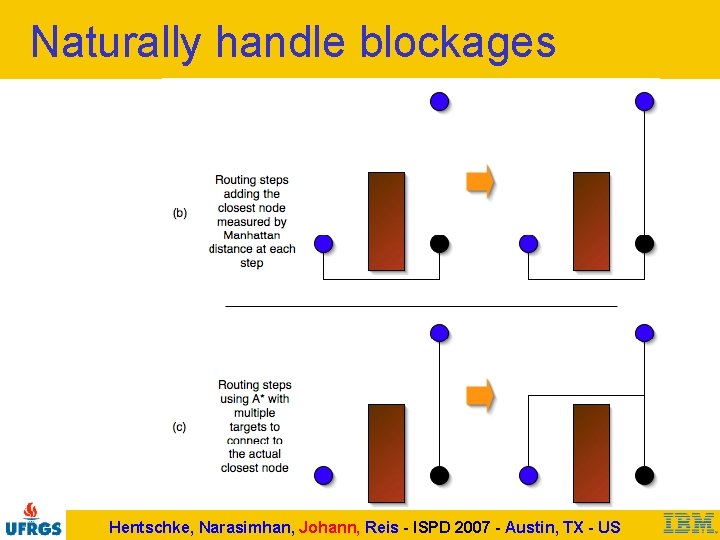
Naturally handle blockages Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

4. Improving Wirelenght Share as many segments as possible Use decision points (freedom) to chose paths closer to other pins Performed by the biasing funcion called when stepped depth ties happen Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

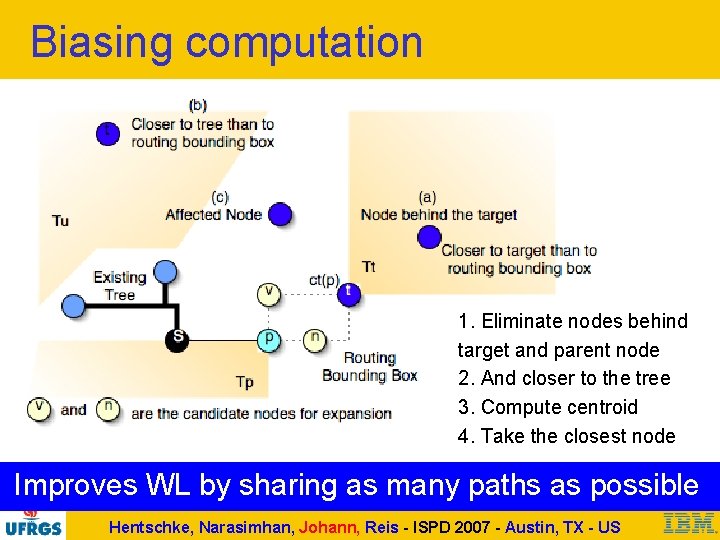
Biasing computation 1. Eliminate nodes behind target and parent node 2. And closer to the tree 3. Compute centroid 4. Take the closest node Improves WL by sharing as many paths as possible Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

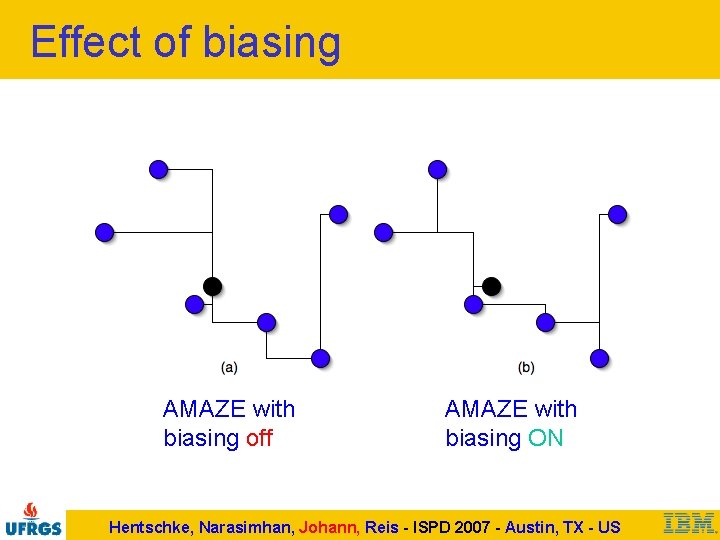
Effect of biasing AMAZE with biasing off AMAZE with biasing ON Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

5. Improving Delay to critical sinks Use as little sharing as possible Route them first Use repulsive biasing Sharing Factor Path Length Factor Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

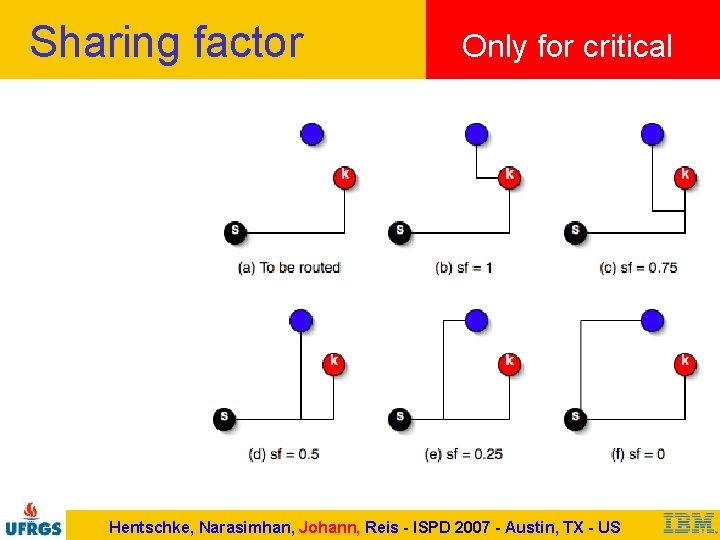
Sharing factor Only for critical Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

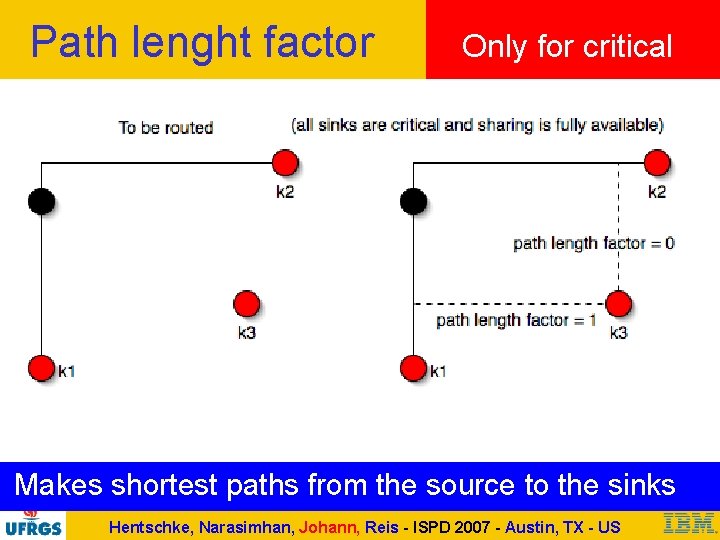
Path lenght factor Only for critical Makes shortest paths from the source to the sinks Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

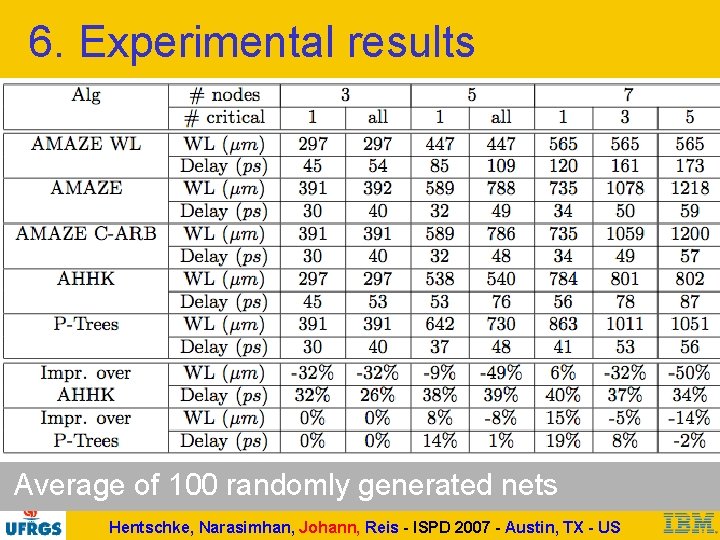
6. Experimental results Average of 100 randomly generated nets Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

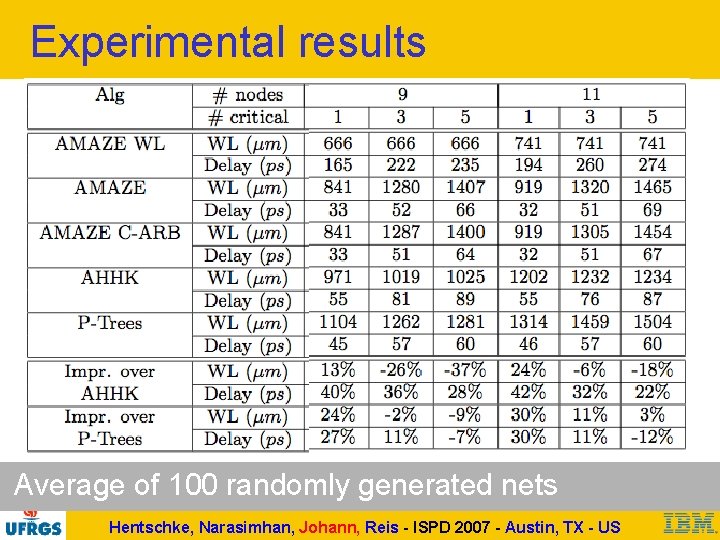
Experimental results Average of 100 randomly generated nets Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

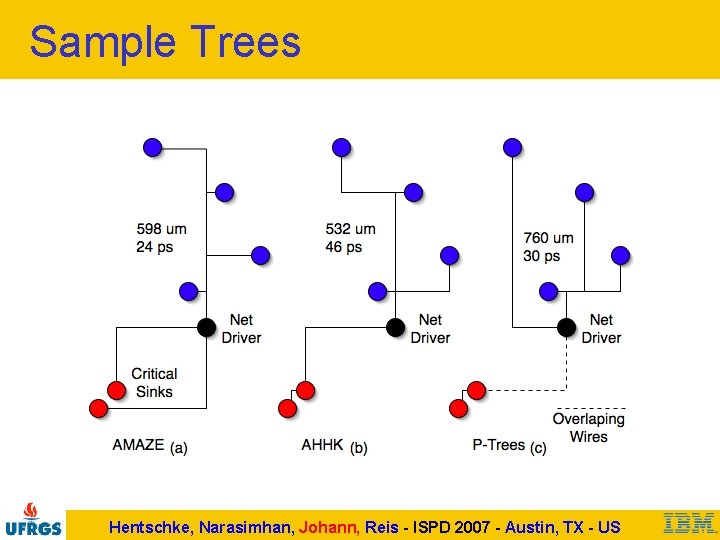
Sample Trees Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

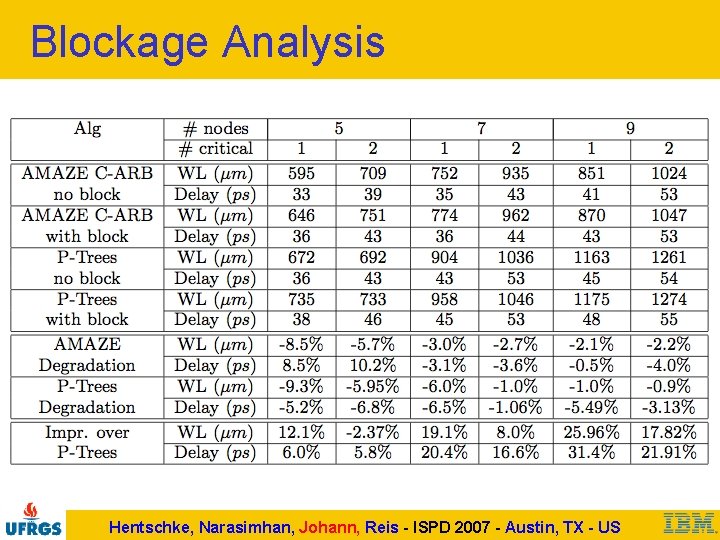
Blockage Analysis Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

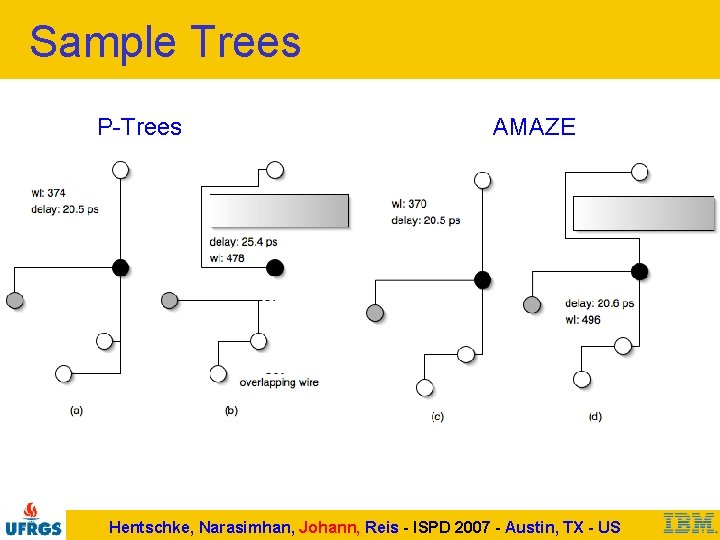
Sample Trees P-Trees AMAZE Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

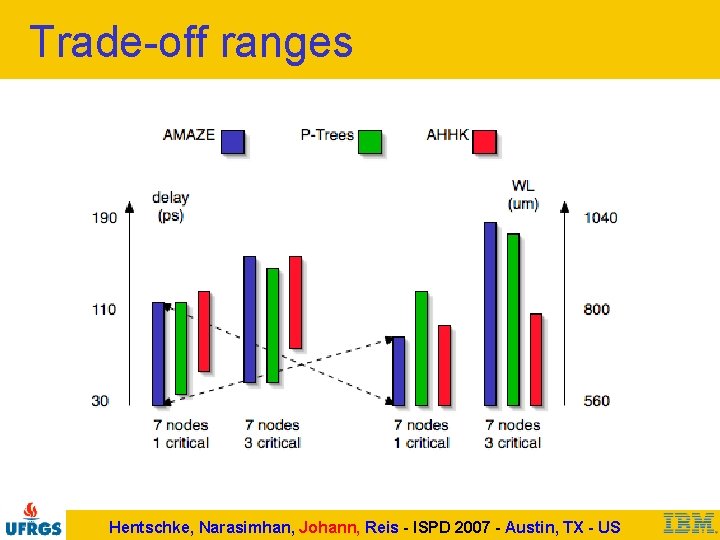
Trade-off ranges Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

7. Concluding remarks Steiner Trees within 2% from optimal Savings of up to 40% in delay / AHHK Savings of up to 30% in delay / P-Trees Wider trade-off ranges for delay and WL Handle blockages better than competitors Flexibility and Speed Application: play with factors and get the best Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Questions? downtown Porto Alegre Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Maze Routing Steiner Trees With Delay vs. Wire Length Trade-off Renato Hentschke Jaganathan Narasimham Marcelo Johann Ricardo Reis Thank you! Universidade Federal do Rio Grande do Sul {renato, johann, reis}@inf. ufrgs. br ISPD 2007 IBM - Thomas Watson RC jagan@us. ibm. com

3. 2 Princípios da Pesquisa A partir de s, formar uma árvore de pesquisa pela aplicação repetitiva do operador de sucessão Um nodo é expandido quando se aplica a operação de sucessão sobre ele (o nodo se torna fechado) Um nodo é gerado quando é retornado pela operação de sucessão (o nodo se torna aberto) v 1 v 3 v 2 v 6 v 8 v 4 v 5 s v 9 v 0 v 7 t admissibility Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Notação s, t - source and target nodes k(n 1, n 2) - estimativa entre n 1 e n 2 k*(n 1, n 2) - custo real entre n 1 e n 2 h(n) = k(n, t) h*(n) = k*(n, t) g*(n) = k*(s, n) Pa-b = caminho de a até b Pa-b* = caminho ótimo de a até b f*(n) = custo de Ps-n* Pn-t* (passando por n) Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

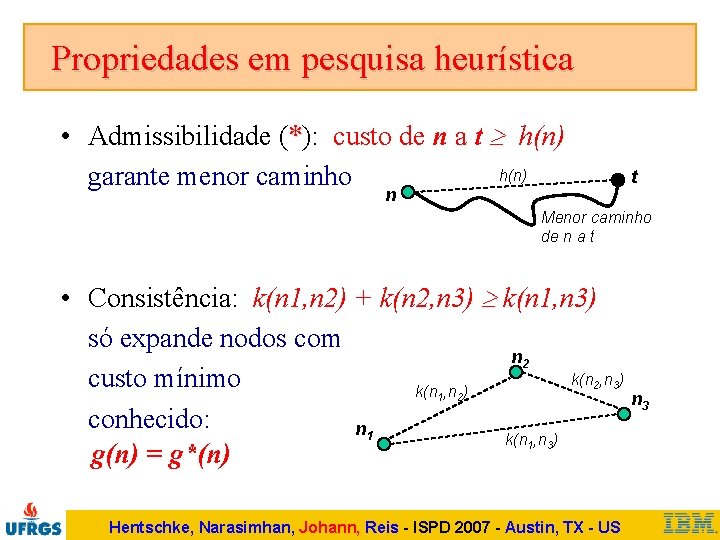
Propriedades em pesquisa heurística • Admissibilidade (*): custo de n a t h(n) garante menor caminho t n Menor caminho de n a t • Consistência: k(n 1, n 2) + k(n 2, n 3) k(n 1, n 3) só expande nodos com n 2 k(n , n ) custo mínimo k(n , n ) n 3 conhecido: n 1 k(n , n ) g(n) = g*(n) 2 1 3 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

Propriedades do Algoritmo A* • • Continuidade - sempre existe nodo Ps-t*. Perfeição - A* não entra em loop. Admissibilidade - A* encontra caminho ótimo. Condição suficiente para expansão - f(n) < Ps-t*. Condição necessária para expansão - f(n) Ps-t*. Indeterminismo em empates críticos - biasing. Monotonia - se n 2 é expandido depois de n 1 então f(n 2) f(n 1 ). • Dominância - A* mais informado expande menos. • Excelência - A* ótimo entre unidirecionais informados quando heurística é consistente e sem empates críticos. Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US

1 g=1 h=4 f =5 2 c=1 6 g=1 h=4 f =5 7 c=1 g=0 h=3 f =3 g=0 h=4 f =4 3 c=1 8 c=1 g=1 h=2 f =3 c=1 g=3 h=3 f =6 c=1 g= h= f= c=1 9 c=1 g=2 h=1 f =3 c=1 14 4 g= h= f= c=1 13 g=2 h=3 f =5 c=1 10 c=1 g= h= f= c=1 15 c=1 g= h= f= c=1 11 c=1 g= h= f= Open List: 13 Hentschke, Narasimhan, Johann, Reis - ISPD 2007 - Austin, TX - US