Maximum packings and minimum coverings of multigraphs with

Maximum packings and minimum coverings of multigraphs with paths and stars Hung-Chih Lee Department of Information Technology Ling Tung University Chun-Cheng Chen Department of Mathematics National Central University 1

Outline Introduction Packing and covering of λKn, n 2

Introduction Kn : the complete graph with n vertices. Km, n : the complete bipartite graph with parts of sizes m and n. If m = n, the complete bipartite graph is referred to as balanced. Sk (k-star) : the complete bipartite graph K 1, k. Pk (k-path) : a path on k vertices. Ck (k-cycle) : a cycle of length k. 3

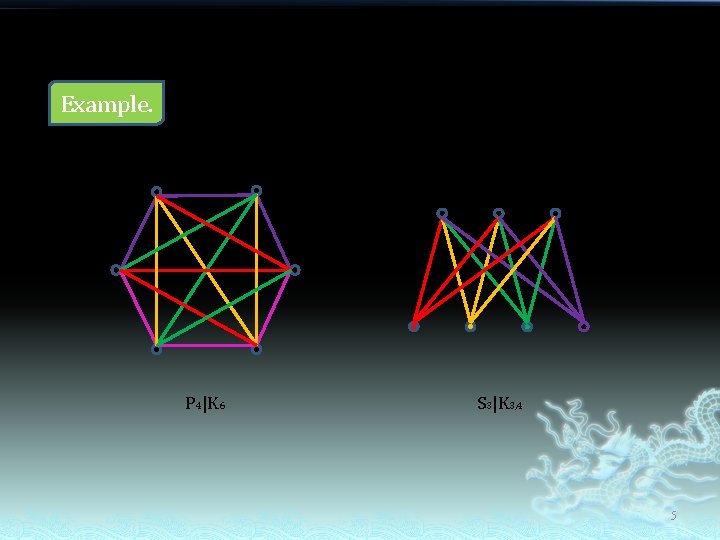
λH : the multigraph obtained from H by replacing each edge e by λ edges each having the same endpoints as e. When λ = 1, 1 H is simply written as H. A decomposition of H : a set of edge-disjoint subgraphs of H whose union is H. A G-decomposition of H : a decomposition of H in which each subgraph is isomorphic to G. If H has a G-decomposition, we say that H is Gdecomposable and write G|H. 4

Example. K 6 K 3, 4 P 4|K 6 S 3|K 3, 4 5

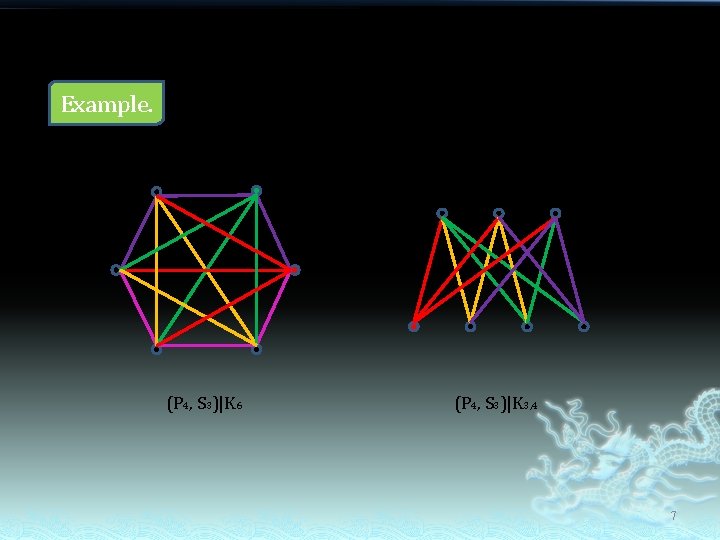
An (F, G)-decomposition of H : a decomposition of H into copies of F and G using at least one of each. If H has an (F, G)-decomposition, we say that H is (F, G)-decomposable and write (F, G)|H. 6

Example. K 6 K 3, 4 (P 4, S 3)|K 6 (P 4, S 3)|K 3, 4 7

Abueida and Daven [3] investigated the problem of (Kk, Sk)-decomposition of the complete graph Kn. [3] A. Abueida and M. Daven, Multidecompositons of the complete graph, Ars Combin. 72(2004), 17 -22. Abueida and Daven [4] investigated the problem of the (C 4, E 2)-decomposition of several graph products where E 2 denotes two vertex disjoint edges. [4] A. Abueida and M. Daven, Multidecompositions of several graph products, Graphs Combin. 29 (2013), 315 -326. Abueida and O‘Neil [7] settled the existence problem for (Ck, Sk-1)-decomposition of the complete multigraph λKn for k ∈ {3, 4, 5}. [7] A. Abueida and T. O'Neil, Multidecomposition of λKm into small cycles and claws, Bull. Inst. Combin. Appl. 49 (2007), 32 -40. 8

Priyadharsini and Muthusamy [15, 16] gave necessary and sufficient conditions for the existence of (Gn, Hn)-decompositions of λKn and λKn, n where Gn, Hn ∈ {Cn, Pn, Sn-1}. [15] H. M. Priyadharsini and A. Muthusamy, (Gm, Hm)-multifactorization of λKm, J. Com-bin. Math. Combin. Comput. 69 (2009), 145 -150. [16] H. M. Priyadharsini and A. Muthusamy, (Gm, Hm)-multidecomposition of Km, m(λ), Bull. Inst. Combin. Appl. 66 (2012), 42 -48. 9

Abueida and Daven [2] and Abueida, Daven and Roblee [5] completely determined the values of n for which λKn admits a (G, H)-decomposition where (G, H) is a graph-pair of order 4 or 5. [2] A. Abueida and M. Daven, Multidesigns for graph-pairs of order 4 and 5, Graphs Com-bin. 19 (2003), 433 -447. [5] A. Abueida, M. Daven, and K. J. Roblee, Multidesigns of the λ-fold complete graph for graph-pairs of order 4 and 5, Australas J. Combin. 32 (2005), 125 -136. 10

Abueida, Clark and Leach [1] and Abueida and Hampson [6] considered the existence of decompositions of Kn−F for the graph-pair of order 4 and 5, respectively, where F is a Hamiltonian cycle, a 1 -factor, or almost 1 -factor. [1] A. Abueida, S. Clark, and D. Leach, Multidecomposition of the complete graph into graph pairs of order 4 with various leaves, Ars Combin. 93 (2009), 403 -407. [6] A. Abueida and C. Hampson, Multidecomposition of Kn − F into graph-pairs of order 5 where F is a Hamilton cycle or an (almost) 1 -factor, Ars Combin. 97 (2010), 399 -416 Shyu [17] investigated the problem of decomposing Kn into paths and stars with k edges, giving a necessary and sufficient condition for k = 3. [17] T. -W. Shyu, Decomposition of complete graphs into paths and stars, Discrete Math. 310 (2010), 2164 -2169. 11

In [18, 19], Shyu considered the existence of a decomposition of Kn into paths and cycles with k edges, giving a necessary and sufficient condition for k ∈ { 3, 4}. [18] T. -W. Shyu, Decompositions of complete graphs into paths and cycles, Ars Combin. 97(2010), 257 -270. [19] T. -W. Shyu, Decomposition of complete graphs into paths of length three and triangles, Ars Combin. 107 (2012), 209 -224. Shyu [20] investigated the problem of decomposing Kn into cycles and stars with k edges, settling the case k = 4. [20] T. -W. Shyu, Decomposition of complete graphs into cycles and stars, Graphs Combin. 29 (2013), 301 -313. 12

In [21], Shyu considered the existence of a decomposition of Km, n into paths and stars with k edges, giving a necessary and sufficient condition for k = 3. [21] T. -W. Shyu, Decomposition of complete bipartite graphs into paths and stars with same number of edges, Discrete Math. 313 (2013), 865 -871. Lee [12] and Lee and Lin [13] established necessary and sufficient conditions for the existence of (Ck, Sk)decompositions of the complete bipartite graph and the complete bipartite graph with a 1 -factor removed, respectively. [12] H. -C. Lee, Multidecompositions of complete bipartite graphs into cycles and stars, Ars Combin. 108 (2013), 355 -364. [13] H. -C. Lee and J. -J. Lin, Decomposition of the complete bipartite graph with a 1 factor removed into cycles and stars, Discrete Math. 313 (2013), 2354 -2358. 13

When a multigraph H does not admit an (F, G)decomposition, two natural questions arise : (1) What is the minimum number of edges needed to be removed from the edge set of H so that the resulting graph is (F, G)-decomposable? (2) What is the minimum number of edges needed to be added to the edge set of H so that the resulting graph is (F, G)-decomposable? These questions are respectively called the maximum packing problem and the minimum covering problem of H with F and G. 14

Let F, G, and H be multigraphs. For subgraphs L and R of H. An (F, G)-packing ((F, G)-covering) of H with leave L (padding R) is an (F, G)-decomposition of H−E(L) (H+E(R)). An (F, G)-packing ((F, G)-covering) of H with the largest (smallest) cardinality is a maximum (F, G)-packing (minimum (F, G)-covering) of H, and its cardinality is the (F, G)-packing number ((F, G)-covering number) of H, denoted by p(H; F, G) (c(H; F, G)). An (F, G)-decomposition of H is a maximum (F, G)-packing (minimum (F, G)-covering) with leave (padding) the empty graph. 15

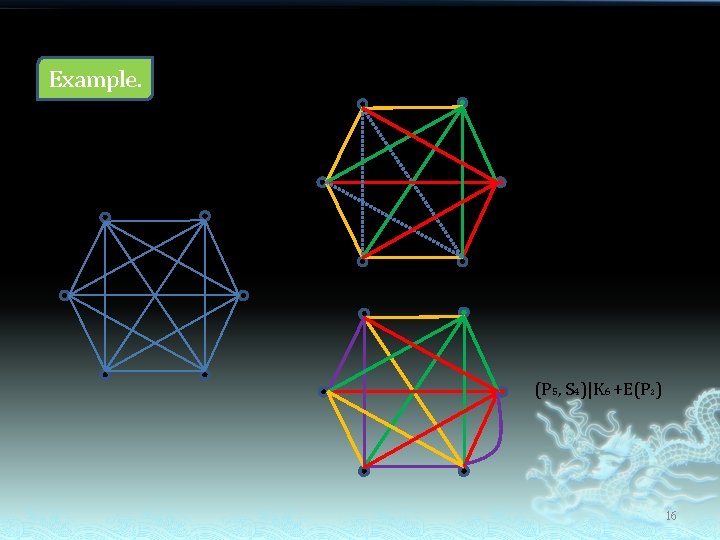
Example. K 6 (P 5, S 4)|K 6 –E(P 4) (P 5, S 4)|K 6 +E(P 2) 16

Abueida and Daven [3] obtained the maximum packing and the minimum covering of the complete graph Kn with (Kk, Sk). [3] A. Abueida and M. Daven, Multidecompositons of the complete graph, Ars Combin. 72(2004), 17 -22. Abueida and Daven [2] and Abueida, Daven and Roblee [5] gave the maximum packing and the minimum covering of Kn and λKn with G and H, respectively, where (G, H) is a graph-pair of order 4 or 5. [2] A. Abueida and M. Daven, Multidesigns for graph-pairs of order 4 and 5, Graphs Com-bin. 19 (2003), 433 -447. [5] A. Abueida, M. Daven, and K. J. Roblee, Multidesigns of the λ-fold complete graph for graph-pairs of order 4 and 5, Australas J. Combin. 32 (2005), 125 -136. 17

Packing and covering of λKn Let G be a multigraph. The degree of a vertex x of G (deg. G(x)) : the number of edges incident with x. The center of Sk : the vertex of degree k in Sk. The endvertex of Sk : the vertex of degree 1 in Sk. (x; y 1, y 2, …, yk) : the Sk with center x and endvertices y 1, y 2, …, yk. 19

v 1 v 2… vk : the Pk through vertices v 1, v 2, …, vk in order, and the vertices v 1 and vk are referred to as its origin and terminus. If P = x 1 x 2…xt, Q = y 1 y 2…ys and xt = y 1, then P + Q = x 1 x 2…xty 2…ys. Pk(v 1, vk) : a Pk with origin v 1 and terminus vk. 20

G[U] : the subgraph of G induced by U. G[U, W] : the maximal bipartite subgraph of G with bipartition (U, W). When G 1, G 2, …, Gt are multigraphs, not necessarily disjoint. 21

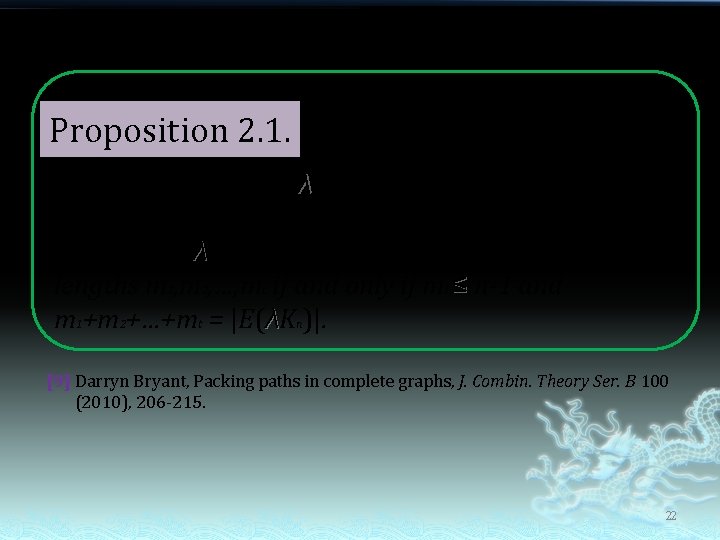
Proposition 2. 1. For positive integers λ, n, and t, and any sequence m 1, m 2, …, mt of positive integers, the complete multigraph λKn can be decomposed into paths of lengths m 1, m 2, …, mt if and only if mi ≤ n-1 and m 1+m 2+…+mt = |E(λKn)|. [9] Darryn Bryant, Packing paths in complete graphs, J. Combin. Theory Ser. B 100 (2010), 206 -215. 22

Proposition 2. 2. [8] J. Bosák, Decompositions of Graphs, Kluwer, Dordrecht, Netherlands, 1990. [10] P. Hell and A. Rosa, Graph decompositions, handcuffed prisoners and balanced P-designs, Discrete Math. 2 (1972), 229 -252. 23

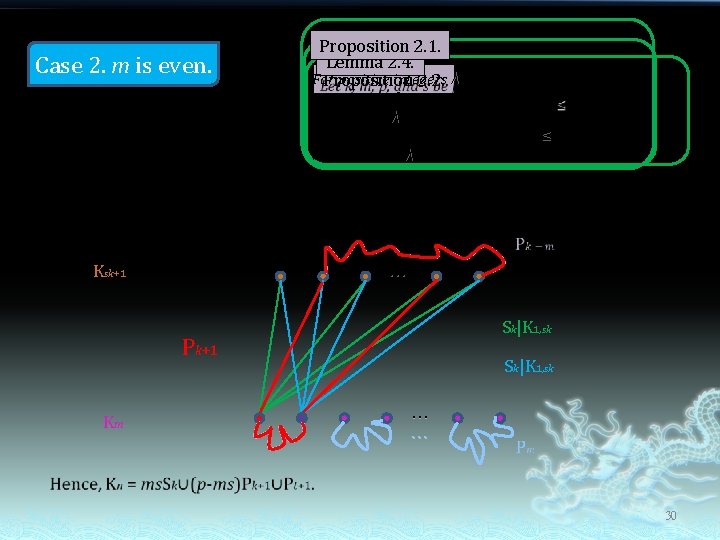
Theorem 2. 5. Let n and k be positive integers and let t be a nonnegative integer with k ≥ 3, n ≥ k + 2, and t ≤ k-1. If |E(Kn)| ≡ t (mod k), then Kn has a (Pk+1, Sk)-packing with leave Pt+1. Proof. Let n = qk+r and |E(Kn)| = pk+t with integers q, p, r and 0 ≤ r ≤ k -1. Now we consider the case r ≠ 1, we set n = m + sk + 1 where m and s are positive integers with 1 ≤ m ≤ k-1. Case 1. m is odd. Case 2. m is even. 25

Case 2. m is even. Proposition 2. 1. Lemma 2. 4. For positive integers Proposition 2. 2. λ, n, and t, and any sequence m 1, m 2, …, mt of positive integers, the complete multigraph λKn can be decomposed into paths of lengths m 1, m 2, …, mt if and only if mi ≤ n-1 and m 1+ m 2+…+mt = |E(λKn)|. … Ksk+1 Sk|K 1, sk Pk+1 Km Sk|K 1, sk … … 30

Theorem 2. 6. Let λ, n and k be positive integers and let t be a nonnegative integer with k ≥ 3, n ≥ k+2, and t ≤ k-1. If |E(λKn)| ≡ t (mod k), then λKn has a (Pk+1, Sk)-packing with leave Pt+1. 31

Corollary 2. 7. 33

For positive integers k, n, and t with k ≤ n-1 and t ≤ k-1. If λKn has a (Pk+1, Sk)-packing with leave Pt+1, then it has a (Pk+1, Sk)covering with padding Pk-t+1. Theorem 2. 8. 38

Packing and covering of λKn, n (v 1, v 2, …, vk) : the k-cycle of G through vertices v 1, v 2, …, vk in order. μ(uv) : the number of edges of G joining u and v. A central function c from V(G) to the set of nonnegative integers is defined as follows : for each v∈ V(G), c(v) is the number of Sk in the decomposition whose center is v. 39

Proposition 3. 1. [11] D. G. Hoffman, The real truth about star designs, Discrete Math. 284 (2004), 177 -180. 40

Lemma 3. 4. Lemma 3. 6. 44

Proof of Lemma 3. 4. Let n = k + r. The assumption k < n < 2 k implies 0 < r < k. Packing. Lemma 3. 3. If λ and k are positive integers with k ≥ 2, then λKk, k is (Pk+1, Sk)decomposable. By Lemma 3. 3. ⇒ (Pk+1, Sk) |Kk, k leave 45

Covering Define a (k + 1)-path P as follows: H = λK λ n, n - E(P) + E(P’). … … P P’ … … k is odd. … … s is odd. … … … … 46

Claim. Sk|H Proposition 3. 1. 47

Theorem 3. 7. Corollary 3. 8. 48

[1] A. Abueida, S. Clark, and D. Leach, Multidecomposition of the complete graph into graph pairs of order 4 with various leaves, Ars Combin. 93 (2009), 403 -407. [2] A. Abueida and M. Daven, Multidesigns for graph-pairs of order 4 and 5, Graphs Com-bin. 19 (2003), 433 -447. [3] A. Abueida and M. Daven, Multidecompositons of the complete graph, Ars Combin. 72(2004), 17 -22. [4] A. Abueida and M. Daven, Multidecompositions of several graph products, Graphs Combin. 29 (2013), 315 -326. [5] A. Abueida, M. Daven, and K. J. Roblee, Multidesigns of the λ-fold complete graph for graph-pairs of order 4 and 5, Australas J. Combin. 32 (2005), 125 -136. [6] A. Abueida and C. Hampson, Multidecomposition of Kn − F into graph-pairs of order 5 where F is a Hamilton cycle or an (almost) 1 -factor, Ars Combin. 97 (2010), 399 -416 [7] A. Abueida and T. O'Neil, Multidecomposition of λKm into small cycles and claws, Bull. Inst. Combin. Appl. 49 (2007), 32 -40. [8] J. Bosák, Decompositions of Graphs, Kluwer, Dordrecht, Netherlands, 1990.

[9] Darryn Bryant, Packing paths in complete graphs, J. Combin. Theory Ser. B 100 (2010), 206 -215. [10] P. Hell and A. Rosa, Graph decompositions, handcuffed prisoners and balanced P-designs, Discrete Math. 2 (1972), 229 -252. [11] D. G. Hoffman, The real truth about star designs, Discrete Math. 284 (2004), 177 -180. [12] H. -C. Lee, Multidecompositions of complete bipartite graphs into cycles and stars, Ars Combin. 108 (2013), 355 -364. [13] H. -C. Lee and J. -J. Lin, Decomposition of the complete bipartite graph with a 1 factor removed into cycles and stars, Discrete Math. 313 (2013), 2354 -2358. [14] C. A. Parker, Complete bipartite graph path decompositions, Ph. D. Thesis, Auburn Uni-versity, Auburn, Alabama, 1998. [15] H. M. Priyadharsini and A. Muthusamy, (Gm, Hm)-multifactorization of λKm, J. Com-bin. Math. Combin. Comput. 69 (2009), 145 -150. [16] H. M. Priyadharsini and A. Muthusamy, (Gm, Hm)-multidecomposition of Km, m(λ), Bull. Inst. Combin. Appl. 66 (2012), 42 -48.

[17] T. -W. Shyu, Decomposition of complete graphs into paths and stars, Discrete Math. 310 (2010), 2164 -2169. [18] T. -W. Shyu, Decompositions of complete graphs into paths and cycles, Ars Combin. 97(2010), 257 -270. [19] T. -W. Shyu, Decomposition of complete graphs into paths of length three and triangles, Ars Combin. 107 (2012), 209 -224. [20] T. -W. Shyu, Decomposition of complete graphs into cycles and stars, Graphs Combin. 29 (2013), 301 -313. [21] T. -W. Shyu, Decomposition of complete bipartite graphs into paths and stars with same number of edges, Discrete Math. 313 (2013), 865 -871.

Thank you for your listening. 52