MAXIMUM LIKELIHOOD USED TO CALCULATE CONFIDENCE IN ASSOCIATION

MAXIMUM LIKELIHOOD USED TO CALCULATE CONFIDENCE IN ASSOCIATION RULE MINING By Arijit Chatterjee Dr. William Perrizo Computer Science Department North Dakota State University

Contents • Data Mining • Applications • Association Rule Mining • Market Basket Analysis • Statistical Estimation and Maximum Likelihood Function • MLF used to calculate confidence and collective confidence of Association Rules

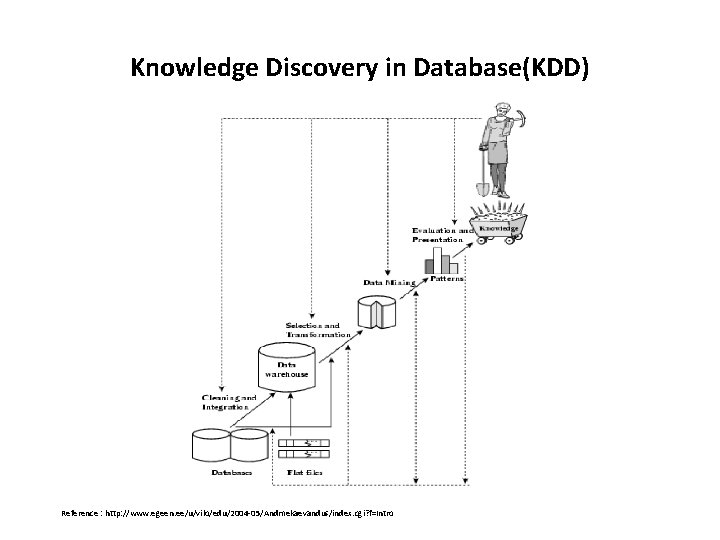
Data Mining § Data mining is becoming an important tool and a highly potent process capable of discovering and extracting important information from huge volumes of raw data. § Data Mining is sometimes erroneously treated synonymously to the broader process of Knowledge and Data Discovery (KDD).

Knowledge Discovery in Database(KDD) Reference : http: //www. egeen. ee/u/vilo/edu/2004 -05/Andmekaevandus/index. cgi? f=Intro

Applications of Data Mining • Business • Science and Engineering • Spatial Data Mining • Surveillance • Games

Data Mining Tasks § Characterization – General characteristics and features of a specific class of data. § Discrimination – Characteristics in comparison with contrasting classes. § Classification – Using training dataset with known class samples to come up with a model that predicts the unknown class labels of new samples.

continued…. . § Clustering – Process of grouping data objects into different clusters. § Outlier Detection – Process of studying the objects that lie scattered around a dataset. § Association Rule Mining – Popular method in finding interesting relations between variables in large databases.

Association Rules Association rule mining finds interesting associations and/or correlationships among large set of data items. Association rules show attribute value conditions that occur frequently together in a given dataset. A typical and widely-used example of association rule mining is Market Basket Analysis.

Market Basket Analysis Definition: Market Basket Analysis sometimes also referred to as Association Analysis is a mathematical modeling technique based upon theory that if you buy certain group of items , you are likely to buy another group of items. Usage: § Understanding behavior of shoppers Basket data consist of collection of transaction date and items bought in a transaction • Item set § Retail organizations interested in generating qualified decisions and strategy based on analysis of transaction data • what to put on sale, how to place merchandise on shelves for maximizing profit, customer segmentation based on buying pattern

Rules and Examples • Association rules provide information of this type in the form of "if-then" statements. These rules are computed from the data and, unlike the ifthen rules of logic, association rules are probabilistic in nature. Rule form: LHS -> RHS – IF a customer buys diapers, THEN they also buy beer • diapers -> beer – “Transactions in which bread and butter are purchased also purchased milk” • bread butter milk • In association analysis the antecedent and consequent are sets of items (called item sets) that are disjoint (do not have any items in common).

How can Maximum Likelihood Function be used to Calculate Confidence Of Association Rules In Market Baskets ?

Statistical Estimation Theory of Estimation requires a random sample x 1, x 2…………………xn on a variable x whose distribution in the population involves an unknown parameter . It is required to find an estimate of on the basis of random values. The estimation is done in two different ways: i) Point Estimation and ii) Interval Estimation. In Point Estimation, the estimated value is given by a single quantity which is a function of sample observations (i. e. statistic). This function is called the ‘estimator’ of the parameter and the value of the estimator in a particular example is called an ‘estimate’. Consider, x 1, x 2…………………xn be a random sample from a population with probability mass function, f(x, ), where is the parameter. Then the joint distribution of the sample observations denoted as L is defined by: L = f(x 1, ) f(x 2, ) f(x 3, ) f(x 4, ). . f(xn, )

Method of Maximum Likelihood The method of Maximum Likelihood consists in choosing as an estimator of and that statistic when substituted for maximizes the likelihood function L. Such a statistic is called the Maximum Likelihood Estimator (M. L. E). Since log L is maximum when L is maximum the maximum likelihood estimator of is obtained by maximizing log L. This is achieved by differentiating log L partially with respect to and using the two relations as listed in the following: The Two Conditions: 1. log L = 0 when = 0 2. 2 log L < 0 when = 0 2

Probability Distribution of a random variable is a statement specifying the set of its possible values together with their respective probabilities. When a random experiment is theoretically assumed to serve as a model, the probabilities can be given as a function of the random variable. The probability distribution concerned is then generally known as theoretical distribution. The Binomial Distribution is a discrete probability distribution and is defined by the p. m. f f(x) = n. Cx px (1 -p)n-x (x = 0, 1, 2, ………n) where p is the probability of success.

Example : If a supermarket database has 100, 000 point of sale transactions, out of which 4, 000 include both items A and B and 1000 of these include item C then the association rule “If A and B are purchased then C is purchased in the same trip” has a support of 1% and a confidence of 25%.

Can we use the Maximum Likelihood Function to calculate the confidence of an Association Rule ? Let p be the probability that when items A and B are purchased then item C is also purchased. 4000 of the transactions have items A and B and out of those 1000 include item C. So the probability that item C occurs 1000 times in 4000 trials is 4000 C 1000 p 1000 (1 -p) 4000 -1000. Since this is a single association rule then the likelihood function is given by L = 4000 C 1000 p 1000 (1 -p) 4000 -1000 = 4000 C 1000 p 1000 (1 -p) 3000 log L = log (4000 C 1000) + 1000 log p + 3000 log (1 -p) Differentiating with respect to p on both sides : Log L = 1000/p – 3000/ (1 -p) P The maximum likelihood estimator po is therefore obtained by solving 1000/ po – 3000/ (1 - po) = 0 Solving , po =. 25

Using Maximum Likelihood Function to calculate collective Confidence of Association Rules Let’s assume that out of n items in which A & B are together purchased x number of those items contain item C. If p is the probability of the item C to be occurring then the likelihood function of this rule can be expressed as follows: L 1 = n. Cx px (1 -p)n-x where (x = 0, 1, 2, ………n) . . . (i) If we have another independent transaction which shows that “When items D & E are purchased then also item C is also purchased in the same trip”. If out of m items in which items D & E are together purchased y number of those items contain C then the likelihood function of this association rule can be expressed as follows: L 2 = m. Cy py (1 -p)m-y where (y = 0, 1, 2, ………m) . . . (ii) Based on both transactions the collective confidence of both of the association rules can be thought to be the maximum likelihood estimate of buying item C whenever a transaction happens.

The likelihood function L is given by the product of these likelihood functions. L = L 1. L 2 = n. Cx px (1 -p)n-x . m. Cy py (1 -p)m-y =( n. Cx m. Cy ). px+y. (1 -p)[(m+n)-(x+y)] log L=log( n. Cx m. Cy ) + (x+y)log p +[(m+n)-(x+y)]log(1 -p) Differentiating with respect to p on both sides: Log L = (x+y)/p – [(m+n)-(x+y)] / (1 -p) P The maximum likelihood estimator po is therefore obtained by solving (x+y)/ po – [(m+n)-(x+y)] / (1 - po) = 0 Solving, po = (x+y) / (m+n) The collective confidence of selecting item C from the association rules is thus found to be (x+y) / (m+n).