Maximum Likelihood Linear Regression for Speaker Adaptation of

Maximum Likelihood Linear Regression for Speaker Adaptation of Continuous Density Hidden Markov Models C. J. Leggetter and P. C. Woodland Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB 2 1 PZ, U. K. Computer Speech and Language (1995) Present by Hsu Ting-Wei 2006. 03. 16

Introduction Say: “Hello!” Speaker HMM Models • Speaker adaptation techniques fall into two main categories: – Speaker normalization • The input speech is normalized to match the speaker that the system is trained to model – Model adaptation techniques • The parameters of the model set are adjusted to improve the modeling of the new speaker • MAP method – Only update the parameters of models which are observed in the adaptation data • MLLR method (Maximum Likelihood Linear Regression) – All model states can be adapted even if no model-specific data is available 2

MLLR’s adaptation approach • This method requires an initial speaker independent continuous density HMM system • MLLR takes some adaptation data from a new speaker and updates the model mean parameters to maximize the likelihood of the adaptation data • The other HMM parameters are not adapted since the main differences between speakers are assumed to be characterized by the means 3

MLLR’s adaptation approach (cont. ) • Consider the case of a continuous density HMM system with Gaussian output distributions. • A particular distribution s , is characterized by a mean vector , and a covariance matrix • Given a parameterized speech frame vector , the probability density of that vector being generated by distribution s is where n is the dimension of the observation vector S speech frame vector 4

MLLR’s adaptation approach (cont. ) • We use the following equation Original. . • We can simply it n*(n+1)*1 where transformation matrices extended mean vector 要調適的分佈的mean值 所串起的向量 offset = 1, include an offset in the regression offset = 0, ignore offsets 若調適語者的錄音環境與初始模型錄音環境不同時， 可以加入的一項參數 [參考資料] • So the probability density function for the adapted system becomes (1) 5

MLLR’s adaptation approach (cont. ) • The transformation matrices are calculated to maximize the likelihood of the adaptation data • The transformation matrices can be implemented using the forward–backward algorithm • A more general approach is adopted in which the same transformations matrix is used for several distributions. • If some of the distributions are not observed in the adaptation data, a transformation may still be applied (global transformation) 6

Estimation of MLLR regression matrices • 1. Definition of auxiliary function S speech frame vector objective function E-step 7

Estimation of MLLR regression matrices (cont. ) • 2. Maximization of auxiliary function (2) only related with mean (3) 8

Estimation of MLLR regression matrices (cont. ) • 2. Maximization of auxiliary function (cont. ) (4) expanding this term 9

Estimation of MLLR regression matrices (cont. ) • 2. Maximization of auxiliary function (cont. ) 10

Estimation of MLLR regression matrices (cont. ) • 2. Maximization of auxiliary function (cont. ) M-step <= 估測 的general form (5) 11

Estimation of MLLR regression matrices (cont. ) • 3. Re-estimation formula for tied regression matrices [(n+1)*1][1*(n+1)] =(n+1) *(n+1) 當調適語料不夠多時，可以將調適語料中相關性較大的狀態分為 同一類，利用在同一類別中所收集到的語料來估測Ws。 12

Estimation of MLLR regression matrices (cont. ) ? • 3. Re-estimation formula for tied regression matrices (cont. ) (7)is denoted by n*(n+1) matrix Y (7)is denoted by n*(n+1) matrix Z 13

Special cases of MLLR • 1. Least squares regression YX’ (XX’) 14

Special cases of MLLR (cont. ) • 1. Least squares regression (cont. ) 15

Special cases of MLLR (cont. ) • 2. Single variable linear regression 16

Special cases of MLLR (cont. ) • 2. Single variable linear regression (cont. ) M-step 17

Defining regression classes • When regression matrices are tied across mixture components, each matrix is associated with many mixture components. • For the tied approach to be effective it is desirable to put all the mixture components which will use similar transforms into the same class. • Two approaches for defining regression classes were considered: – Based on broad phonetic classes • All mixture components in any model representing the same broad phonetic class (e. g. fricatives, nasals, etc. ) were placed in the same regression class. – Based on clustering of mixture components • The mixture components were compared using a likelihood measure and similar components placed in the same regression class. 18

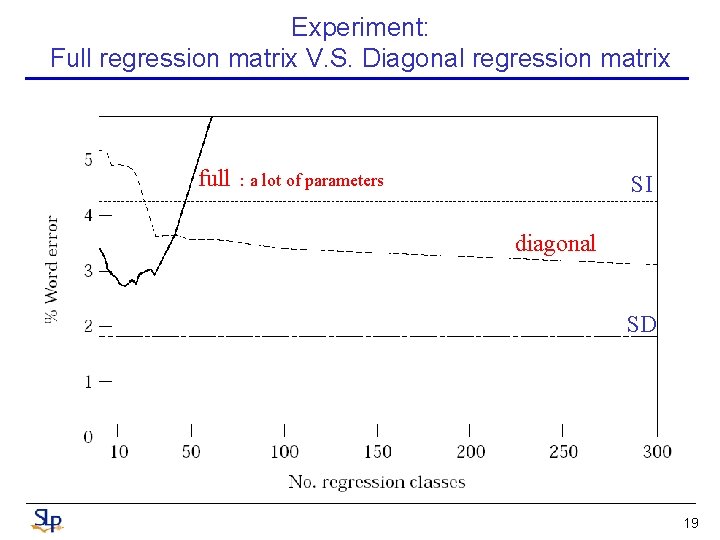
Experiment: Full regression matrix V. S. Diagonal regression matrix full : a lot of parameters SI diagonal SD 19

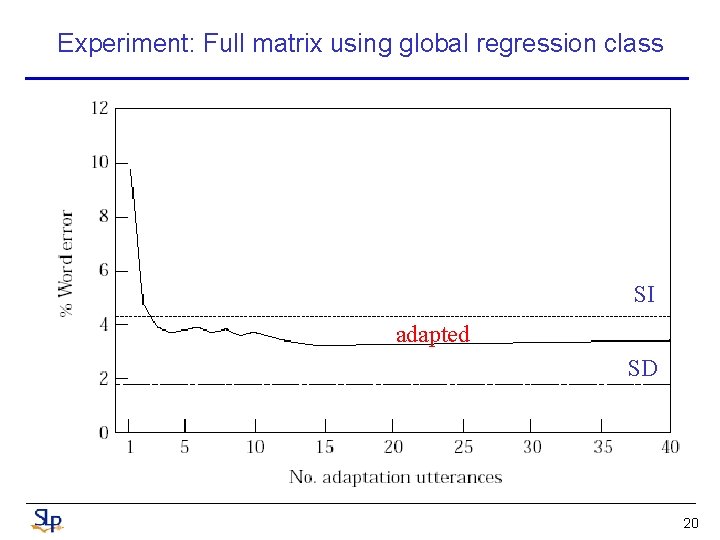
Experiment: Full matrix using global regression class SI adapted SD 20

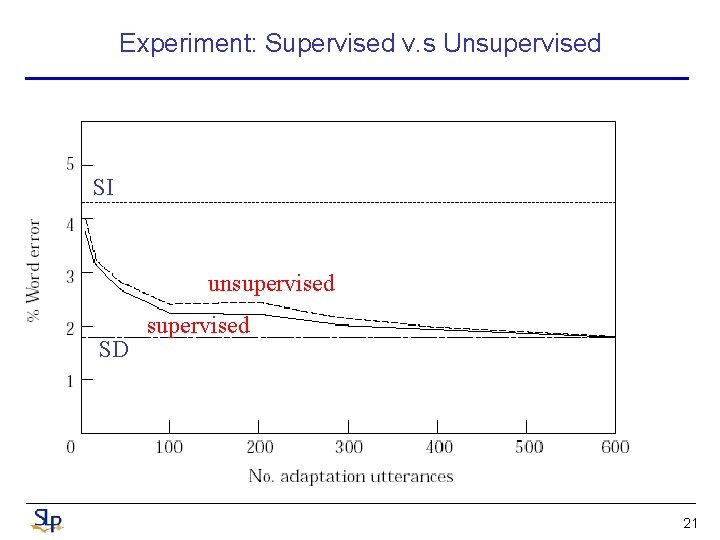
Experiment: Supervised v. s Unsupervised SI unsupervised SD supervised 21

Conclusion • MLLR can be applied to continuous density HMMs with a large number of Gaussians and is effective with small amounts of adaptation data. 22