Maximum Likelihood Estimation Multivariate Normal distribution The Method

Maximum Likelihood Estimation Multivariate Normal distribution

The Method of Maximum Likelihood Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q 1, … , qp) where q = (q 1, … , qp) are unknown parameters assumed to lie in W (a subset of p-dimensional space). We want to estimate the parametersq 1, … , qp

Definition: The Likelihood function Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q 1, … , qp) Then given the data the Likelihood function is defined to be = L(q 1, … , qp) = f(x 1, … , xn ; q 1, … , qp) Note: the domain of L(q 1, … , qp) is the set W.

Definition: Maximum Likelihood Estimators Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q 1, … , qp) Then the Likelihood function is defined to be = L(q 1, … , qp) = f(x 1, … , xn ; q 1, … , qp) and the Maximum Likelihood estimators of the parameters q 1, … , qp are the values that maximize = L(q 1, … , qp)

i. e. the Maximum Likelihood estimators of the parameters q 1, … , qp are the values Such that Note: is equivalent to maximizing the log-likelihood function

The Multivariate Normal Distribution Maximum Likelihood Estiamtion

denote a sample (independent) Let from the p-variate normal distribution with mean vector and covariance matrix Note:

The matrix is called the data matrix.
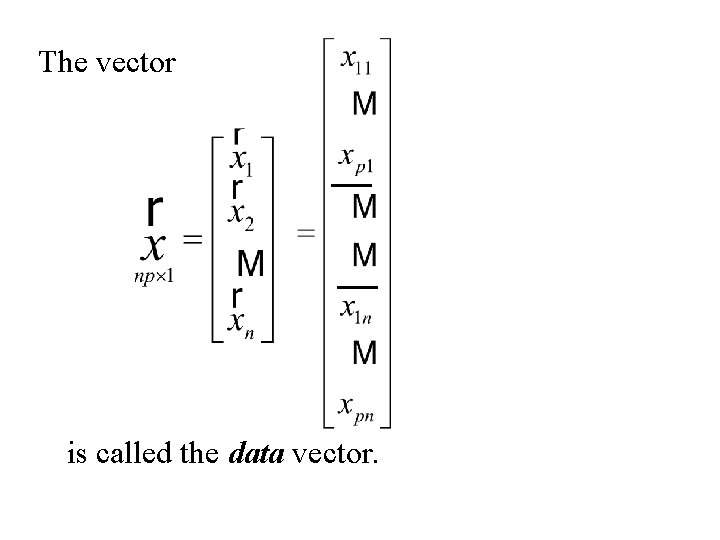
The vector is called the data vector.

The mean vector

The vector is called the sample mean vector note
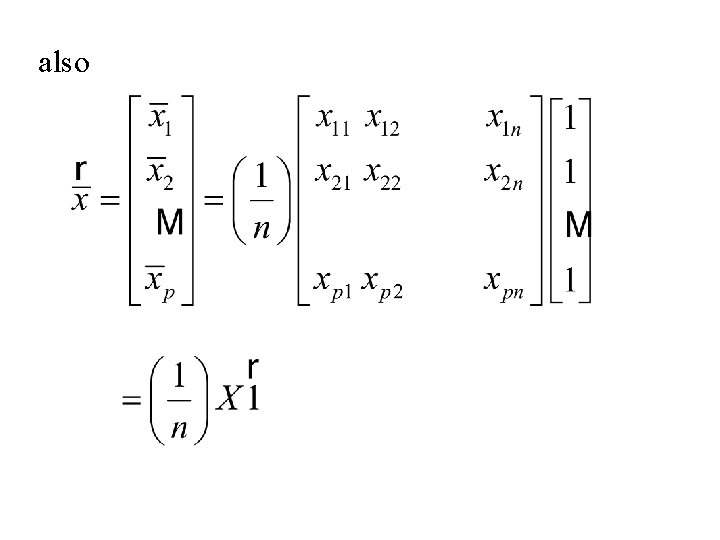
also
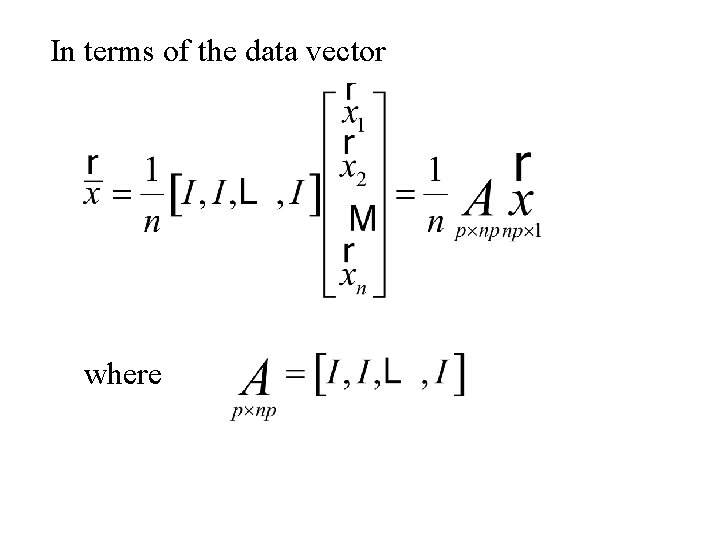
In terms of the data vector where
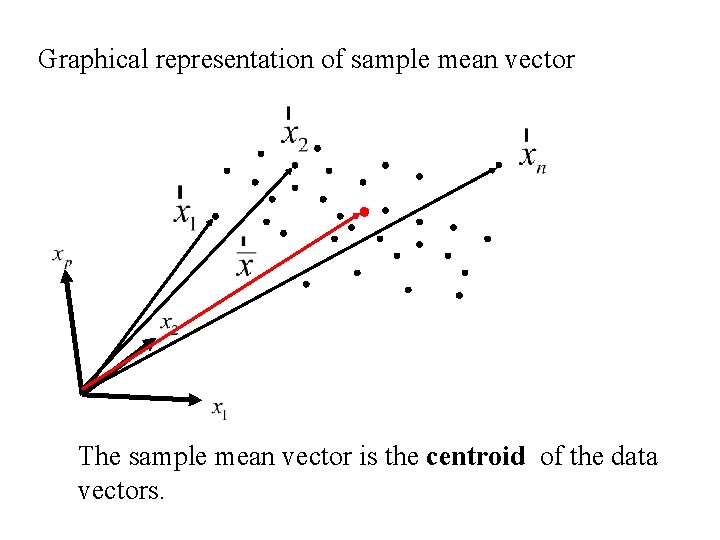
Graphical representation of sample mean vector The sample mean vector is the centroid of the data vectors.

The Sample Covariance matrix

The sample covariance matrix: where

There are different ways of representing sample covariance matrix:
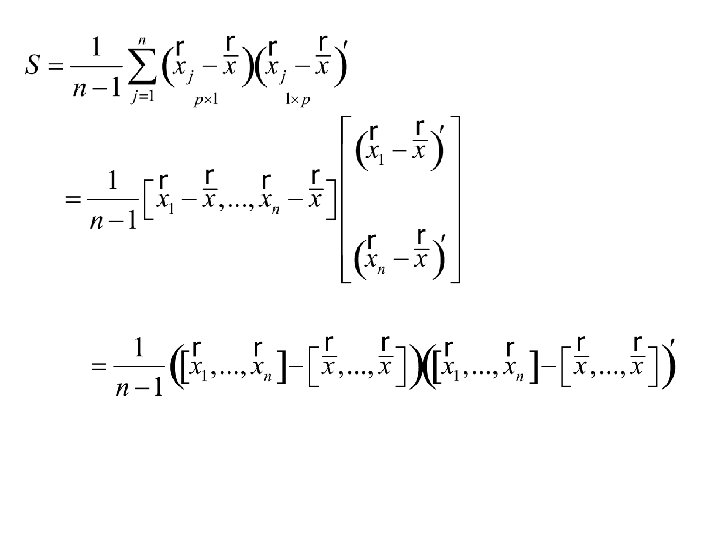
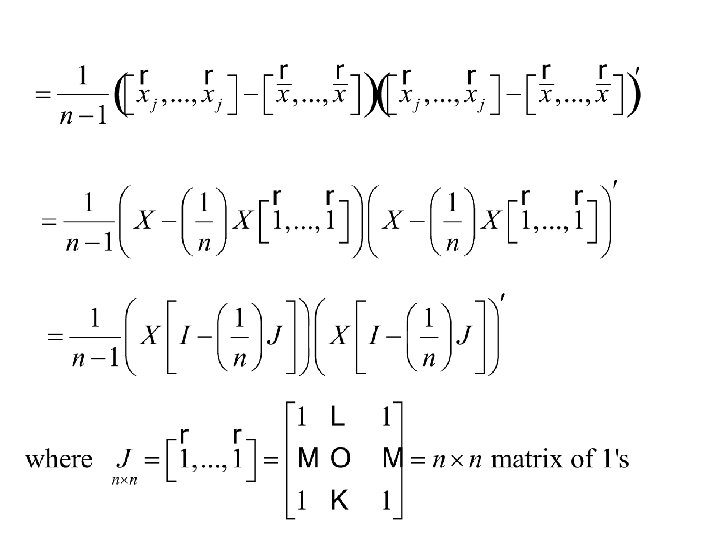
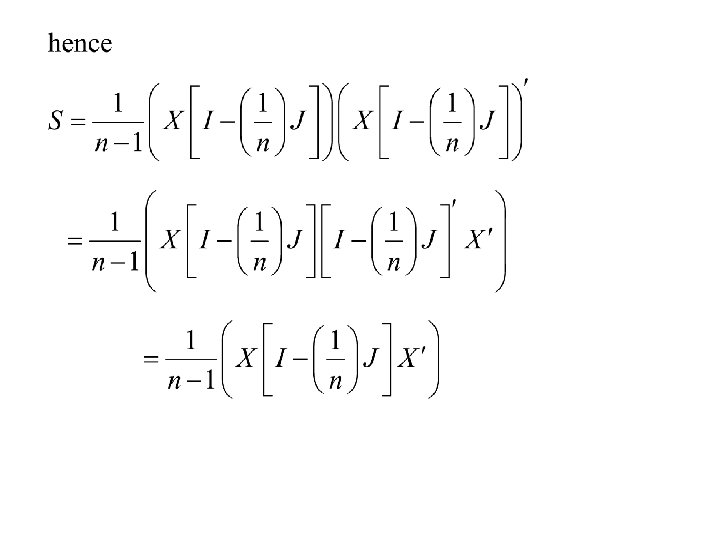

Maximum Likelihood Estimation Multivariate Normal distribution

Let denote a sample (independent) from the p-variate normal distribution with mean vector and covariance matrix Then the joint density function of is:

The Likelihood function is: and the Log-likelihood function is:

To find the Maximum Likelihood estimators of we need to find to maximize or equivalently maximize
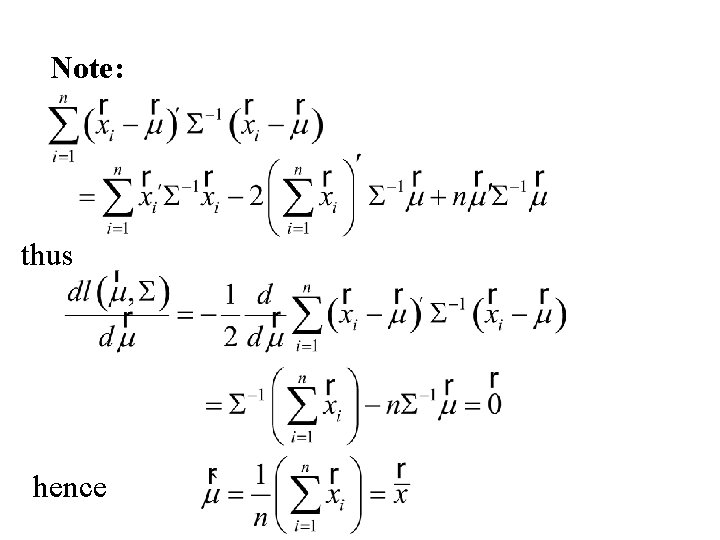
Note: thus hence
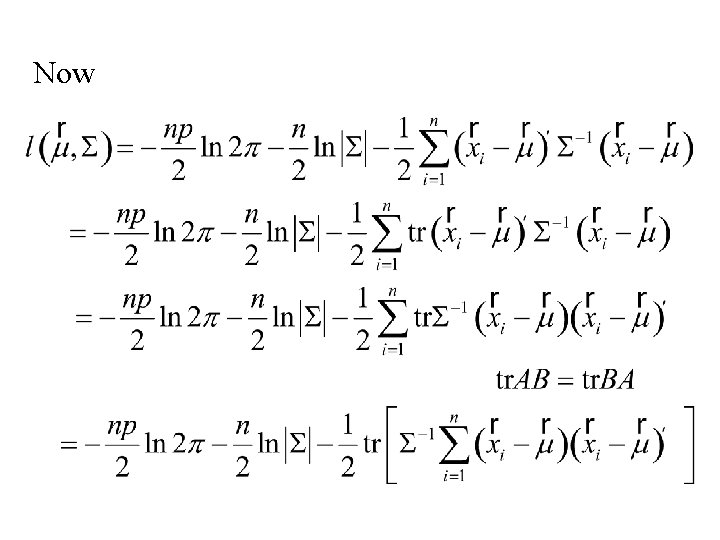
Now
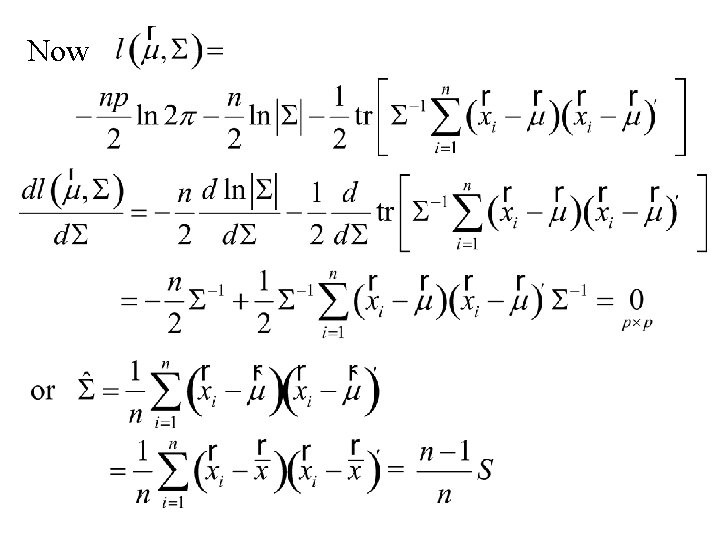
Now

Summary: the Maximum Likelihood estimators of are and

Sampling distribution of the MLE’s

Note The joint density function of is:

This distribution is np-variate normal with mean vector

Thus the distribution of is p-variate normal with mean vector
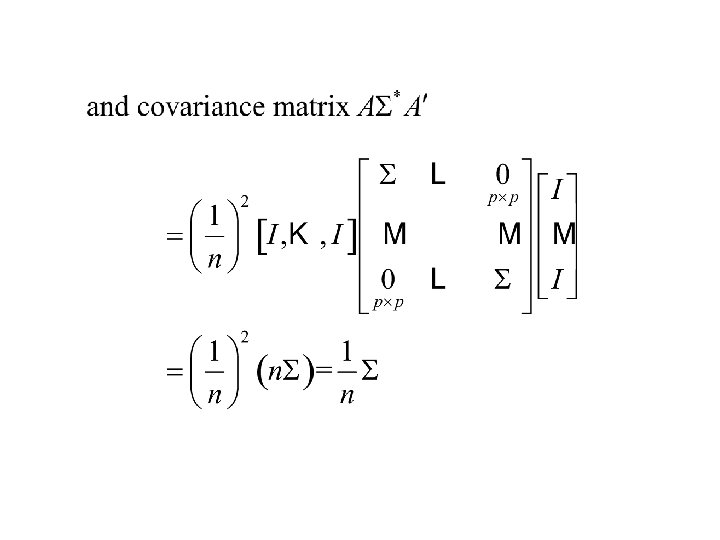

Summary The sampling distribution of is p-variate normal with

The sampling distribution of the sample covariance matrix S and

The Wishart distribution A multivariate generalization of the c 2 distribution

Definition: the p-variate Wishart distribution Let be k independent random p-vectors Each having a p-variate normal distribution with Then U is said to have the p-variate Wishart distribution with k degrees of freedom

The density ot the p-variate Wishart distribution Suppose Then the joint density of U is: where Gp(·) is the multivariate gamma function. It can be easily checked that when p = 1 and S = 1 then the Wishart distribution becomes the c 2 distribution with k degrees of freedom.

Theorem Suppose then Corollary 1: Corollary 2: Proof

Theorem Suppose are independent, then Theorem Suppose then are independent and

Theorem Let be a sample from then Theorem Let then be a sample from

Theorem Proof etc

Theorem Let be a sample from then is independent of Proof be orthogonal Then
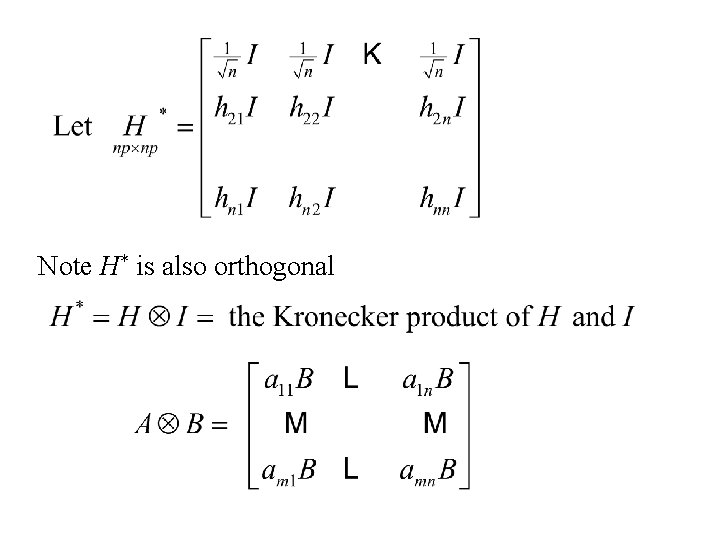
Note H* is also orthogonal

Properties of Kronecker-product
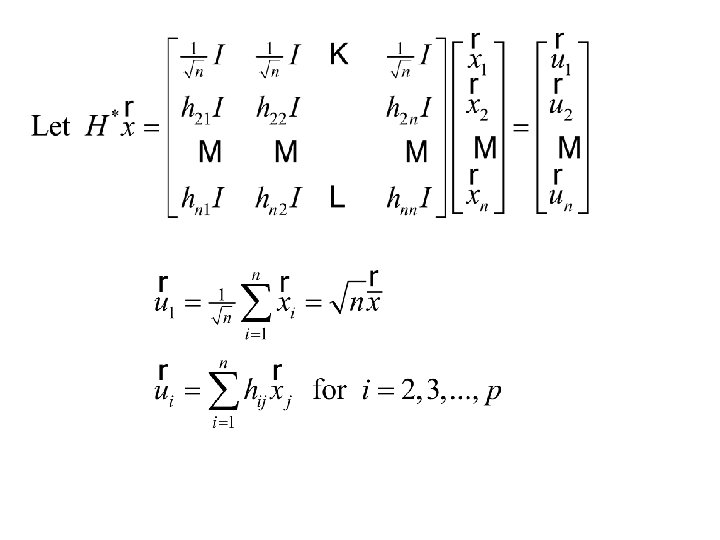


This the distribution of is np-variate normal with mean vector

Thus the joint distribution of is np-variate normal with mean vector

Thus the joint distribution of is np-variate normal with mean vector

Summary: Sampling distribution of MLE’s for multivatiate Normal distribution Let then and be a sample from
- Slides: 51