Maximum Flows Corman book Max Flow Network Max

Maximum Flows Corman book

Max Flow Network Max flow network: G = (V, E, s, t, u). – (V, E) = directed graph, no parallel arcs. – Two distinguished nodes: s = source, t = sink. – c(e) = capacity of arc e. 10 s Capacity 5 15 2 9 5 4 15 15 10 3 8 6 10 4 6 15 10 4 30 7 t
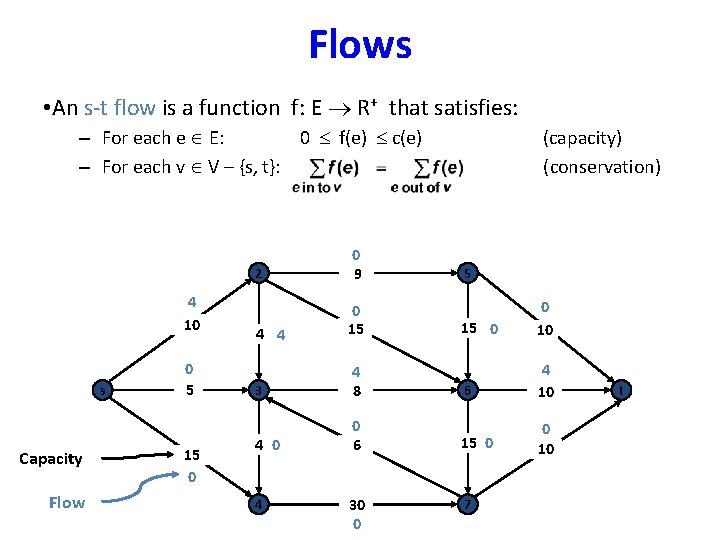
Flows • An s-t flow is a function f: E R+ that satisfies: – For each e E: 0 f(e) c(e) – For each v V – {s, t}: 4 10 s Capacity Flow 0 5 15 0 2 0 9 4 4 0 15 3 4 8 4 0 0 6 4 30 0 (capacity) (conservation) 5 15 0 0 10 6 4 10 15 0 0 10 7 t
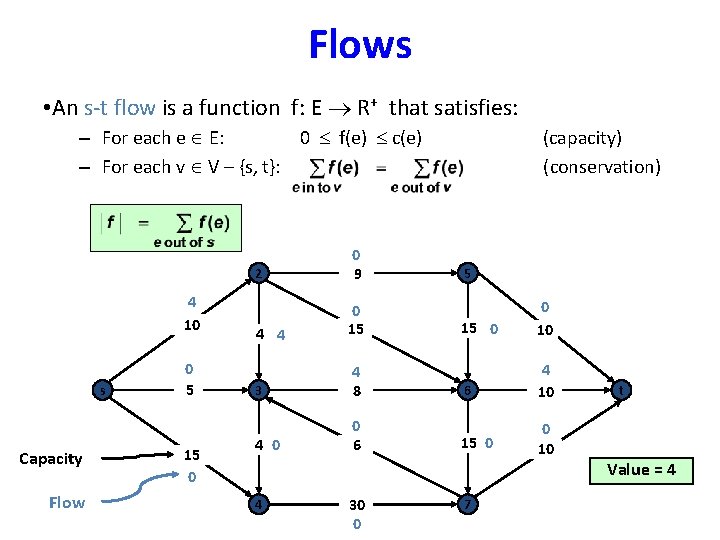
Flows • An s-t flow is a function f: E R+ that satisfies: – For each e E: 0 f(e) c(e) – For each v V – {s, t}: 4 10 s Capacity Flow 0 5 15 0 2 0 9 4 4 0 15 3 4 8 4 0 0 6 4 30 0 (capacity) (conservation) 5 15 0 0 10 6 4 10 15 0 0 10 7 t Value = 4
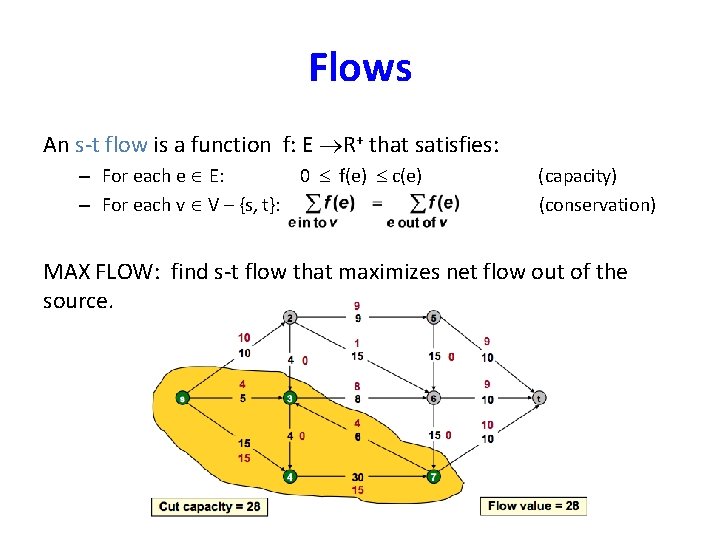
Flows An s-t flow is a function f: E R+ that satisfies: – For each e E: 0 f(e) c(e) – For each v V – {s, t}: (capacity) (conservation) MAX FLOW: find s-t flow that maximizes net flow out of the source.
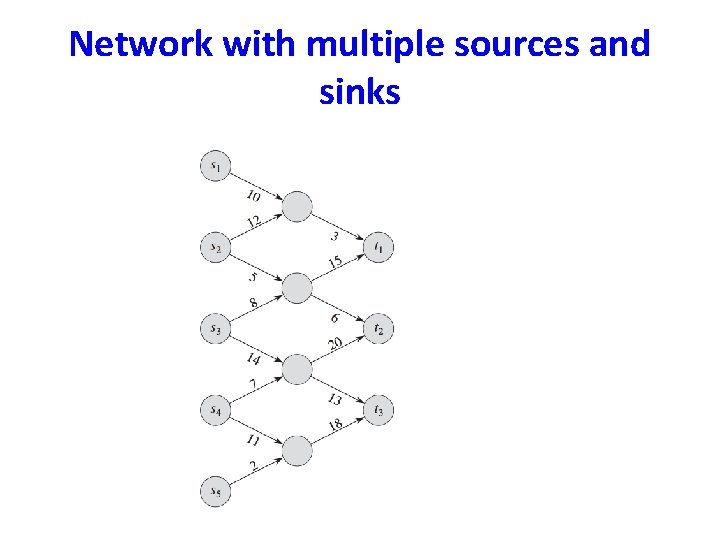
Network with multiple sources and sinks

Max Flow Network • We can reduce the problem of determining a maximum flow in a network with multiple sources and multiple sinks to an ordinary maximum-flow problem.
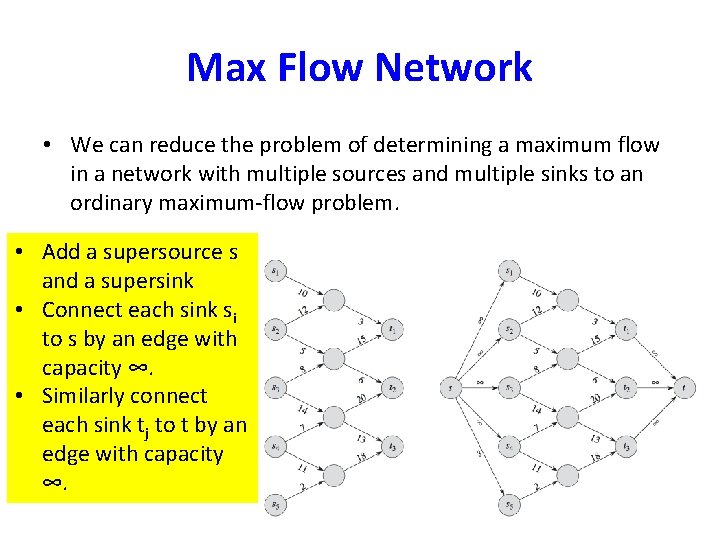
Max Flow Network • We can reduce the problem of determining a maximum flow in a network with multiple sources and multiple sinks to an ordinary maximum-flow problem. • Add a supersource s and a supersink • Connect each sink si to s by an edge with capacity ∞. • Similarly connect each sink tj to t by an edge with capacity ∞.

Ford-Fulkerson Method • Iteratively increases the value of the flow. • Start with f(e) = 0 for all e, giving an initial flow of value 0. • The flow is increased in G by finding an “augmenting path” in an associated “residual network” Gf. • Increase flow in G can then be pushed along the edges of the augmenting path.

Residual Networks • Flow network G=(V, E) with source node s and sink node t. • Let f be a flow in G. • Define the residual capacity cf(u, v) by – cf(u, v) = c(u, v) –f(u, v) – cf(v, u) = f(u, v) if f(u, v) > 0 • We assume that if (u, v) is an element of E, (v, u) is not an element of E.
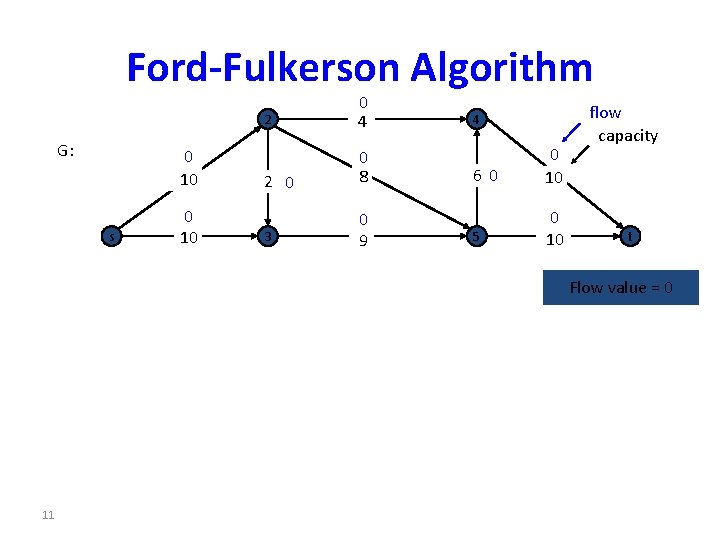
Ford-Fulkerson Algorithm G: 0 10 s 0 10 2 0 4 2 0 0 8 3 0 9 4 60 0 10 5 0 10 flow capacity t Flow value = 0 11
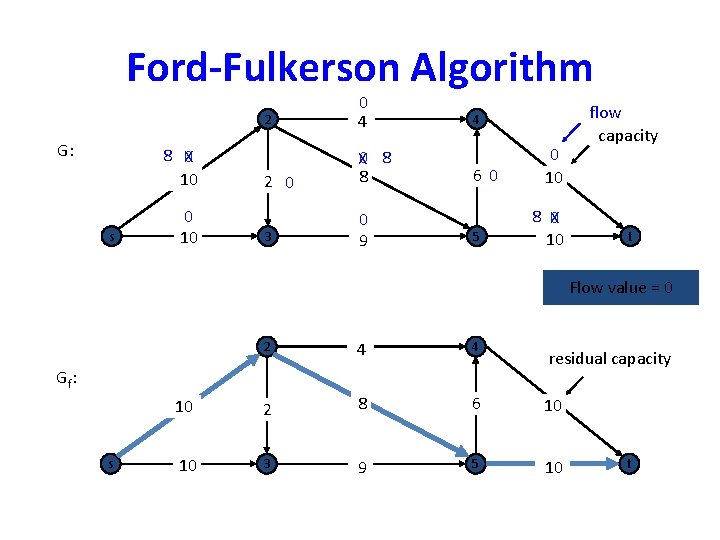
Ford-Fulkerson Algorithm G: 8 X 0 10 s 0 10 2 0 4 2 0 X 0 8 8 3 0 9 4 60 5 0 10 8 X 0 10 flow capacity t Flow value = 0 2 4 4 2 8 6 10 3 9 5 10 Gf: 10 s 10 residual capacity t
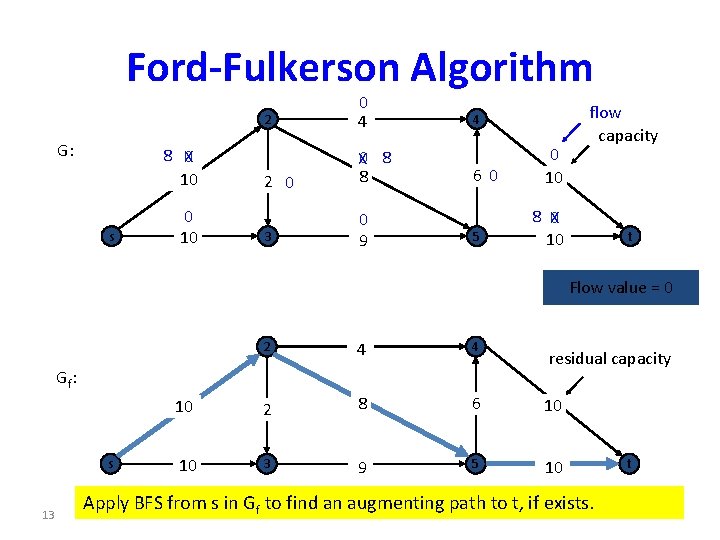
Ford-Fulkerson Algorithm G: 8 X 0 10 s 0 10 2 0 4 2 0 X 0 8 8 3 0 9 4 60 5 0 10 flow capacity 8 X 0 10 t Flow value = 0 2 4 4 2 8 6 10 3 9 5 10 Gf: 10 s 13 10 residual capacity Apply BFS from s in Gf to find an augmenting path to t, if exists. t
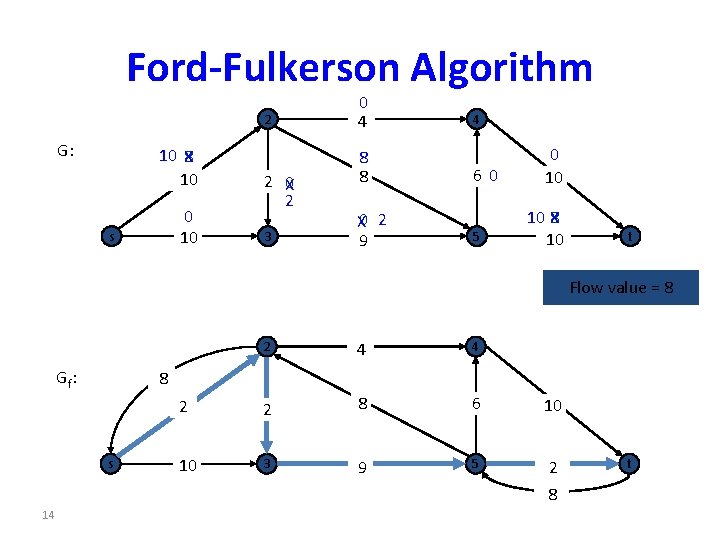
Ford-Fulkerson Algorithm 2 G: 10 X 8 10 0 10 s 2 X 0 2 3 0 4 8 8 X 0 2 9 4 60 5 0 10 8 10 X 10 t Flow value = 8 Gf: 4 4 2 2 8 6 10 10 3 9 5 2 8 8 s 14 2 t
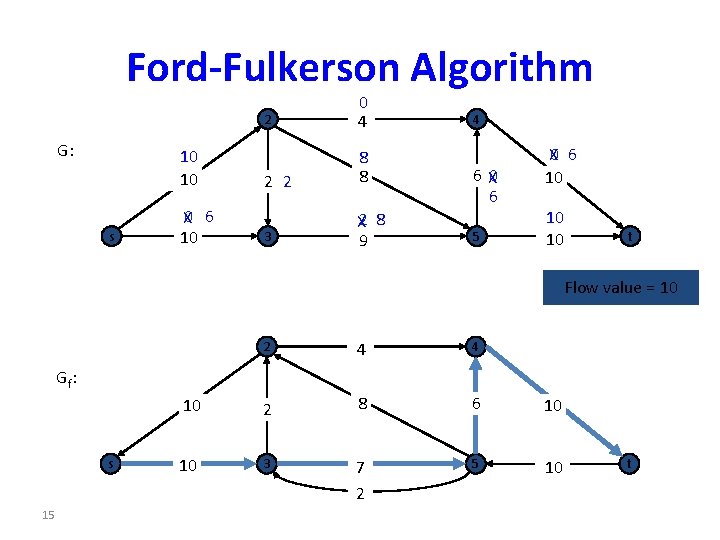
Ford-Fulkerson Algorithm G: 10 10 s X 0 6 10 2 0 4 2 2 8 8 3 X 2 8 9 4 6 X 0 6 5 X 0 6 10 10 10 t Flow value = 10 2 4 4 10 2 8 6 10 10 3 7 2 5 10 Gf: s 15 t
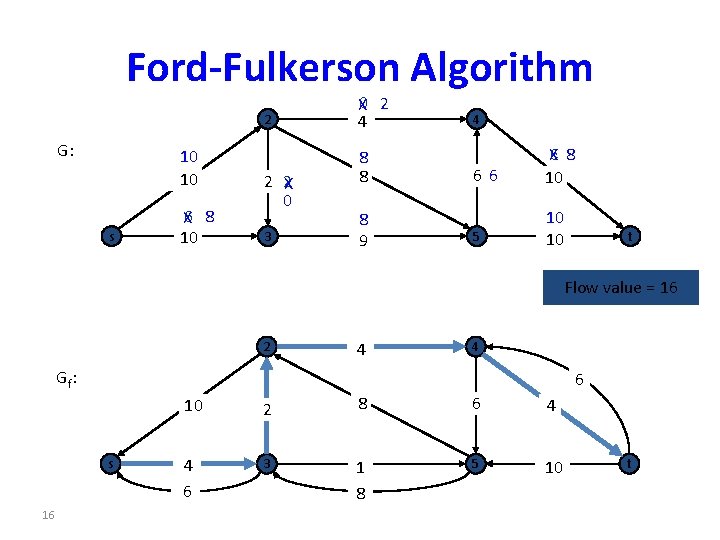
Ford-Fulkerson Algorithm 2 G: 10 10 s X 6 8 10 2 2 X 0 3 X 0 2 4 8 8 8 9 4 66 X 6 8 10 5 10 10 t Flow value = 16 2 4 Gf: 6 s 16 4 10 2 8 6 4 4 6 3 1 8 5 10 t
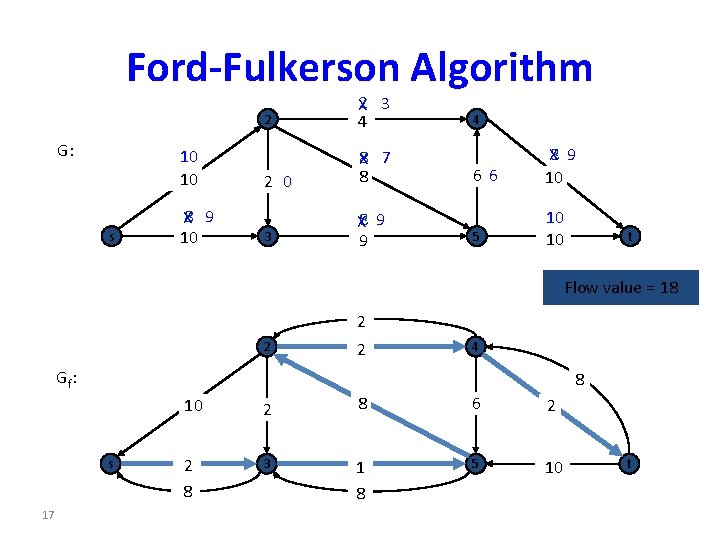
Ford-Fulkerson Algorithm G: 10 10 s X 8 9 10 2 X 2 3 4 2 0 8 7 X 8 3 X 8 9 9 4 66 X 8 9 10 5 10 10 t Flow value = 18 2 2 2 Gf: 8 s 17 4 10 2 8 6 2 2 8 3 1 8 5 10 t
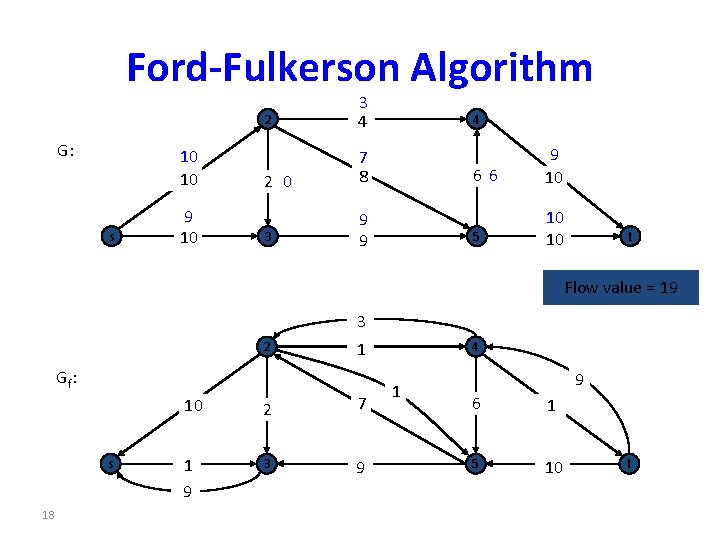
Ford-Fulkerson Algorithm G: 10 10 s 9 10 2 3 4 2 0 7 8 3 9 9 4 66 9 10 5 10 10 t Flow value = 19 3 2 1 Gf: s 18 10 2 7 1 9 3 9 4 1 9 6 1 5 10 t
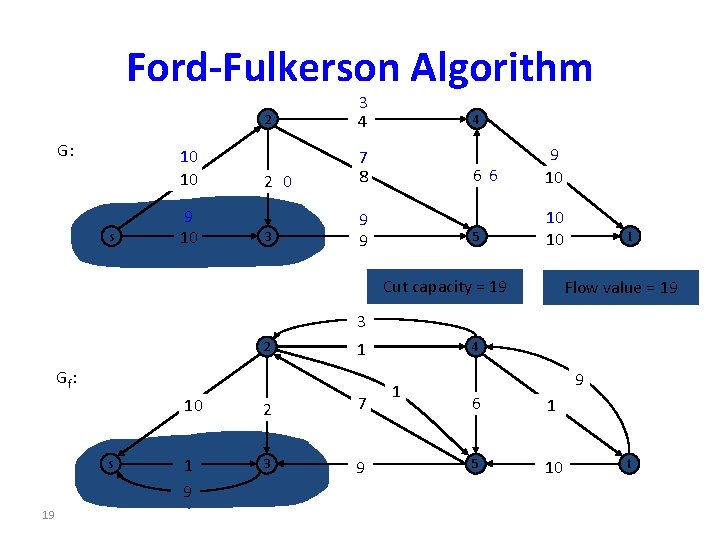
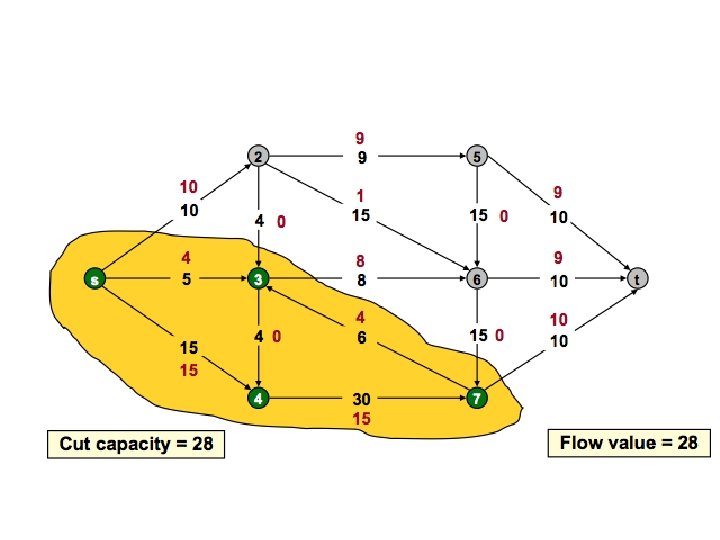
Ford-Fulkerson Algorithm G: 10 10 s 9 10 2 3 4 2 0 7 8 3 9 9 4 66 9 10 5 10 10 Cut capacity = 19 t Flow value = 19 3 2 1 Gf: s 19 10 2 7 1 9 3 9 4 1 9 6 1 5 10 t

Ford-Fulkerson Method

Residual Networks • Flow network G=(V, E) with source node s and sink node t. • Let f be a flow in G. • Define the residual capacity cf(u, v) by – cf(u, v) = c(u, v) –f(u, v) – cf(v, u) = f(u, v) if f(u, v) > 0 • We assume that if (u, v) is an element of E, (v, u) is not an element of E.

Ford-Fulkerson Method

Cuts in the Flow Network • How do we know that when the algorithm terminates, we have found a maximum flow? • Max-flow min-cut theorem is very famous.

Cuts in the Flow Network • A cut (S, T) of flow network G=(V, E) is a partition of V into S and T=V-S such that s ε S and t ε T. • net flow f(S, T)is defined as follows:

Cuts in the Flow Network • A cut (S, T) of flow network G=(V, E) is a partition of V into S and T=V-S such that s ε S and t ε T. • net flow f(S, T)is defined as follows: f(S, T) = 19

Cuts in the Flow Network • A cut (S, T) of flow network G=(V, E) is a partition of V into S and T=V-S such that s ε S and t ε T. • net flow f(S, T)is defined as follows: • The capacity of the cut (S, T) is
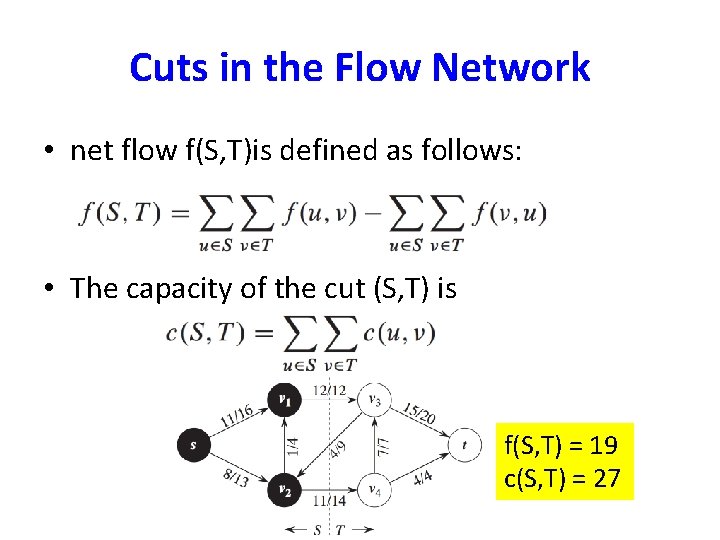
Cuts in the Flow Network • net flow f(S, T)is defined as follows: • The capacity of the cut (S, T) is f(S, T) = 19 c(S, T) = 27
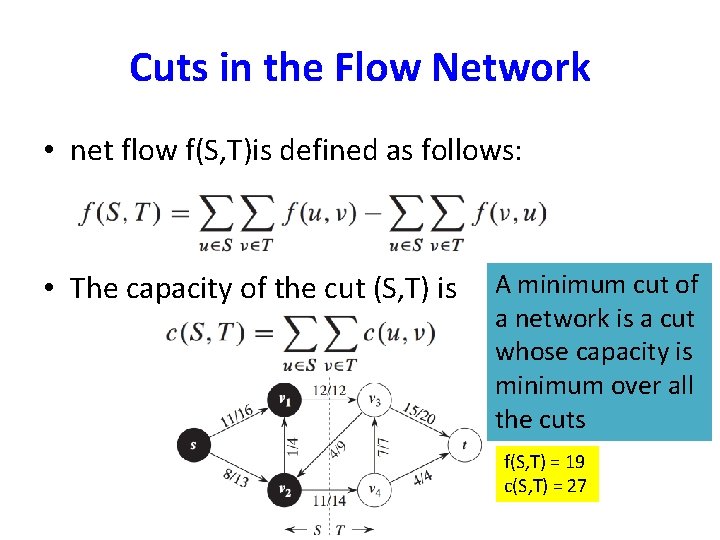
Cuts in the Flow Network • net flow f(S, T)is defined as follows: • The capacity of the cut (S, T) is A minimum cut of a network is a cut whose capacity is minimum over all the cuts f(S, T) = 19 c(S, T) = 27

Max-flow Min-cut Theorem
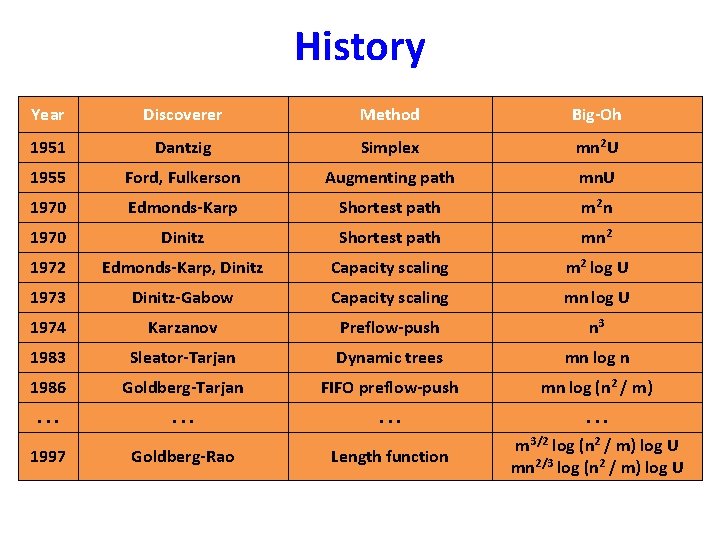
History Year Discoverer Method Big-Oh 1951 Dantzig Simplex mn 2 U 1955 Ford, Fulkerson Augmenting path mn. U 1970 Edmonds-Karp Shortest path m 2 n 1970 Dinitz Shortest path mn 2 1972 Edmonds-Karp, Dinitz Capacity scaling m 2 log U 1973 Dinitz-Gabow Capacity scaling mn log U 1974 Karzanov Preflow-push n 3 1983 Sleator-Tarjan Dynamic trees mn log n 1986 Goldberg-Tarjan FIFO preflow-push mn log (n 2 / m) . . . Length function m 3/2 log (n 2 / m) log U mn 2/3 log (n 2 / m) log U 1997 Goldberg-Rao

Applications of Flow Network • Find the min-cut of G =(V, E) separating two given nodes u and v. – Treat u as the source node and v as sink node. – Set the capacity of each edge to be 1. – Solve the max-flow problem in G. – Size of min-cut separting u and v is |f| where f is the maximum flow.

Edge Connectivity of an Undirected Graphs • The edge connectivity of an undirected graph is the minimum number k of edges that must be removed to disconnect the graph.

Edge Connectivity of an Undirected Graphs • The edge connectivity of an undirected graph is the minimum number k of edges that must be removed to disconnect the graph.

Maximum Bipartite Matching • A matching of an undirected graph G = (V, E) is a subset of edges M of E such that for all vertices v of V, at most one edge of M is incident on v. • A maximum matching is a matching of maximum cardinality. • An undirected graph G = (V, E) is a bipartite graph if V can be partitioned into L and R such that for every (u, v) of E, u ε L and v ε R.
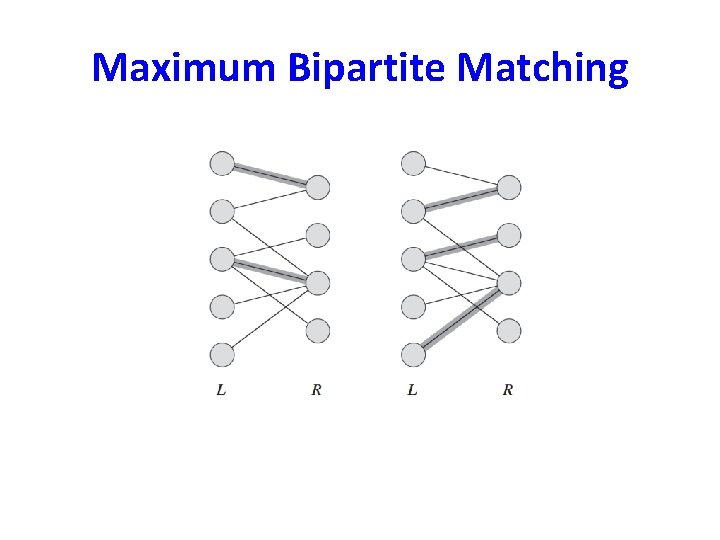
Maximum Bipartite Matching

Maximum Bipartite Matching • Corresponding Flow Network. – We let the source s and sink t be new vertices not in V, and we let V’ = V U {s, t}. – E’ = {(s, u) : u ε L} U {(v, t) : v ε R} U {(u, v) : (u, v) ε E}. – Assign unit capacity to each edge. – The maximum flow in G’ = (V’, E’) realizes the maximum matching.
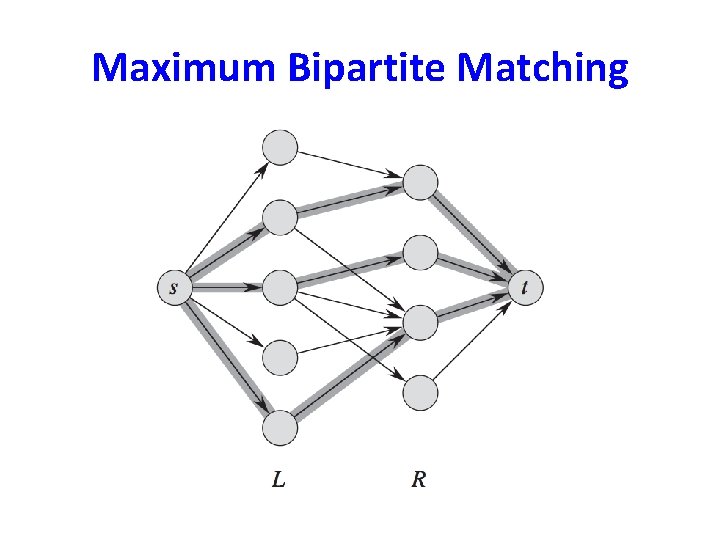
Maximum Bipartite Matching

maximum edge-disjoint paths between s and t • Corresponding Flow Network. – Source s and sink t are elements of V. – G=(V, E) is our graph – Assign unit capacity to each edge. – The maximum flow in G = (V, E) realizes the maximum edge-disjoint paths.

Escape Problem (Corman et. al page 760) • Given n x n grid. • m starting points (x 1, y 1), …, (xm, ym) are given. • Determine whethere are m vertex disjoint paths from the starting points to any m different points on the boundary.
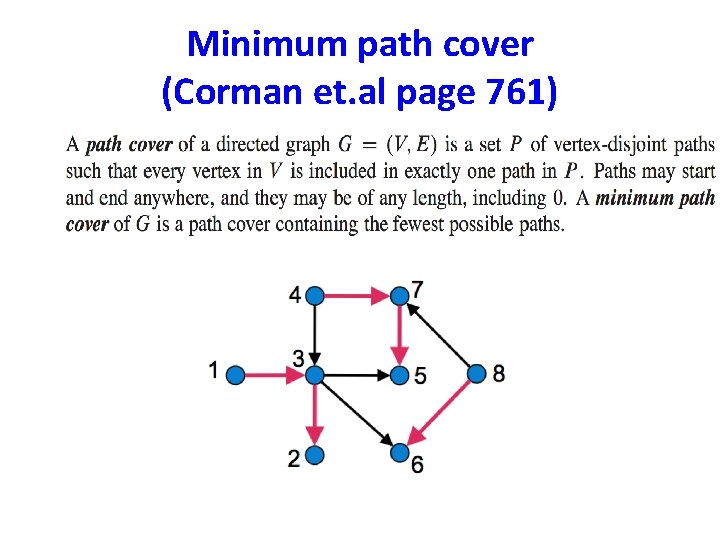
Minimum path cover (Corman et. al page 761)
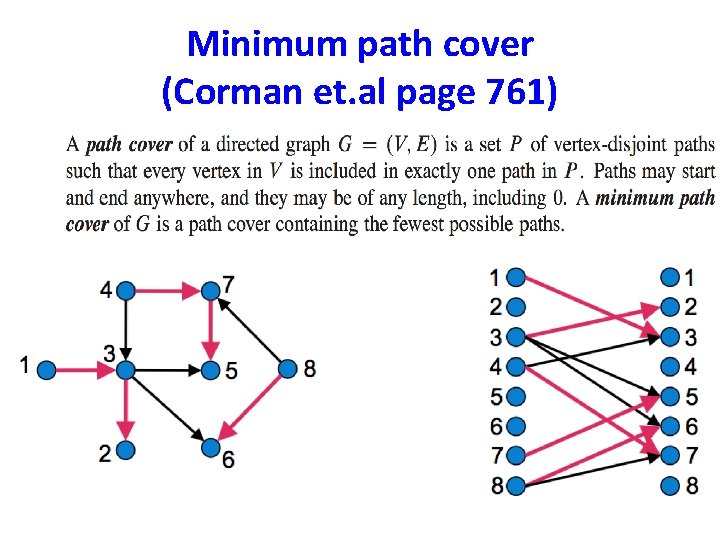
Minimum path cover (Corman et. al page 761)

Minimum path cover (Corman et. al page 761)


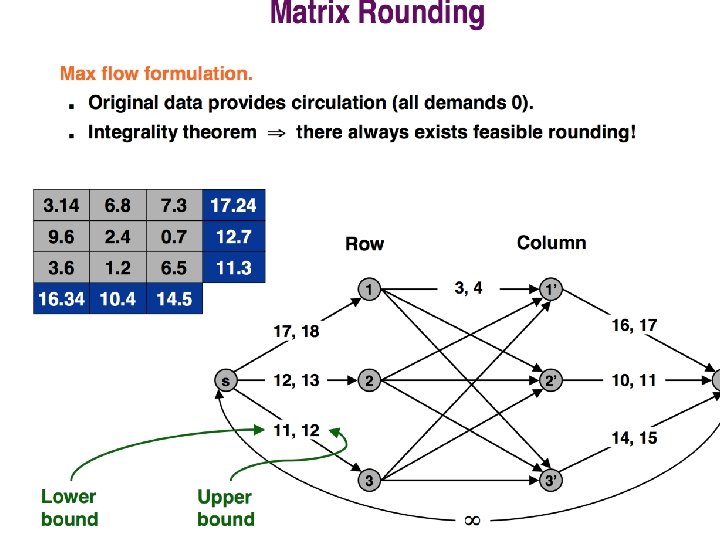
- Slides: 46