Maximum Flow Networks Hiren Patel Ujjval Patel CONTENTS








![• Procedure Ford_Fulkerson_method(G, s, t): For each edge (u, v) ∈ E[G] do • Procedure Ford_Fulkerson_method(G, s, t): For each edge (u, v) ∈ E[G] do](https://slidetodoc.com/presentation_image_h2/e91de99ccbd0cf3b63ff049118a24c4a/image-11.jpg)










- Slides: 26

Maximum Flow Networks -Hiren Patel -Ujjval Patel

CONTENTS • Network flows on directed acyclic graphs • Ford-fulkerson Algorithms -Residual networks • Min cut Max flow theorem • Enmond kalp algorithm • Max Bipartite matching

Network flows on directed acyclic graphs • • DAG is a directed graph with no cycles. Flow network: a flow network G = (V, E) is a directed graph in which each edge (u, v) ∈ E has a nonnegative capacity c(u, v) >= 0. if (u, v) ∉ E , we assume that c(u, v) = 0. We distinguish two vertices in flow network , source s and sink t. • The source produces the material at a steady rate. • The sink consumes the material at a steady rat Objective : how much of material can be imposed through network can handle network that

• Flow: A flow in G is a real-valued function f : V × V → R that satisfies three properties: • 1. Capacity constraint : For all u, v ∈ V, we require f(u, v) ≤ c(u, v). • The net flow from one vertex to another must not exceed the given capacity. • 2. Skew symmetry : For all u, v ∈ V, we require f(u, v) = f(v, u). • The net flow from a vertex u to a vertex v is the negative of the net flow in the • 3. Flow conservation : For all u ∑ f(u, v) = 0. ∈ V - {s, t}, we require v∈V The quantity f(u, v), which can be positive or negative , is called the net flow from vertex u to v. The value of the flow is defined as | f | = ∑ f(s, v) that is the totat net Flow out of the source. v∈V

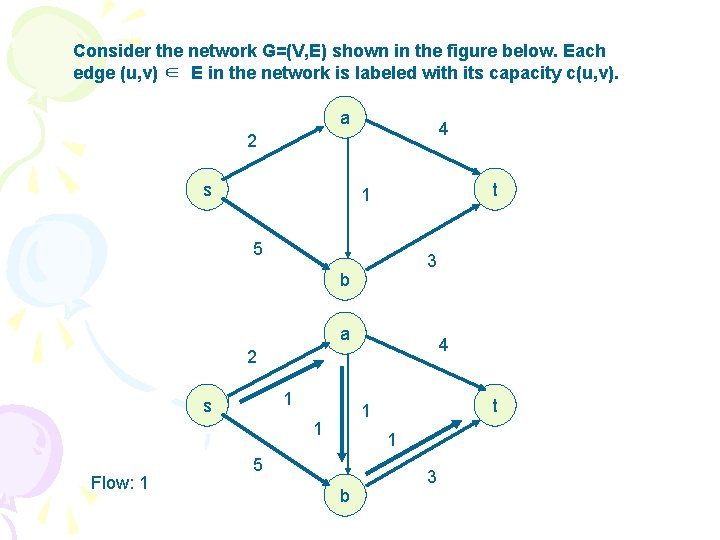
Consider the network G=(V, E) shown in the figure below. Each edge (u, v) ∈ E in the network is labeled with its capacity c(u, v). a 4 2 s t 1 5 3 b a 4 2 1 s 1 Flow: 1 t 1 1 5 b 3

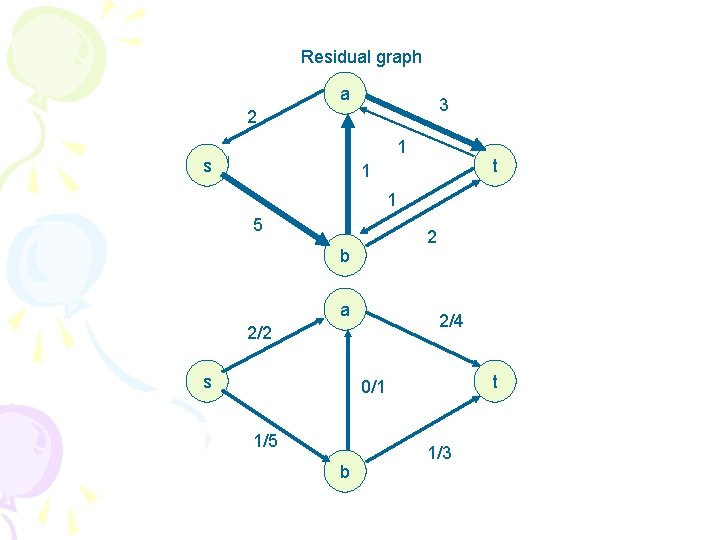
Residual graph a 4 1 1 s t 1 1 5 2 b a 1/4 2/2 s t 1/1 5 b 1/3

Residual graph a 3 2 1 s t 1 1 5 2 b a 2/4 2/2 s t 0/1 1/5 b 1/3

a 2 2 2 1 s 1 t 1 4 2 b a 2/2 2/4 1 s 3/5 t 3/3 b

a 2 2 2 s t 1 2 3 3 b Max Flow : 5

Ford fulkerson algorithm • The Ford_Fulkerson method is iterative, • Starts with f(u, v) for (u, v) ∈ V, initial flow of value 0. • The method is based on the augmenting path which is • defined as a path from s to t along which we can push • more flow and then augment flow along this path.
![Procedure FordFulkersonmethodG s t For each edge u v EG do • Procedure Ford_Fulkerson_method(G, s, t): For each edge (u, v) ∈ E[G] do](https://slidetodoc.com/presentation_image_h2/e91de99ccbd0cf3b63ff049118a24c4a/image-11.jpg)
• Procedure Ford_Fulkerson_method(G, s, t): For each edge (u, v) ∈ E[G] do f[u, v] 0 f[v, u] 0 While there exists a path p from s to t in the residual network G 1 do c 1(p) min{ c 1(u, v): (u, v) is in p} for each edge (u, v) in p do f[u, v] + c 1(p) f[u, v] -f[u, v]

• Running time for this algorithms is O(E * |f*|) where f* is the maximum flow found by algorithm. • First three Lines take time θ(E). • The while loop of last five lines is executed at most |f*| times, since the flow value increases by at least one unit in each iteration.

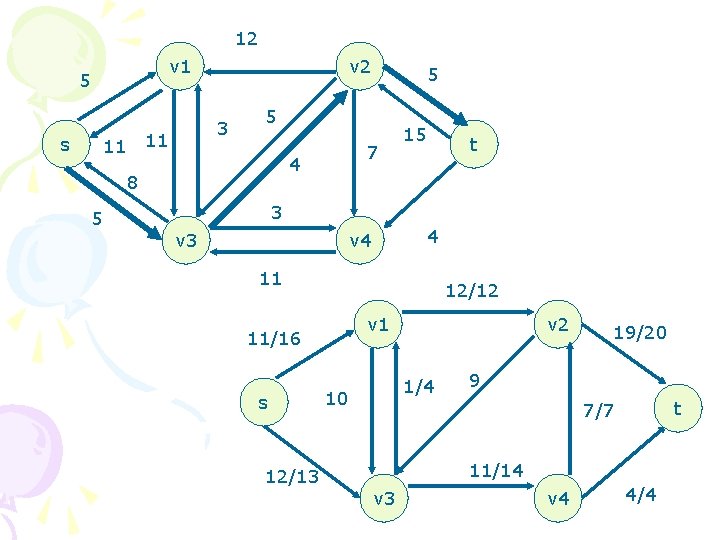
Example: 12 v 1 16 s 13 v 2 4 10 20 9 t 7 14 v 3 4 v 4 4/12 v 1 4/16 s 13 v 2 4 10 20 4/9 t 7 4/14 v 3 v 4 4/4

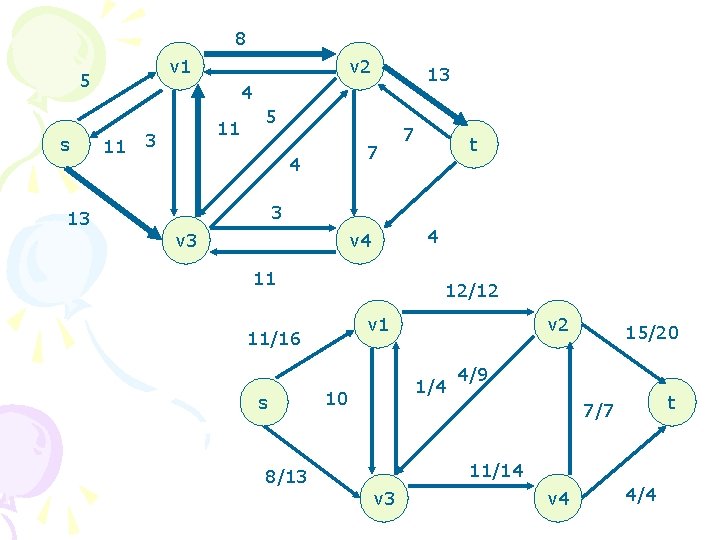
8 v 1 12 s 13 v 2 20 4 4 5 4 10 t 7 4 10 v 3 4 v 4 4 4/12 11/16 s 13 v 1 v 2 4 7/10 7/20 4/9 t 7/7 11/14 v 3 v 4 4/4

8 v 1 5 s 13 v 2 13 4 11 11 3 5 7 4 7 t 3 v 3 4 v 4 11 12/12 v 1 11/16 s 8/13 v 2 1/4 10 15/20 4/9 t 7/7 11/14 v 3 v 4 4/4

12 v 1 5 s 3 11 11 v 2 5 7 4 8 5 5 15 t 3 v 3 4 v 4 11 12/12 v 1 11/16 s 12/13 v 2 1/4 10 19/20 9 t 7/7 11/14 v 3 v 4 4/4

12 v 1 5 3 11 11 s v 2 9 7 1 19 12 1 3 v 4 11 4 t

Cut of flow netwoks • Cut : a cut (S, T) of flow network G = (V, E) is a partition of V into S and T = V-S such that s ∈ S and t ∈ T. If f is a flow then net flow across the cut (S, T) is defined to be f(S, T). The capacity of the cut (S, T) is c(S, T).

Max flow min cut theorem • The ford fulkerson method repeatedly augments the flow along the augmenting paths until the a max. flow has been found. • This theorem tell us that a flow is max. if and only if its residual network contains no augmenting path.

Theorem states that , If f is a flow in a flow network, G = (V, E) with the source s and sink t then The following conditions are equivalent: 1. F is a max. flow in G. 2. The residual network G 1 contains no augments paths. 3. |F| = c(S, T) for some cut (S, T) of G.

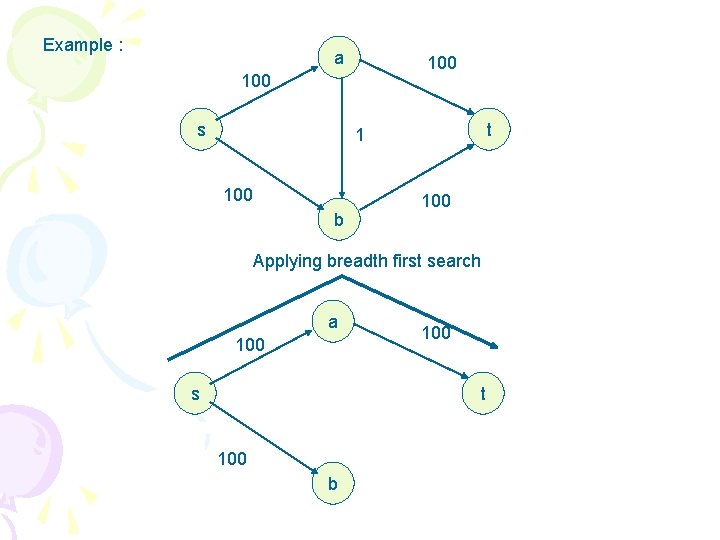
Edmond karp algorithm • The bound on Ford fulkerson can be improved if we implement the computation of the augmenting path p with a breadth first search, that is , if the augmenting path is a shortest path from s to t in the residual network, where each edge has unit distance (weight). we call ford fulkerson method so implemented the Edmonds-Karp algorithm runs in O(V*E*E).

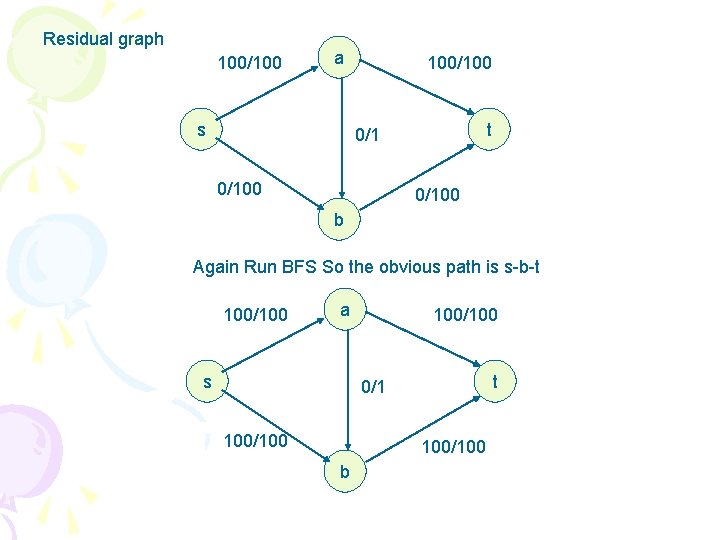
Example : a 100 s t 1 100 b 100 Applying breadth first search a 100 s 100 t 100 b

Residual graph 100/100 a s 100/100 t 0/100 b Again Run BFS So the obvious path is s-b-t 100/100 a s 100/100 t 0/1 100/100 b

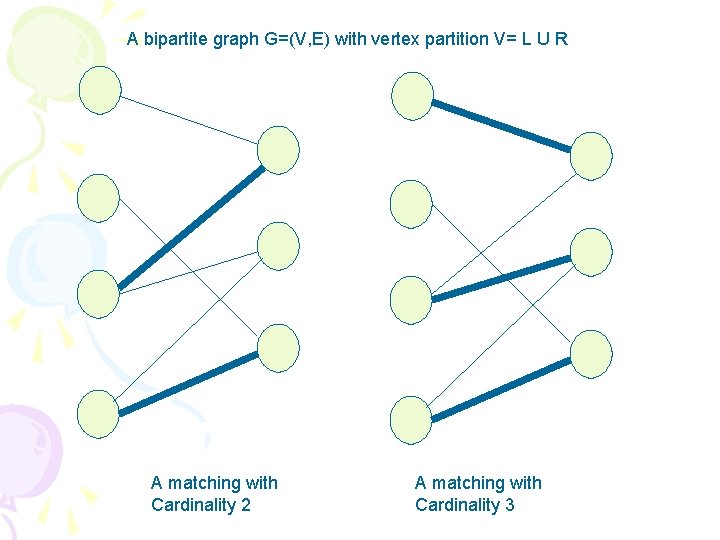
Maximum Bipartite Matching • Given an undirected graph G=(V, E), maching is a subset of edges M is subset of E such that for all vertices v ∈ V, at most one edge of M is incident on v. We say that a vertex v ∈V is matched by matching M if some edge in M is incident on v; otherwise, v id unmatched. A maximum matching is a matching of maximum cardinality, that is, a matching M such that for any matchimng M’, we have |M|>= |M’|.

A bipartite graph G=(V, E) with vertex partition V= L U R A matching with Cardinality 2 A matching with Cardinality 3

• We can solve the maximum match finding problem using flow networks. • Put source and sink on the graph such that source connects all the vertices on left side of the graph with single edge to each vertex and do the same for the sink. Now assign weight 1 to all the edges in the graph. • Run ford fulkerson algorithm to find max flow. • Max. cardinality = Max flow
 Ujjval patel
Ujjval patel Local max
Local max Maximum parsimony vs maximum likelihood
Maximum parsimony vs maximum likelihood Maximum likelihood vs maximum parsimony
Maximum likelihood vs maximum parsimony Hiren international mumbai office
Hiren international mumbai office Dr hiren joshi
Dr hiren joshi Difference between virtual and datagram circuit
Difference between virtual and datagram circuit Backbone networks in computer networks
Backbone networks in computer networks Baseball elimination problem maximum flow
Baseball elimination problem maximum flow Hedera: dynamic flow scheduling for data center networks
Hedera: dynamic flow scheduling for data center networks Fio2 calculation nasal cannula
Fio2 calculation nasal cannula T piece
T piece Trach collar oxygen flow rates
Trach collar oxygen flow rates Lumina flow
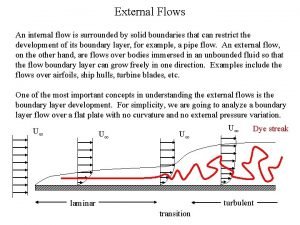
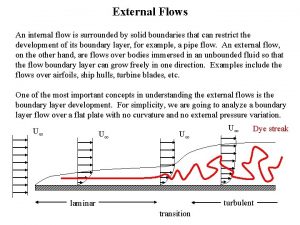
Lumina flow Internal and external flow
Internal and external flow Energy naturally flows from warmer matter to cooler matter.
Energy naturally flows from warmer matter to cooler matter. Oikos meaning
Oikos meaning Transform flow and transaction flow
Transform flow and transaction flow Transform flow and transaction flow
Transform flow and transaction flow Definition
Definition Internal vs external flow
Internal vs external flow Data flow vs control flow
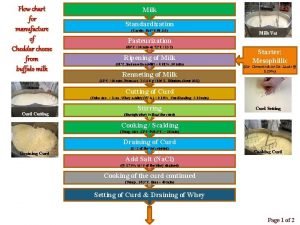
Data flow vs control flow Cheese production process flow chart
Cheese production process flow chart Control flow and data flow computers
Control flow and data flow computers Transaction flow graph
Transaction flow graph Dr vikas patel
Dr vikas patel Dr vikas patel
Dr vikas patel