Maximum Flow c v 46 11 33 s

Maximum Flow c v 4/6 1/1 3/3 s 3/5 Maximum Flow w 1/1 u 9/29/2020 6: 44 PM 3/3 2/2 t 4/7 1/9 3/5 z 1

Outline and Reading Flow networks n n Flow (§ 8. 1. 1) Cut (§ 8. 1. 2) Maximum flow n n Augmenting path (§ 8. 2. 1) Maximum flow and minimum cut (§ 8. 2. 1) Ford-Fulkerson’s algorithm (§ 8. 2. 2 -8. 2. 3) Edmonds-Karp algorithm (§ 8. 2. 4) Maximum Bipartite Matching Minimum Cost Flow (§ 8. 4) 9/29/2020 6: 44 PM Maximum Flow 2

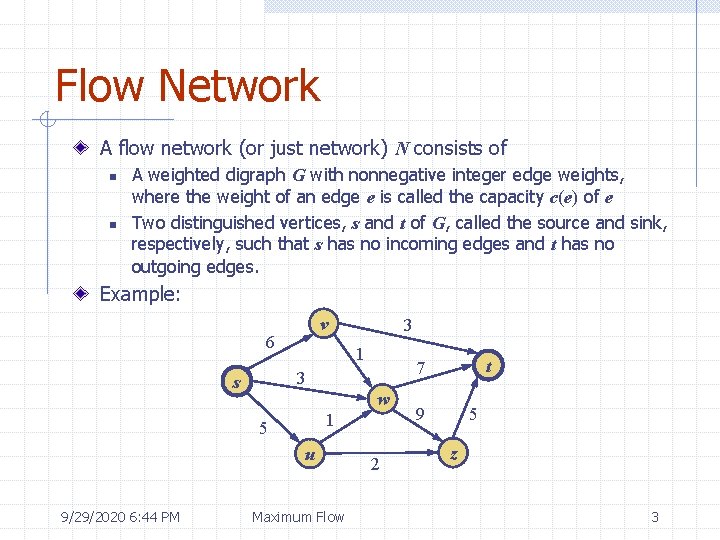
Flow Network A flow network (or just network) N consists of n n A weighted digraph G with nonnegative integer edge weights, where the weight of an edge e is called the capacity c(e) of e Two distinguished vertices, s and t of G, called the source and sink, respectively, such that s has no incoming edges and t has no outgoing edges. Example: v 6 1 w 1 5 u Maximum Flow t 7 3 s 9/29/2020 6: 44 PM 3 2 9 5 z 3

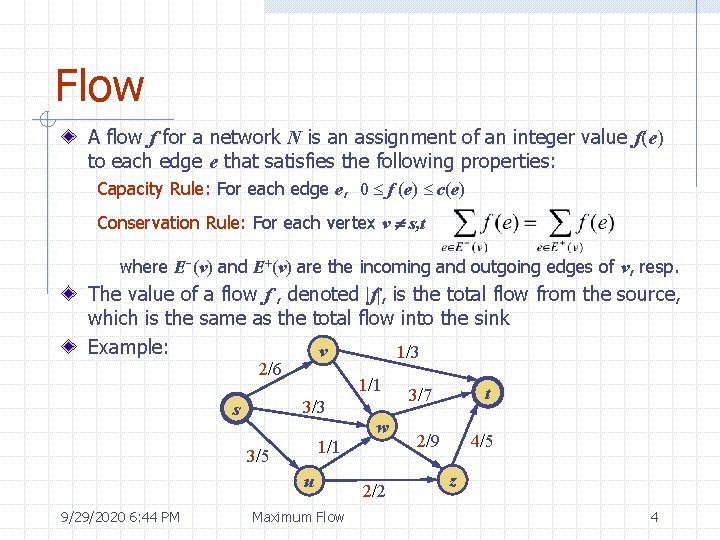
Flow A flow f for a network N is an assignment of an integer value f(e) to each edge e that satisfies the following properties: Capacity Rule: For each edge e, 0 f (e) c(e) Conservation Rule: For each vertex v s, t where E-(v) and E+(v) are the incoming and outgoing edges of v, resp. The value of a flow f , denoted |f|, is the total flow from the source, which is the same as the total flow into the sink Example: v 1/3 2/6 1/1 3/3 s 1/1 3/5 u 9/29/2020 6: 44 PM w Maximum Flow 2/2 t 3/7 2/9 4/5 z 4

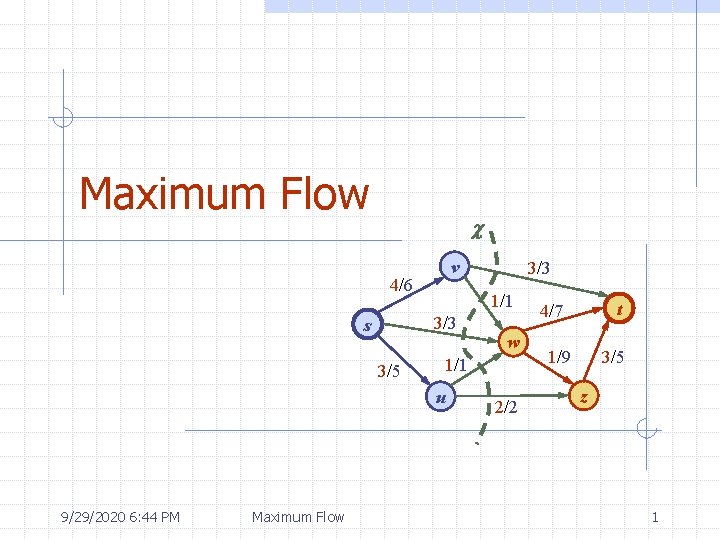
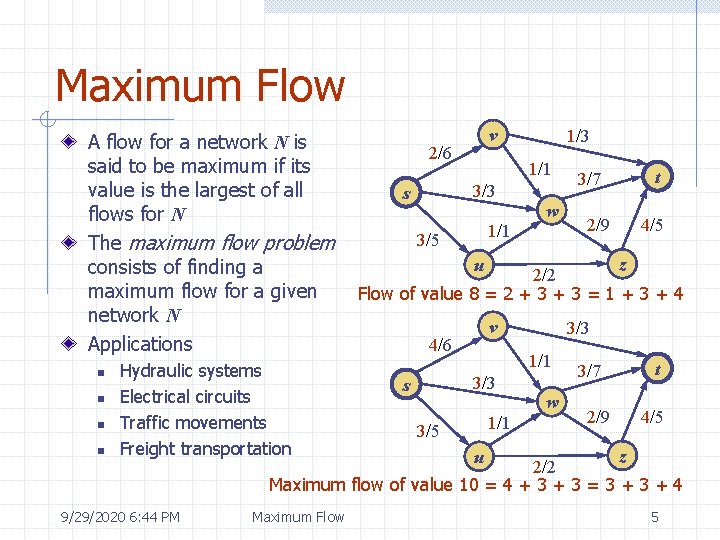
Maximum Flow A flow for a network N is said to be maximum if its value is the largest of all flows for N The maximum flow problem consists of finding a maximum flow for a given network N Applications n n Hydraulic systems Electrical circuits Traffic movements Freight transportation 9/29/2020 6: 44 PM v 2/6 1/1 3/3 s 1/3 w 1/1 3/5 3/7 2/9 t 4/5 z 2/2 Flow of value 8 = 2 + 3 = 1 + 3 + 4 u v 4/6 1/1 3/3 s 3/3 1/1 3/5 w 3/7 2/9 t 4/5 z 2/2 Maximum flow of value 10 = 4 + 3 = 3 + 4 Maximum Flow u 5

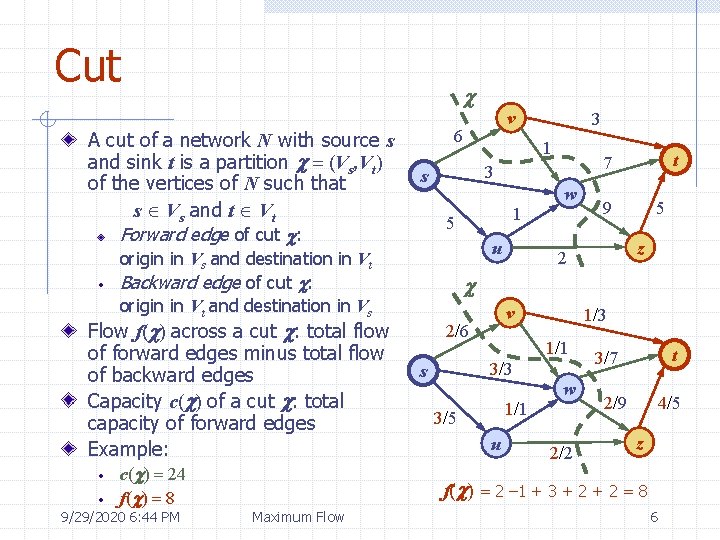
Cut c A cut of a network N with source s and sink t is a partition c = (Vs, Vt) of the vertices of N such that s Vs and t Vt Forward edge of cut c: 6 9/29/2020 6: 44 PM Maximum Flow 3 1 s w 1 5 u t 7 3 origin in Vs and destination in Vt Backward edge of cut c: origin in Vt and destination in Vs Flow f(c) across a cut c: total flow of forward edges minus total flow of backward edges Capacity c(c) of a cut c: total capacity of forward edges Example: c(c) = 24 f(c) = 8 v 9 5 z 2 c v 2/6 1/1 3/3 s 1/3 w 1/1 3/5 u 2/2 t 3/7 2/9 4/5 z f(c) = 2 – 1 + 3 + 2 = 8 6

Flow and Cut Lemma: The flow f(c) across any cut c is equal to the flow value |f| Lemma: The flow f(c) across a cut c is less than or equal to the capacity c(c) of the cut Theorem: The value of any flow is less than or equal to the capacity of any cut, i. e. , for any flow f and any cut c, we have |f| c(c) 9/29/2020 6: 45 PM Maximum Flow c 1 c 2 v 2/6 1/1 3/3 s 3/5 1/3 w 1/1 u 2/2 t 3/7 2/9 4/5 z |f| = 8 c(c 1) = 6 + 3 + 1 + 2 = 12 c(c 2) = 3 + 7 + 9 + 2 = 21 7

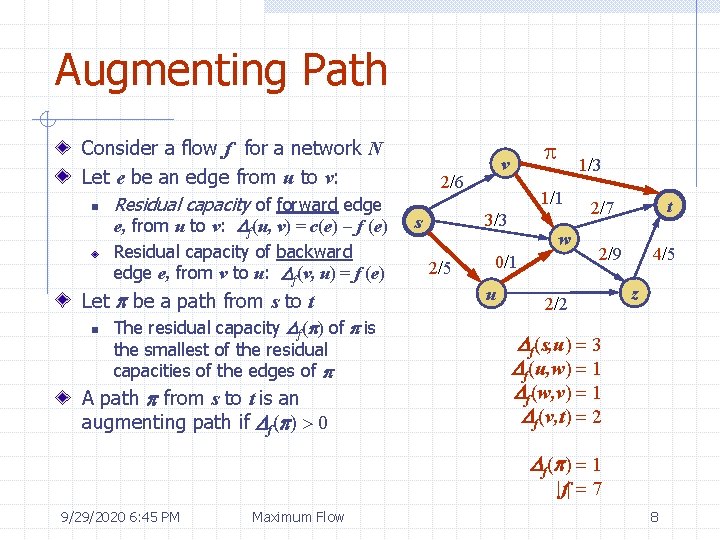
Augmenting Path Consider a flow f for a network N Let e be an edge from u to v: n Residual capacity of forward edge e, from u to v: Df(u, v) = c(e) - f (e) Residual capacity of backward edge e, from v to u: Df(v, u) = f (e) Let p be a path from s to t n The residual capacity Df(p) of p is the smallest of the residual capacities of the edges of p A path p from s to t is an augmenting path if Df(p) > 0 p v 2/6 1/1 3/3 s 2/5 1/3 w 0/1 u t 2/7 2/9 2/2 4/5 z Df(s, u) = 3 Df(u, w) = 1 Df(w, v) = 1 Df(v, t) = 2 Df(p) = 1 |f| = 7 9/29/2020 6: 45 PM Maximum Flow 8

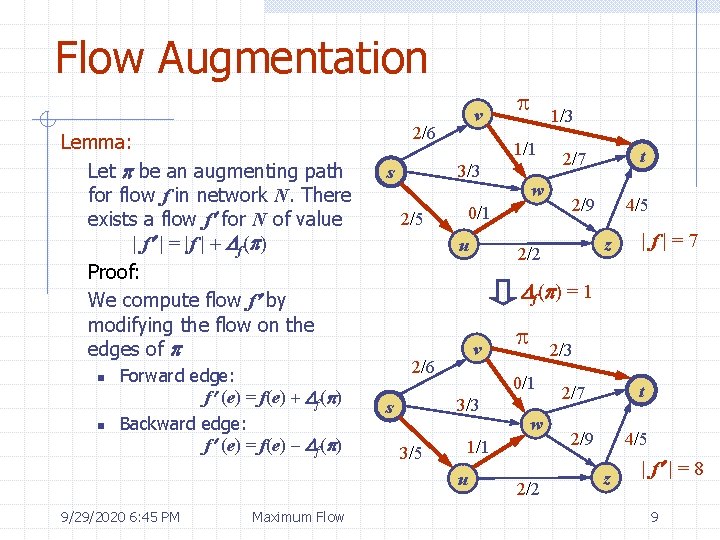
Flow Augmentation Lemma: Let p be an augmenting path for flow f in network N. There exists a flow f for N of value | f | = |f | + Df(p) Proof: We compute flow f by modifying the flow on the edges of p n n Forward edge: f (e) = f(e) + Df(p) Backward edge: f (e) = f(e) - Df(p) v 2/6 3/3 s 2/5 Maximum Flow 1/3 1/1 w 0/1 u t 2/7 2/9 4/5 z 2/2 |f|=7 Df(p) = 1 v 2/6 3/3 s 3/5 p 2/3 0/1 w 1/1 u 9/29/2020 6: 45 PM p 2/2 t 2/7 2/9 4/5 z | f | = 8 9

Ford-Fulkerson’s Algorithm Initially, f(e) = 0 for each edge e Repeatedly n n Search for an augmenting path p Augment by Df(p) the flow along the edges of p A specialization of DFS (or BFS) searches for an augmenting path An edge e is traversed from u to v provided Df(u, v) > 0 9/29/2020 6: 45 PM Algorithm Ford. Fulkerson. Max. Flow(N) for all e G. edges() set. Flow(e, 0) while G has an augmenting path p { compute residual capacity D of p } D for all edges e p { compute residual capacity d of e } if e is a forward edge of p d get. Capacity(e) - get. Flow(e) else { e is a backward edge } d get. Flow(e) if d < D D d { augment flow along p } for all edges e p if e is a forward edge of p set. Flow(e, get. Flow(e) + D) else { e is a backward edge } set. Flow(e, get. Flow(e) - D) Maximum Flow 10

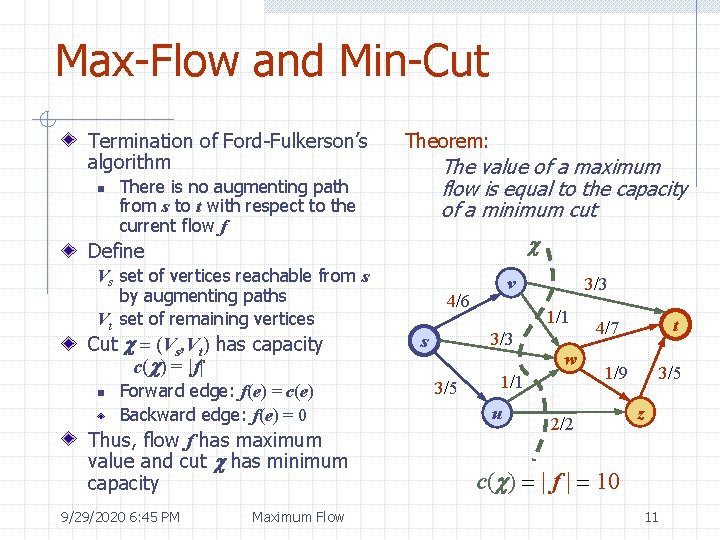
Max-Flow and Min-Cut Termination of Ford-Fulkerson’s algorithm n Theorem: The value of a maximum flow is equal to the capacity of a minimum cut There is no augmenting path from s to t with respect to the current flow f c Define Vs set of vertices reachable from s by augmenting paths Vt set of remaining vertices Cut c = (Vs, Vt) has capacity c(c) = |f| n Forward edge: f(e) = c(e) Backward edge: f(e) = 0 Thus, flow f has maximum value and cut c has minimum capacity 9/29/2020 6: 45 PM Maximum Flow v 4/6 1/1 3/3 s 3/5 3/3 w 1/1 u t 4/7 1/9 2/2 3/5 z c(c) = | f | = 10 11

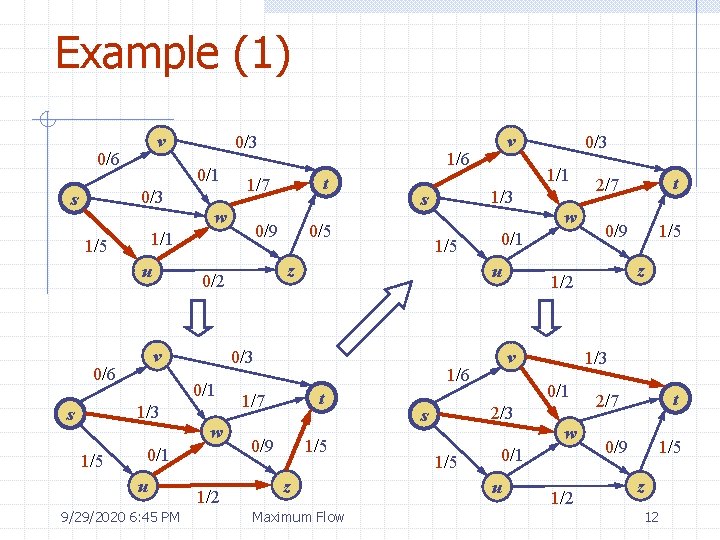
Example (1) v 0/6 0/1 0/3 s u w 0/1 u 9/29/2020 6: 45 PM 0/5 1/5 z u 1/2 t v 0/9 1/5 z Maximum Flow 1/5 0/9 1/5 z 1/3 0/1 w 0/1 u t 2/7 1/2 2/3 s w 0/1 1/6 1/7 0/3 1/1 1/3 s 0/3 0/1 1/3 t 0/9 0/2 v 0/6 1/5 w v 1/6 1/7 1/1 1/5 s 0/3 1/2 t 2/7 0/9 1/5 z 12

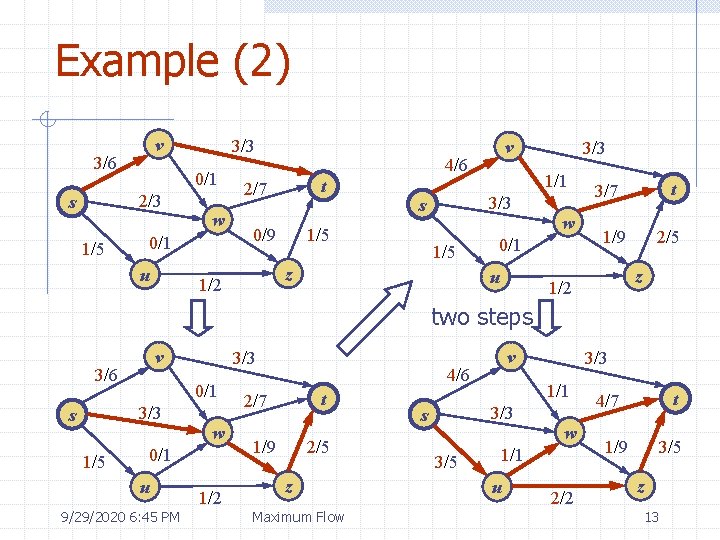
Example (2) v 3/6 0/1 2/3 s 1/5 3/3 w 0/1 u 4/6 t 2/7 0/9 1/5 3/3 1/1 3/3 s z 1/2 v w 0/1 u t 3/7 1/9 2/5 z 1/2 two steps v 3/6 0/1 3/3 s 1/5 3/3 w 0/1 u 9/29/2020 6: 45 PM 1/2 v 4/6 t 2/7 1/9 2/5 z Maximum Flow 1/1 3/3 s 3/5 3/3 w 1/1 u 2/2 t 4/7 1/9 3/5 z 13

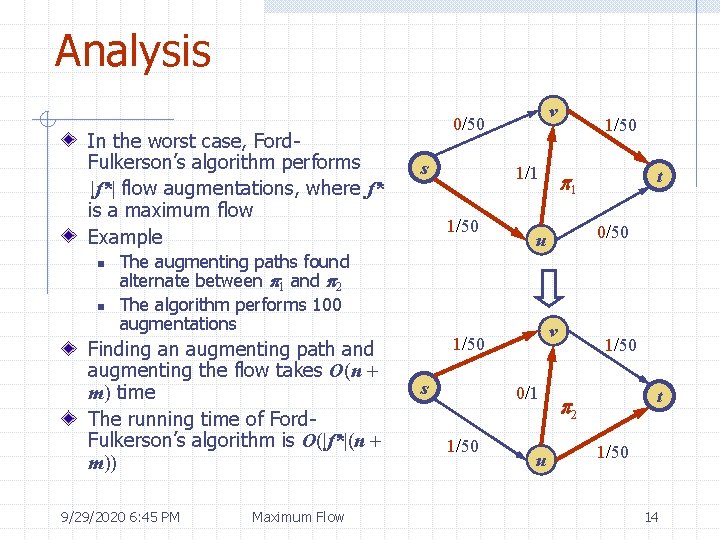
Analysis In the worst case, Ford. Fulkerson’s algorithm performs |f*| flow augmentations, where f* is a maximum flow Example n n s 1/1 1/50 The augmenting paths found alternate between p 1 and p 2 The algorithm performs 100 augmentations Finding an augmenting path and augmenting the flow takes O(n + m) time The running time of Ford. Fulkerson’s algorithm is O(|f*|(n + m)) 9/29/2020 6: 45 PM Maximum Flow v 0/50 1/50 0/50 v 0/1 u t p 1 u 1/50 s 1/50 t p 2 1/50 14

Edmonds-Karp Algorithm Variation of Ford-Fulkerson’s algorithm Uses a simple technique for finding good augmenting path in faster running time. n n n It is more greedy in the choice of path Chooses an augmenting path p with the smallest number of edges This can be done in O(m) by a modified BFS traversal Complexity O(n m 2) Lemma: The number of flow augmentations in the Edmonds-Karp algorithm for a network with n vertices and m edges is no more than n m. 9/29/2020 6: 45 PM Maximum Flow 15

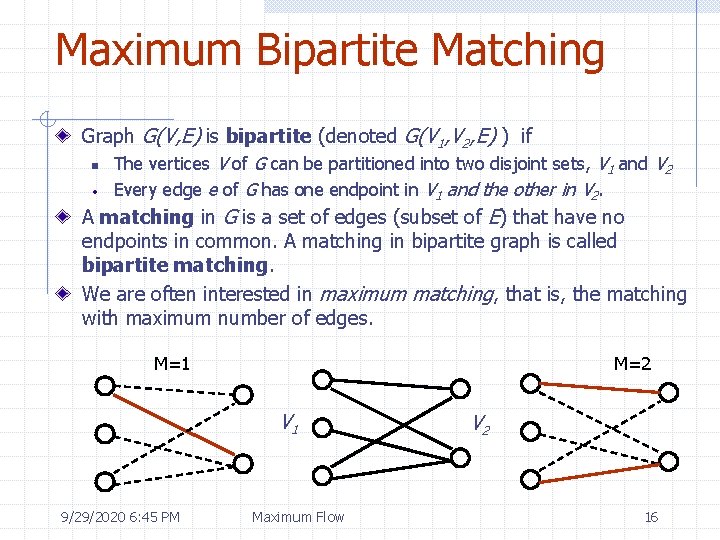
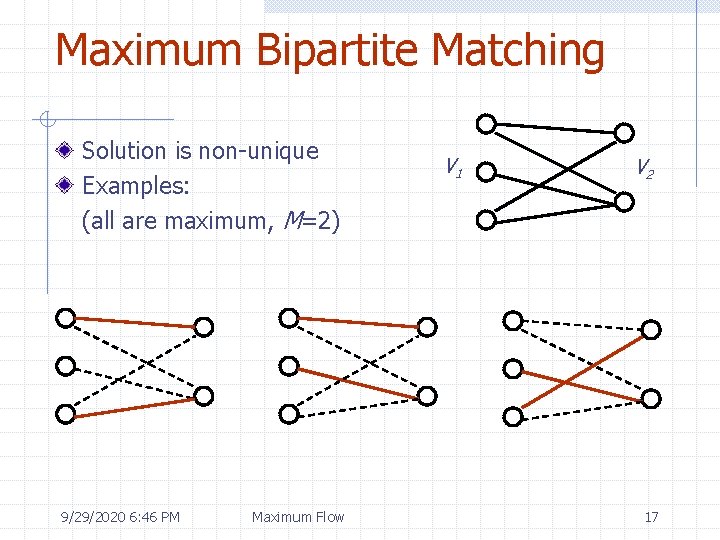
Maximum Bipartite Matching Graph G(V, E) is bipartite (denoted G(V 1, V 2, E) ) if n The vertices V of G can be partitioned into two disjoint sets, V 1 and V 2 Every edge e of G has one endpoint in V 1 and the other in V 2. A matching in G is a set of edges (subset of E) that have no endpoints in common. A matching in bipartite graph is called bipartite matching. We are often interested in maximum matching, that is, the matching with maximum number of edges. M=1 M=2 V 1 9/29/2020 6: 45 PM Maximum Flow V 2 16

Maximum Bipartite Matching Solution is non-unique Examples: (all are maximum, M=2) 9/29/2020 6: 46 PM Maximum Flow V 1 V 2 17

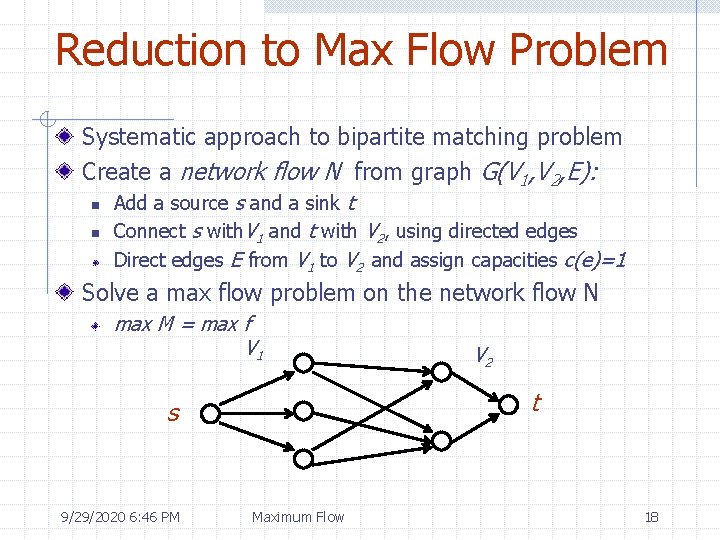
Reduction to Max Flow Problem Systematic approach to bipartite matching problem Create a network flow N from graph G(V 1, V 2, E): n n Add a source s and a sink t Connect s with. V 1 and t with V 2, using directed edges Direct edges E from V 1 to V 2 and assign capacities c(e)=1 Solve a max flow problem on the network flow N max M = max f V 1 t s 9/29/2020 6: 46 PM V 2 Maximum Flow 18

Reduction to Max Flow Problem Proof of correctness n n n f(e) = 1 e M Set M is a matching: w The flow through e is 0 or 1 (capacity is 1) w Each vertex in V 1 has exactly one incoming edge: by flow conservation rule there is at most one outgoing edge for v V 1 Each vertex in V 2 has exactly one outgoing edge: there is at most one incoming edge for v V 2 Hence, each vertex in V 1 will be paired in M by at most one vertex in V 2. , hence M is the matching. Finally, size of M = |f|. V 1 t s 9/29/2020 6: 46 PM V 2 Maximum Flow 19

Minimum Cost Flow Problem A variant of the max flow problem, applicable to networks where there is a cost w(e) associated with sending a unit flow through an edge. n Associate cost w(e) with each edge e in the network N n Compute flow f with minimum total cost: min w(f) = e E w(e) f(e) n That is, find a minimum-cost flow among all the flows of maximum value f n Sometimes, given a fixed flow f, compute minimum-cost flow with flow value = f. Solving min-cost flow uses augmented cycles concept. 9/29/2020 6: 46 PM Maximum Flow 20

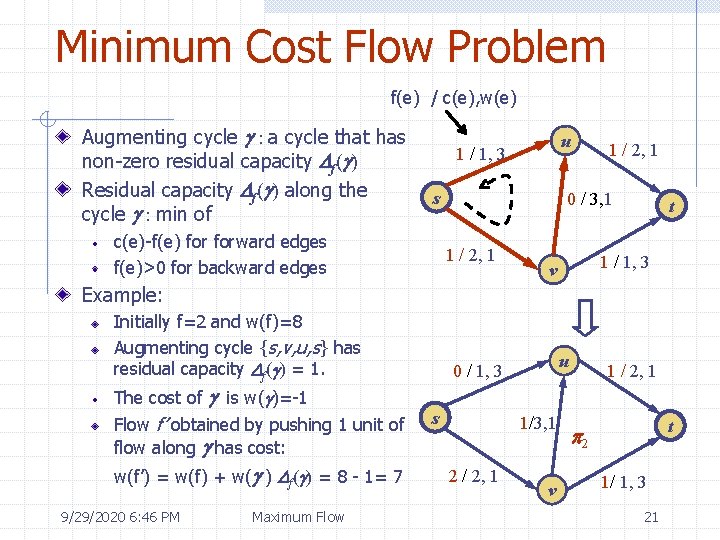
Minimum Cost Flow Problem f(e) / c(e), w(e) Augmenting cycle : a cycle that has non-zero residual capacity Df( ) Residual capacity Df( ) along the cycle : min of u 1 / 1, 3 s c(e)-f(e) forward edges f(e)>0 for backward edges 1 / 2, 1 0 / 3, 1 1 / 2, 1 t 1 / 1, 3 v Example: Initially f=2 and w(f)=8 Augmenting cycle {s, v, u, s} has residual capacity Df( ) = 1. The cost of is w( )=-1 Flow f’ obtained by pushing 1 unit of flow along has cost: w(f’) = w(f) + w( ) Df( ) = 8 - 1= 7 9/29/2020 6: 46 PM Maximum Flow u 0 / 1, 3 s 1/3, 1 2 / 2, 1 v 1 / 2, 1 t p 2 1/ 1, 3 21