MAXIMUM FLOW by Eric Wengert Overview Flow network

MAXIMUM FLOW by Eric Wengert

Overview � Flow network � Maximum Flow � Ford-Fulkerson method �Max-flow min cut theorem �Edmund’s Karp algorithm �Maximum bipartite matching � Push Relabel Algorithm
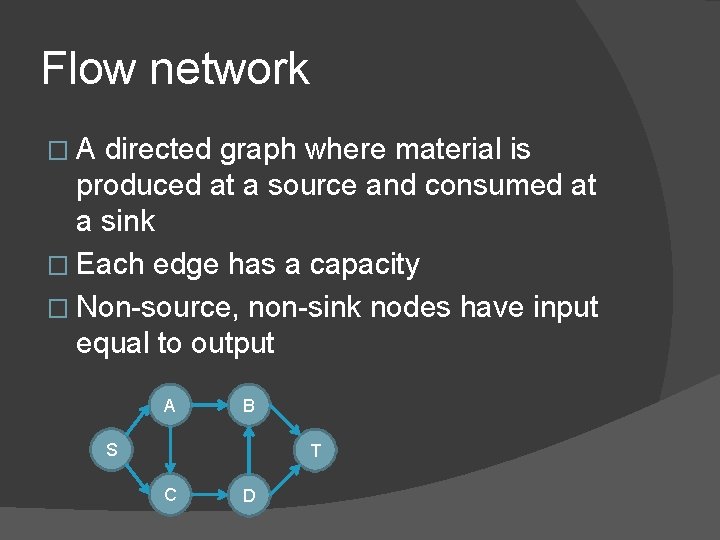
Flow network �A directed graph where material is produced at a source and consumed at a sink � Each edge has a capacity � Non-source, non-sink nodes have input equal to output A B S T C D

Maximum flow � Optimization problem � Compute the greatest rate that material can be shipped from source to sink without violating capacity constraints � A flow is maximum its residual network contains no augmenting path

Ford-Fulkerson method(G, s, t) Initialize flow f to 0 While there exists an augmenting path p in the residual network Gf augment flow f along p Return f Augmenting path – p is a simple path from s to t in the residual network Gf

Basic Ford-Fulkerson algorithm For each edge (u, v) Є G, E (u, v). f = 0 # initialize edge flow to 0 While Ǝ a path p from s to t in residual network cf(p) = min{cf(u, v) : (u, v) is in p} #find min capacity for each edge (u, v) in p if (u, v) Є E (u, v). f = (u, v). f + cf(p) #add flow else (v, u). f = (v, u). f - cf(p)
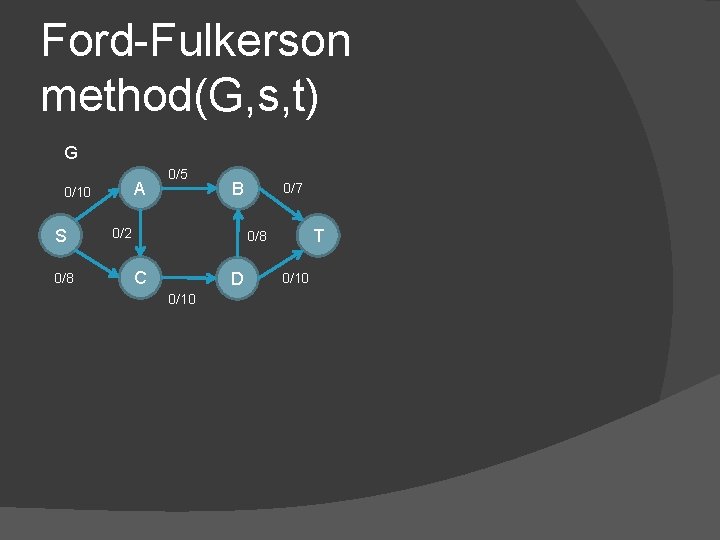
Ford-Fulkerson method(G, s, t) G A 0/10 S 0/8 0/5 B 0/2 0/7 T 0/8 C D 0/10
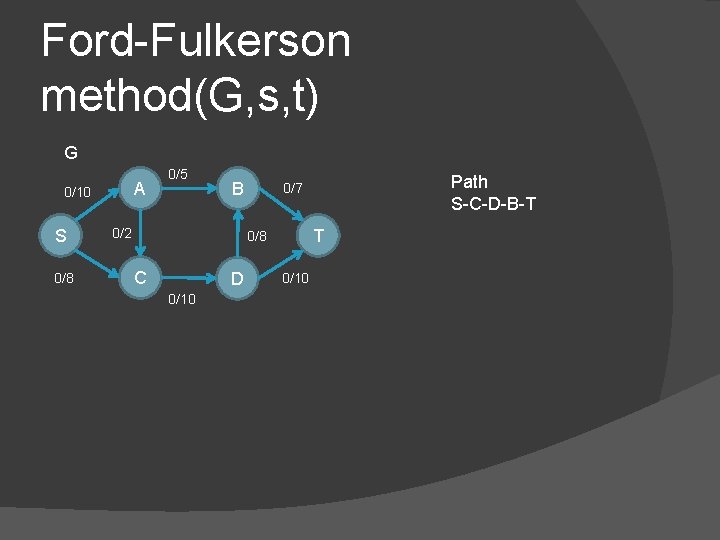
Ford-Fulkerson method(G, s, t) G A 0/10 S 0/8 0/5 B 0/2 T 0/8 C D 0/10 Path S-C-D-B-T 0/7 0/10
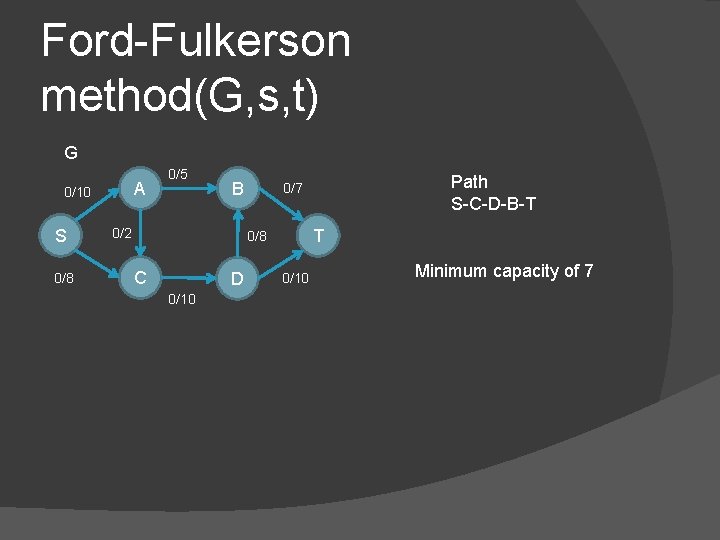
Ford-Fulkerson method(G, s, t) G A 0/10 S 0/8 0/5 B 0/2 T 0/8 C D 0/10 Path S-C-D-B-T 0/7 0/10 Minimum capacity of 7
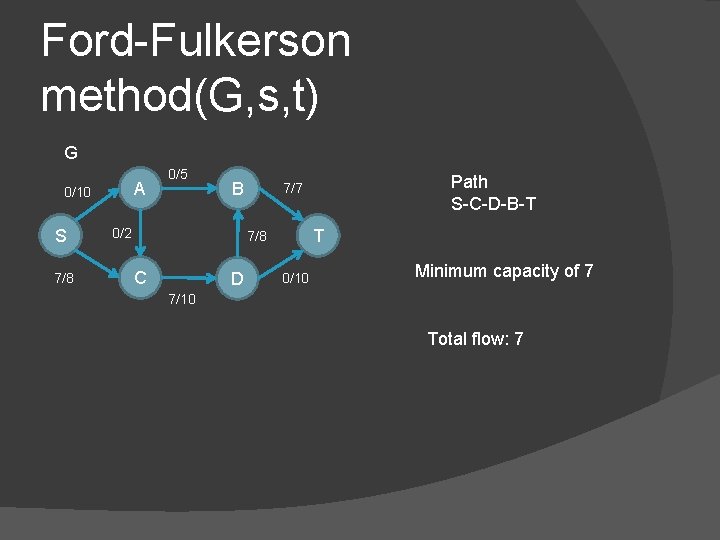
Ford-Fulkerson method(G, s, t) G A 0/10 S 7/8 0/5 B 0/2 T 7/8 C D Path S-C-D-B-T 7/7 0/10 Minimum capacity of 7 7/10 Total flow: 7
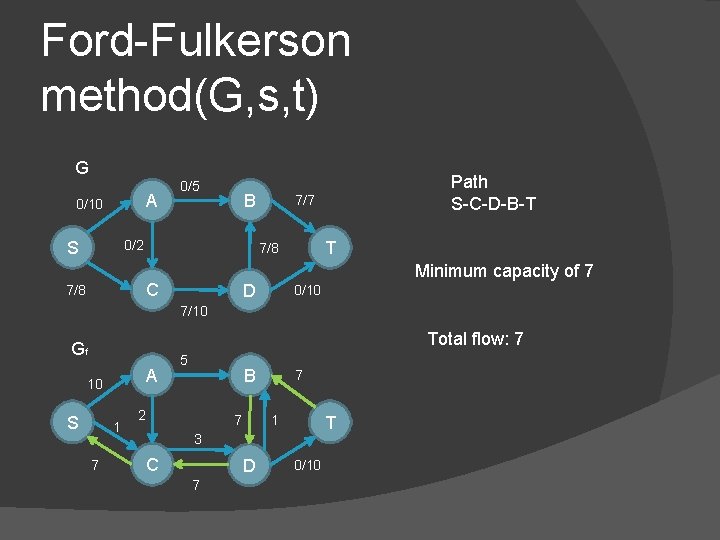
Ford-Fulkerson method(G, s, t) G A 0/10 0/5 B 0/2 S 7/7 T 7/8 C 7/8 Path S-C-D-B-T Minimum capacity of 7 D 0/10 7/10 Total flow: 7 Gf A 10 S 1 7 5 B 2 7 1 7 T 3 C D 7 0/10
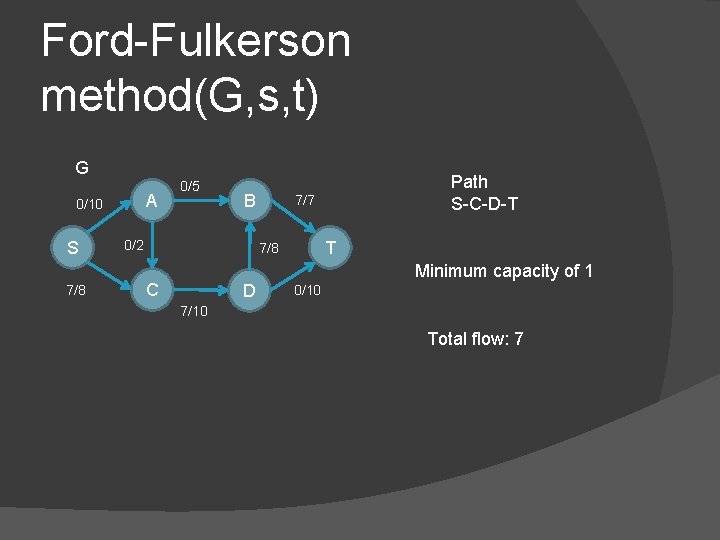
Ford-Fulkerson method(G, s, t) G A 0/10 S 7/8 0/5 B 0/2 7/7 T 7/8 C D Path S-C-D-T Minimum capacity of 1 0/10 7/10 Total flow: 7
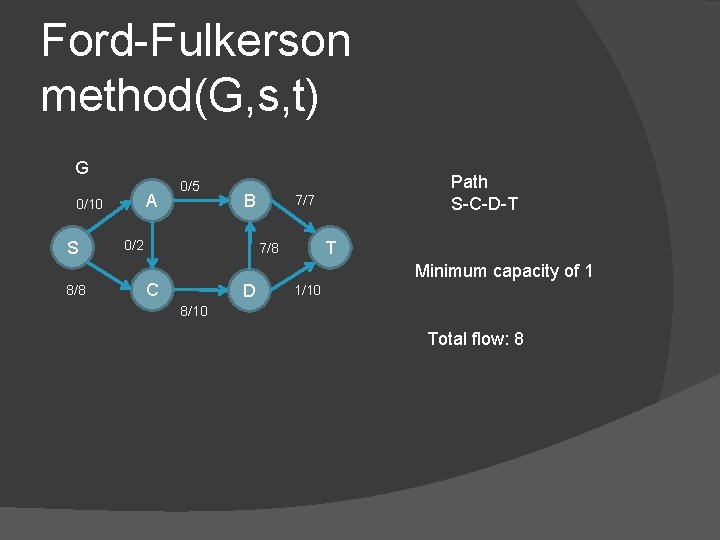
Ford-Fulkerson method(G, s, t) G A 0/10 S 8/8 0/5 B 0/2 7/7 T 7/8 C D Path S-C-D-T Minimum capacity of 1 1/10 8/10 Total flow: 8
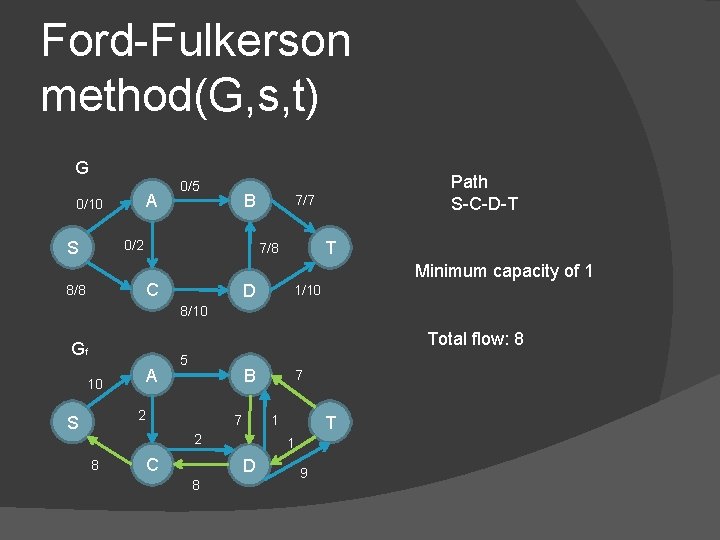
Ford-Fulkerson method(G, s, t) G A 0/10 0/5 B 0/2 S 7/7 T 7/8 C 8/8 Path S-C-D-T Minimum capacity of 1 D 1/10 8/10 Total flow: 8 Gf A 10 5 B 2 S 1 7 2 8 C T 1 D 8 7 9
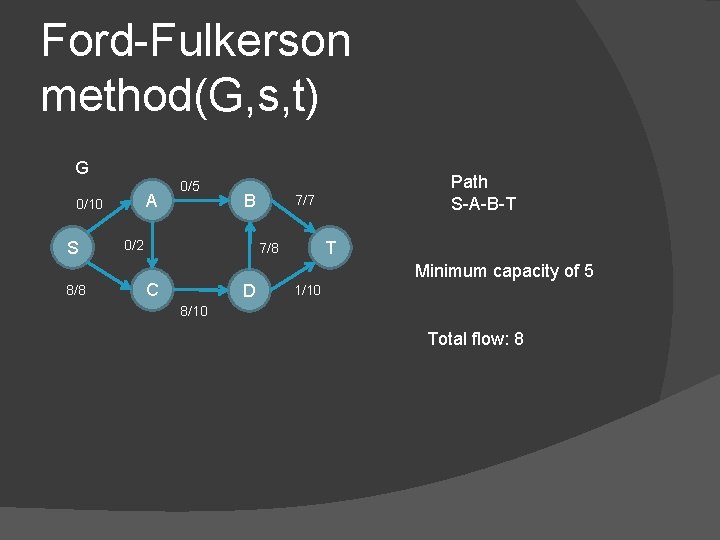
Ford-Fulkerson method(G, s, t) G A 0/10 S 8/8 0/5 B 0/2 7/7 T 7/8 C D Path S-A-B-T Minimum capacity of 5 1/10 8/10 Total flow: 8
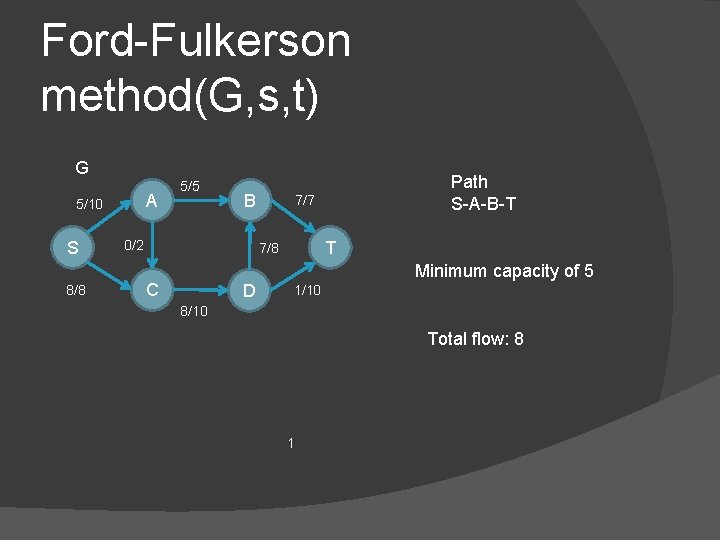
Ford-Fulkerson method(G, s, t) G A 5/10 S 8/8 5/5 B 0/2 7/7 T 7/8 C D Path S-A-B-T Minimum capacity of 5 1/10 8/10 Total flow: 8 1
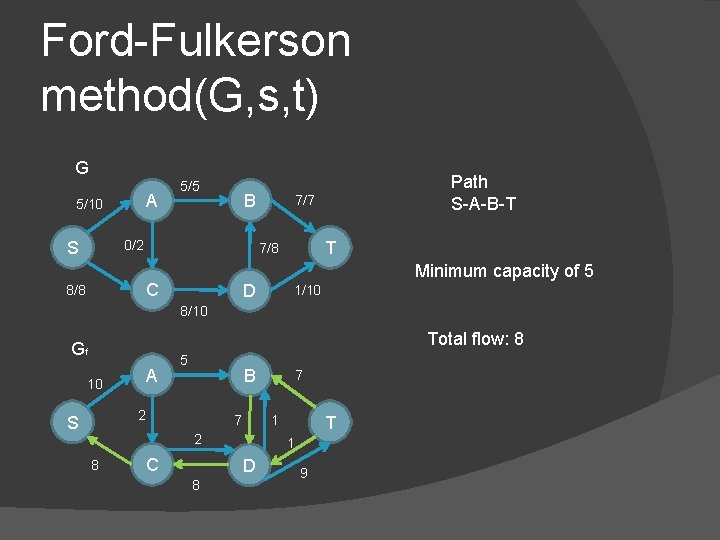
Ford-Fulkerson method(G, s, t) G A 5/10 5/5 B 0/2 S 7/7 T 7/8 C 8/8 Path S-A-B-T Minimum capacity of 5 D 1/10 8/10 Total flow: 8 Gf A 10 5 B 2 S 1 7 2 8 C T 1 D 8 7 9
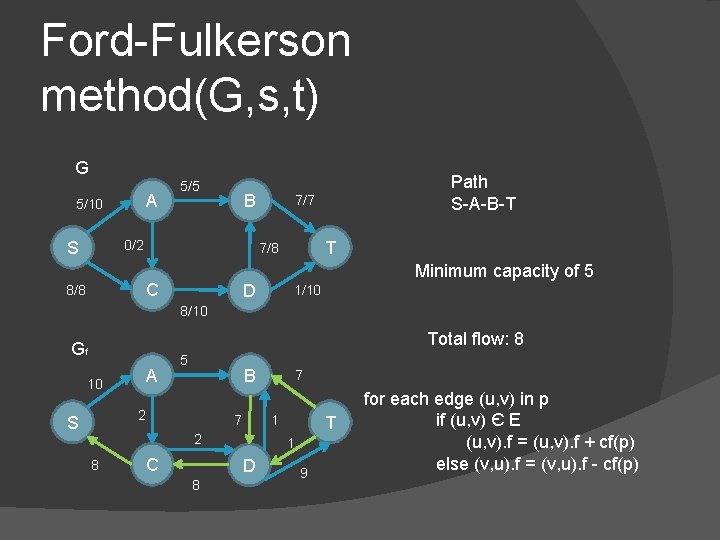
Ford-Fulkerson method(G, s, t) G A 5/10 5/5 B 0/2 S 7/7 T 7/8 C 8/8 Path S-A-B-T Minimum capacity of 5 D 1/10 8/10 Total flow: 8 Gf A 10 5 B 2 S 1 7 2 8 C T 1 D 8 7 9 for each edge (u, v) in p if (u, v) Є E (u, v). f = (u, v). f + cf(p) else (v, u). f = (v, u). f - cf(p)
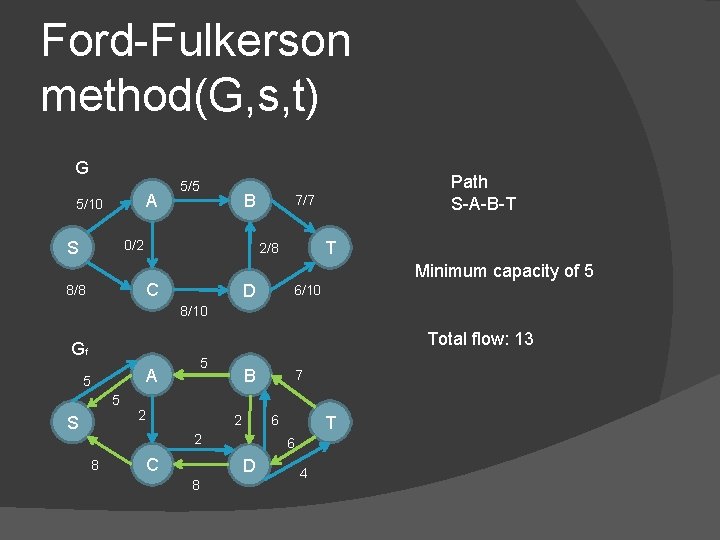
Ford-Fulkerson method(G, s, t) G A 5/10 5/5 B 0/2 S 7/7 T 2/8 C 8/8 Path S-A-B-T Minimum capacity of 5 D 6/10 8/10 Total flow: 13 Gf A 5 5 S 5 2 B 6 2 2 8 C T 6 D 8 7 4
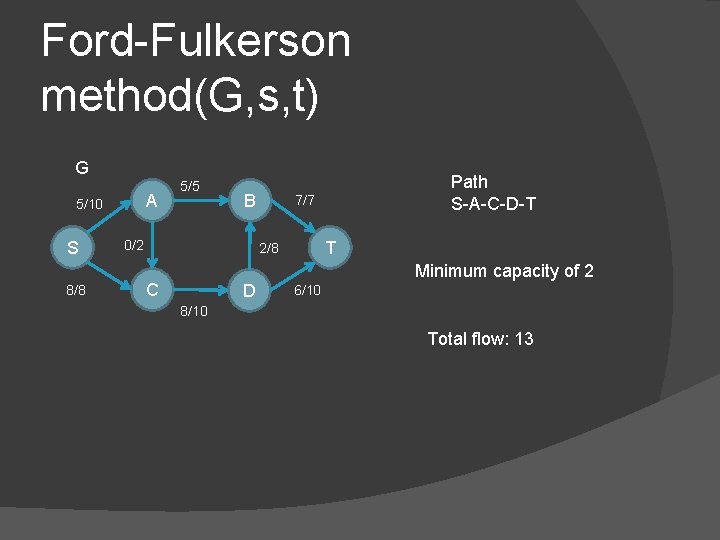
Ford-Fulkerson method(G, s, t) G A 5/10 S 8/8 5/5 B 0/2 7/7 T 2/8 C D Path S-A-C-D-T Minimum capacity of 2 6/10 8/10 Total flow: 13
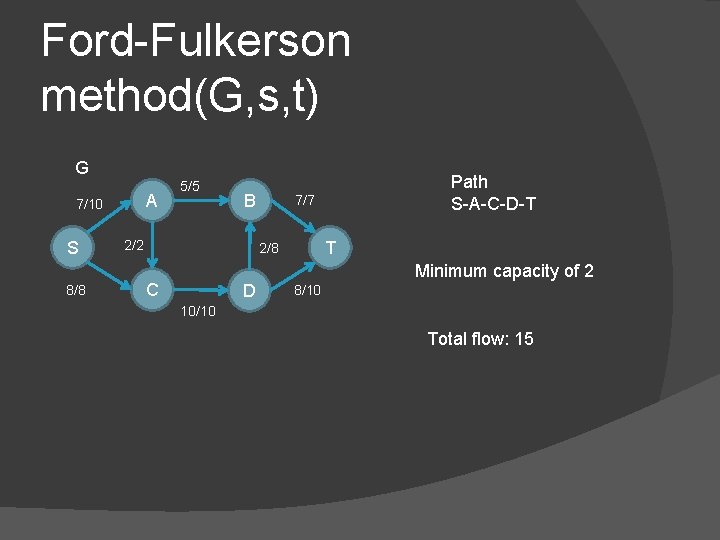
Ford-Fulkerson method(G, s, t) G A 7/10 S 8/8 5/5 B 2/2 7/7 T 2/8 C D Path S-A-C-D-T Minimum capacity of 2 8/10 10/10 Total flow: 15
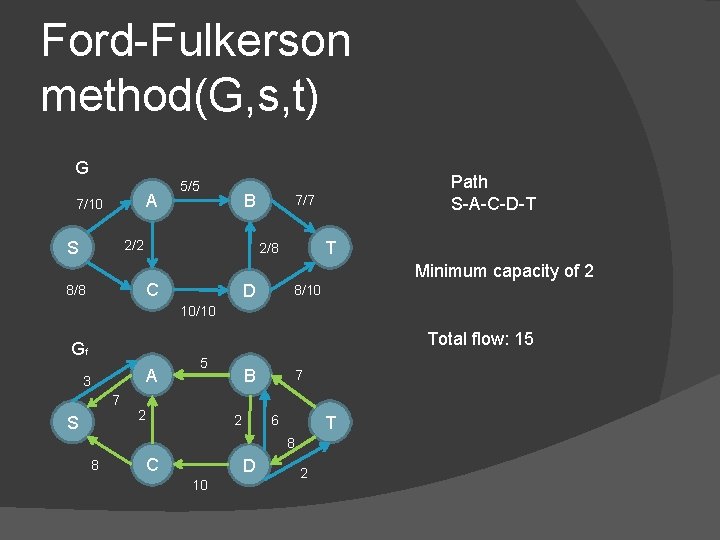
Ford-Fulkerson method(G, s, t) G A 7/10 5/5 B 2/2 S 7/7 T 2/8 C 8/8 Path S-A-C-D-T Minimum capacity of 2 D 8/10 10/10 Total flow: 15 Gf A 3 7 S 5 2 B 7 6 2 T 8 8 C D 10 2

Time complexity Find augmenting path O(E) 2. Compute bottleneck capacity 3. Augment each edge and total flow Max number of iterations O(f) O(Ef) 1.

Max-flow min-cut theorem � Max flow = min cut G A 7 S 5 B 2 C 8 7 T 2 D 10 8 15 19 15 15 Total flow: 15

Edmonds-Karp algorithm Ford-Fulkerson altered by finding the augmented path with a breadth-first search � Choose shortest path from s to t in the residual network � Time Complexity � Breadth-first search O(E) � Total number of flow augmentations O(VE) � O(VE 2)
Maximum bipartite matching
Maximum bipartite matching

Maximum bipartite matching � Finding a path from s to t using DFS or BFS O(E) � Value of maximum flow to t O(V) � O(VE)

Push Relabel � Flow from higher point to lower point � Source is highest h = |v| � Sink is lowest h = 0 � Source pushes maximum flow onto edges � Height increased to allow flow out � Increasing the height is called relabel

Push Relabel algorithm Initialize preflow to 0 While Ǝ an applicable push or relabel operation select an applicable push or relabel operation and perform it
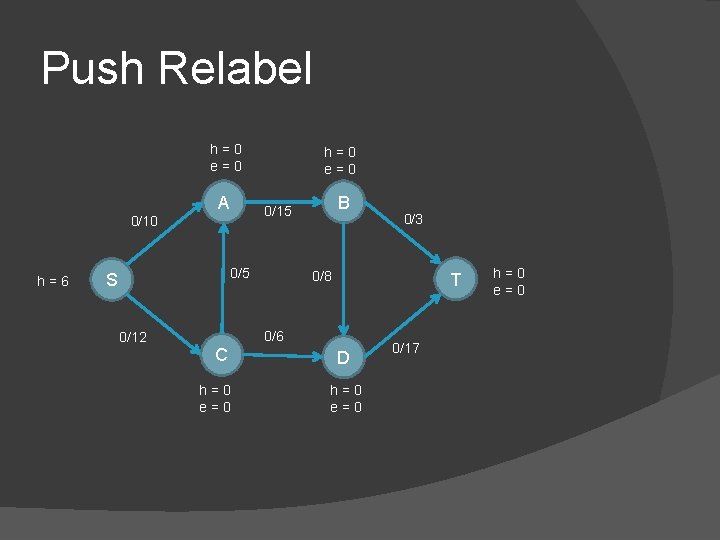
Push Relabel h=0 e=0 A 0/5 S B 0/15 0/10 h=6 h=0 e=0 0/8 T 0/6 0/12 C h=0 e=0 0/3 D h=0 e=0 0/17 h=0 e=0
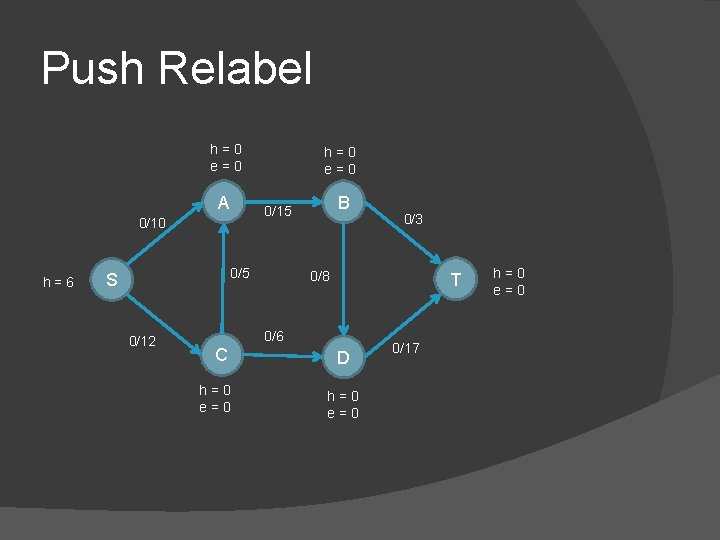
Push Relabel h=0 e=0 A 0/5 S 0/12 B 0/15 0/10 h=6 h=0 e=0 0/8 T 0/6 C h=0 e=0 0/3 D h=0 e=0 0/17 h=0 e=0
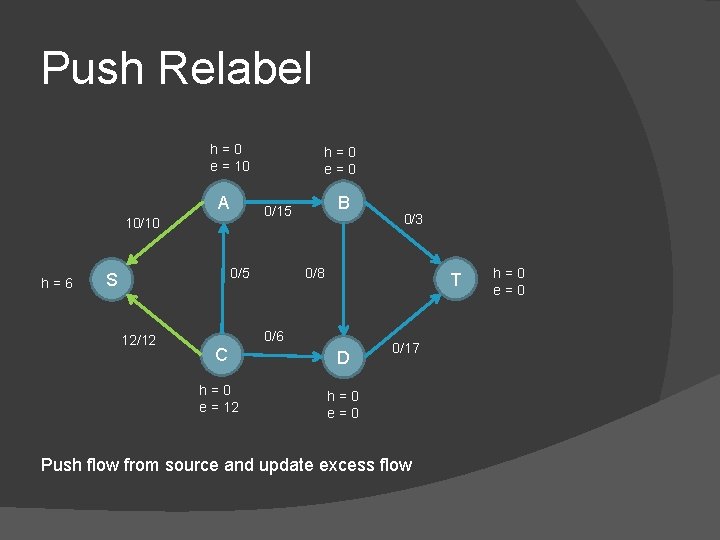
Push Relabel h=0 e = 10 A 0/5 S 12/12 B 0/15 10/10 h=6 h=0 e=0 0/3 0/8 T 0/6 C D h=0 e = 12 h=0 e=0 0/17 Push flow from source and update excess flow h=0 e=0
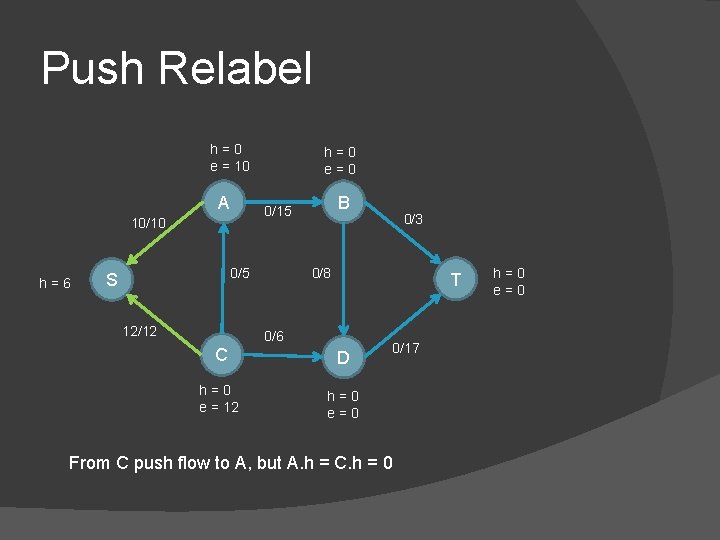
Push Relabel h=0 e = 10 A 0/5 S B 0/15 10/10 h=6 h=0 e=0 12/12 0/3 0/8 T 0/6 C D h=0 e = 12 h=0 e=0 0/17 From C push flow to A, but A. h = C. h = 0 h=0 e=0
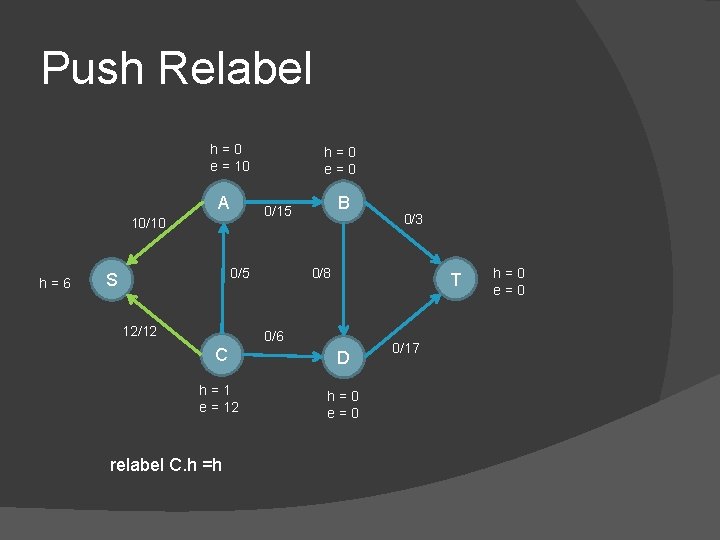
Push Relabel h=0 e = 10 A 0/5 S B 0/15 10/10 h=6 h=0 e=0 12/12 0/8 T 0/6 C D h=1 e = 12 h=0 e=0 relabel C. h =h 0/3 0/17 h=0 e=0
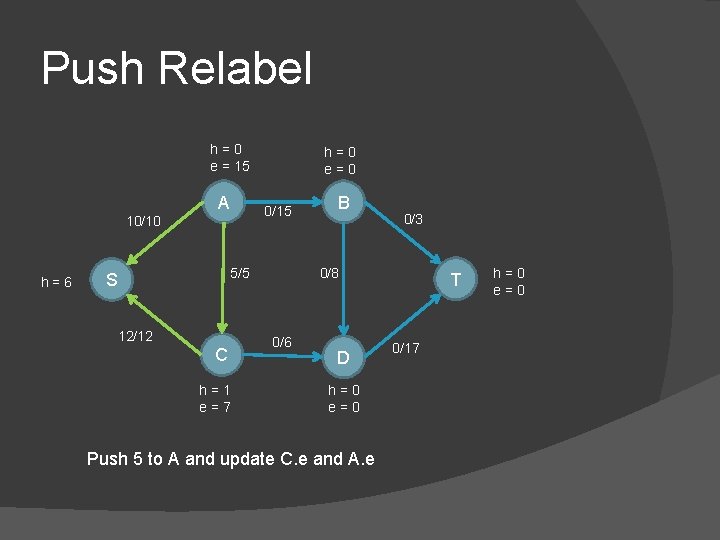
Push Relabel h=0 e = 15 A 0/15 10/10 h=6 h=0 e=0 5/5 S 12/12 C h=1 e=7 B 0/3 0/8 0/6 D h=0 e=0 Push 5 to A and update C. e and A. e T 0/17 h=0 e=0
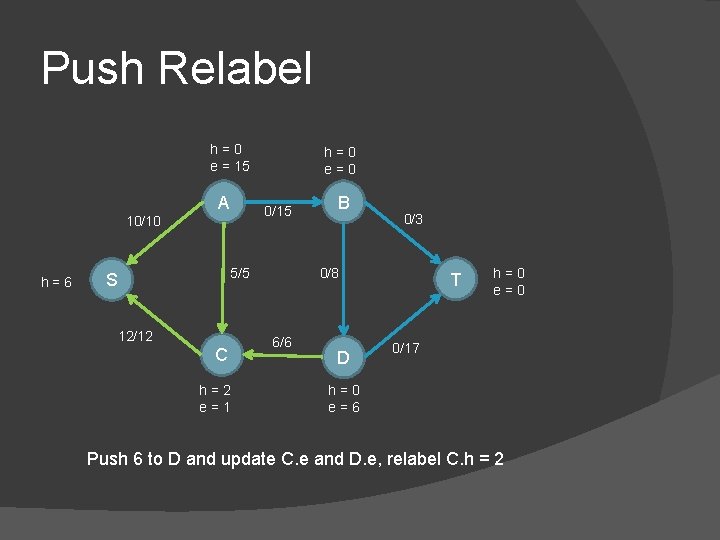
Push Relabel h=0 e = 15 A 0/15 10/10 h=6 h=0 e=0 5/5 S 12/12 C h=2 e=1 B 0/3 0/8 6/6 D T h=0 e=0 0/17 h=0 e=6 Push 6 to D and update C. e and D. e, relabel C. h = 2
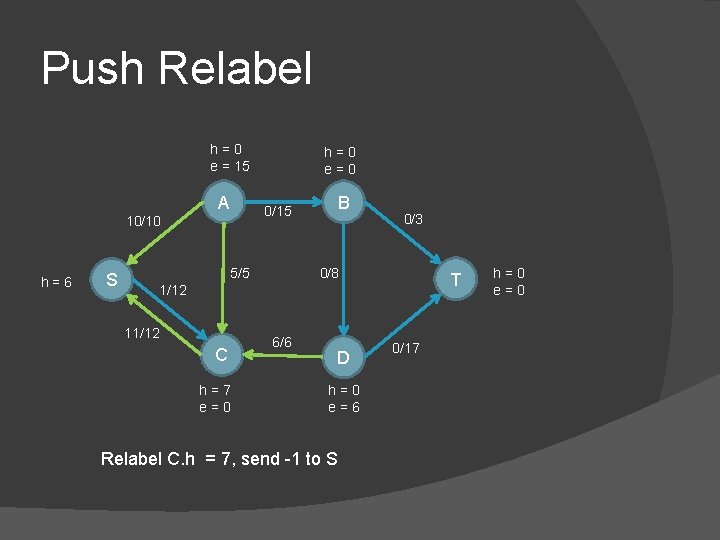
Push Relabel h=0 e = 15 A S B 0/15 10/10 h=6 h=0 e=0 5/5 0/3 0/8 T 1/12 11/12 C h=7 e=0 6/6 D h=0 e=6 Relabel C. h = 7, send -1 to S 0/17 h=0 e=0
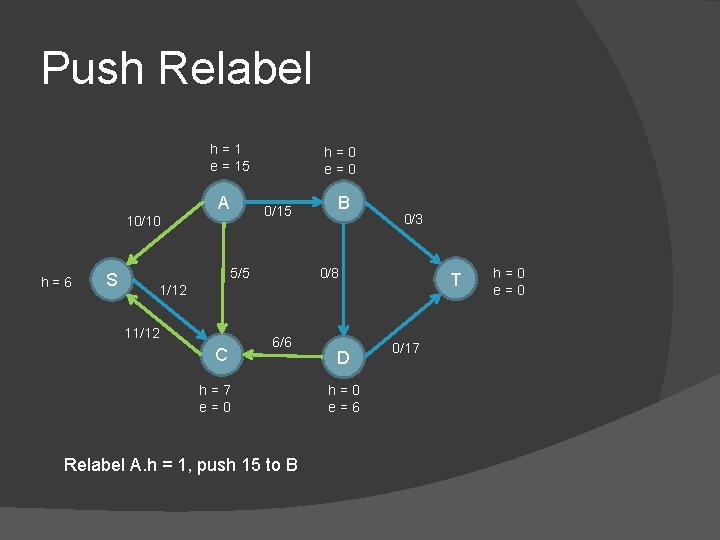
Push Relabel h=1 e = 15 A 0/15 10/10 h=6 S h=0 e=0 5/5 B 0/3 0/8 T 1/12 11/12 C 6/6 h=7 e=0 Relabel A. h = 1, push 15 to B D h=0 e=6 0/17 h=0 e=0
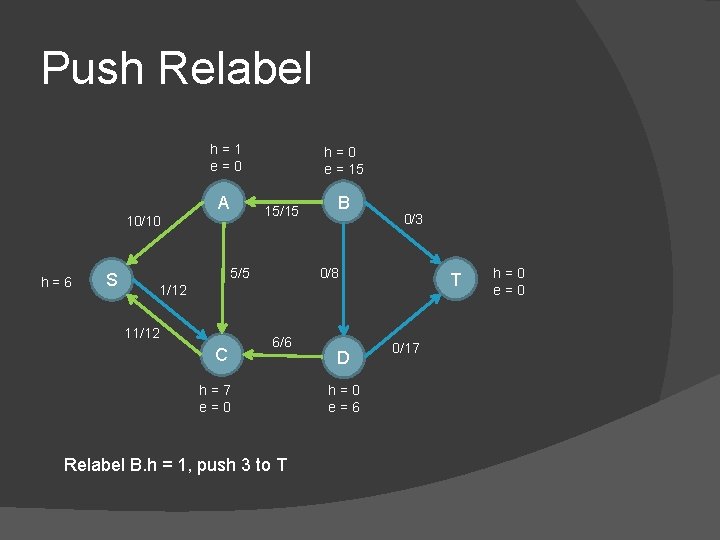
Push Relabel h=1 e=0 A 15/15 10/10 h=6 S h=0 e = 15 5/5 B 0/3 0/8 T 1/12 11/12 C 6/6 h=7 e=0 Relabel B. h = 1, push 3 to T D h=0 e=6 0/17 h=0 e=0
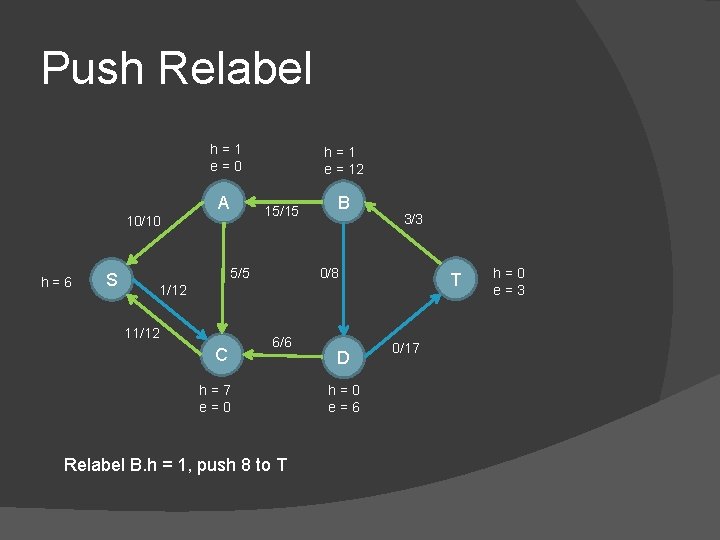
Push Relabel h=1 e=0 A 15/15 10/10 h=6 S h=1 e = 12 5/5 B 3/3 0/8 T 1/12 11/12 C 6/6 h=7 e=0 Relabel B. h = 1, push 8 to T D h=0 e=6 0/17 h=0 e=3
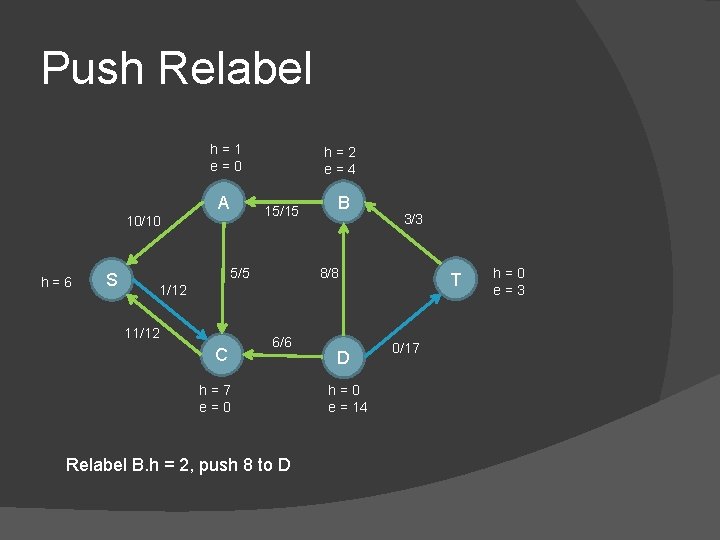
Push Relabel h=1 e=0 A 15/15 10/10 h=6 S h=2 e=4 5/5 B 3/3 8/8 T 1/12 11/12 C 6/6 h=7 e=0 Relabel B. h = 2, push 8 to D D h=0 e = 14 0/17 h=0 e=3
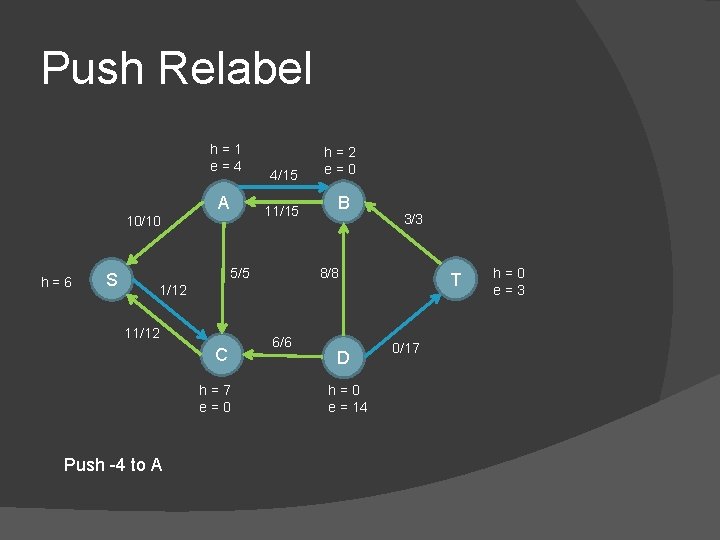
Push Relabel h=1 e=4 A 10/10 h=6 S 4/15 h=2 e=0 11/15 B 5/5 3/3 8/8 T 1/12 11/12 C h=7 e=0 Push -4 to A 6/6 D h=0 e = 14 0/17 h=0 e=3
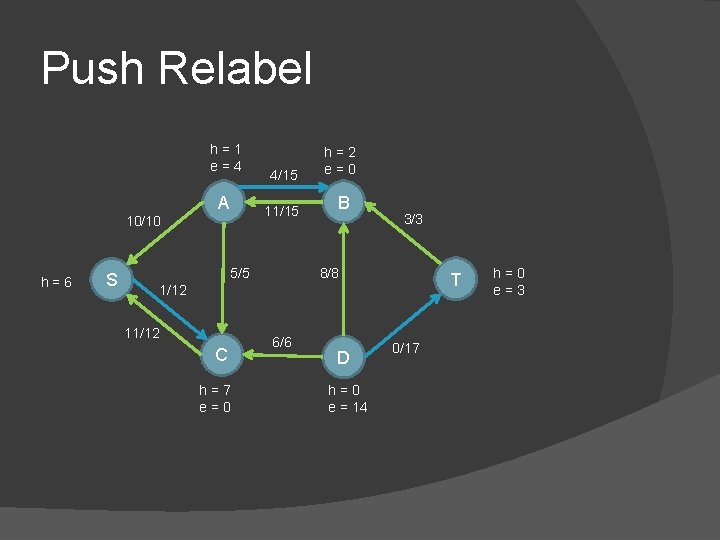
Push Relabel h=1 e=4 A 10/10 h=6 S 4/15 h=2 e=0 11/15 B 5/5 3/3 8/8 T 1/12 11/12 C h=7 e=0 6/6 D h=0 e = 14 0/17 h=0 e=3
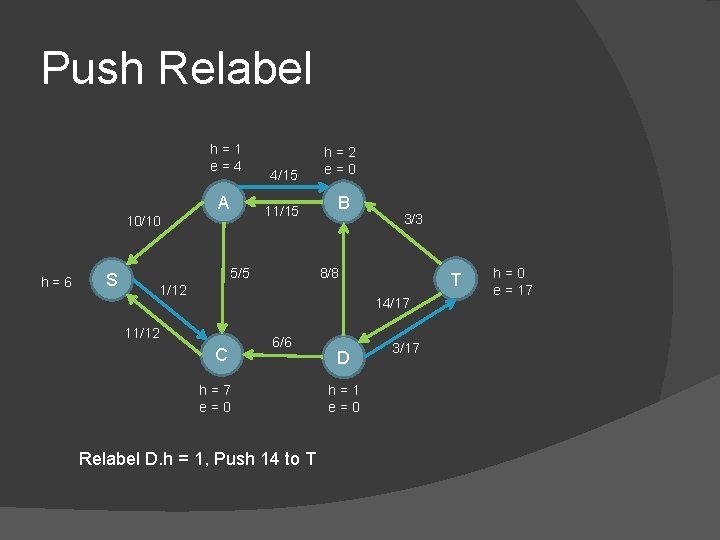
Push Relabel h=1 e=4 A 10/10 h=6 S 4/15 h=2 e=0 11/15 B 5/5 3/3 8/8 1/12 T 14/17 11/12 C 6/6 h=7 e=0 Relabel D. h = 1, Push 14 to T D h=1 e=0 3/17 h=0 e = 17
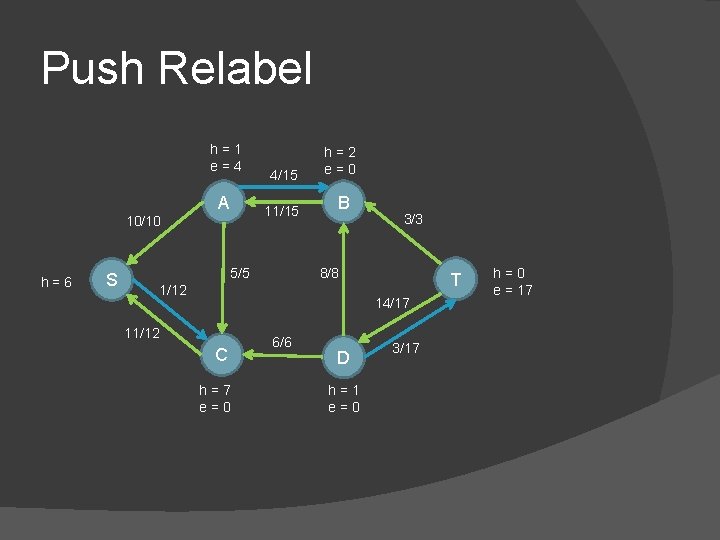
Push Relabel h=1 e=4 A 10/10 h=6 S 4/15 h=2 e=0 11/15 B 5/5 3/3 8/8 1/12 T 14/17 11/12 C h=7 e=0 6/6 D h=1 e=0 3/17 h=0 e = 17
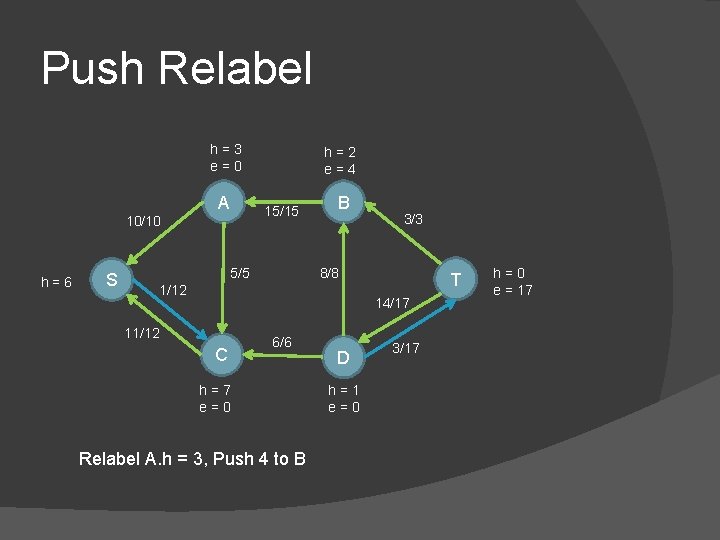
Push Relabel h=3 e=0 A 15/15 10/10 h=6 S h=2 e=4 5/5 B 3/3 8/8 1/12 T 14/17 11/12 C 6/6 h=7 e=0 Relabel A. h = 3, Push 4 to B D h=1 e=0 3/17 h=0 e = 17
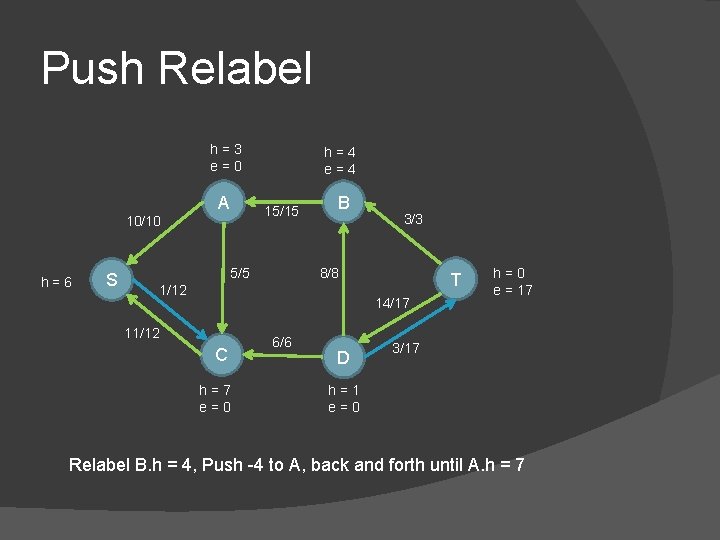
Push Relabel h=3 e=0 A 15/15 10/10 h=6 S h=4 e=4 5/5 B 3/3 8/8 1/12 T 14/17 11/12 C h=7 e=0 6/6 D h=0 e = 17 3/17 h=1 e=0 Relabel B. h = 4, Push -4 to A, back and forth until A. h = 7
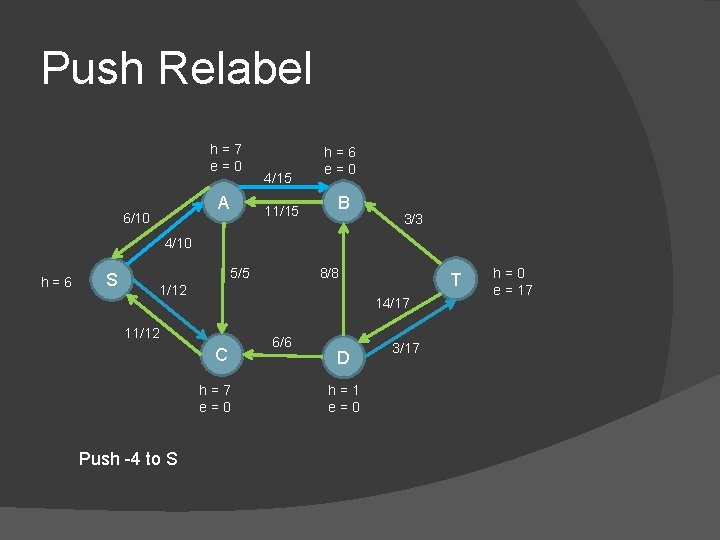
Push Relabel h=7 e=0 A 6/10 4/15 11/15 h=6 e=0 B 3/3 4/10 h=6 S 5/5 8/8 1/12 14/17 11/12 C h=7 e=0 Push -4 to S T 6/6 D h=1 e=0 3/17 h=0 e = 17

Push Relabel time complexity O(V 2) Relabels O(VE) Saturating pushes O(V 2 E) Non-saturating pushes Data structures can be designed to pick and execute an operation in O(1) O(V 2 E) time complexity

References � Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein, (3 rd edition), Mc Graw Hill Ford Fulkerson method example � https: //www. hackerearth. com/practice/algorithms/gra phs/maximum-flow/tutorial/ Push Relabel example by Ditixa Vyas � https: //www. youtube. com/watch? v=xcq. Zy. G 9 CEAw
- Slides: 51