Maximum Flow Algorithms ACM 1 Maxflow mincut theorem

Maximum Flow Algorithms —— ACM 黄宇翔

目录 1 Max-flow min-cut theorem 2 Augmenting path algorithms 3 Push-relabel maximum flow algorithm

Maximum flow problem l source : s, sink : t l for any (u, v), (v, u) does not exist and c(u, v) > 0 l for any vertex v, there's a path s→v→t l the flow f : V × V → R, satisfies two properties : • for any (u, v), 0 ≤ f (u, v) ≤ c (u, v) • for any u ∈ V - {s, t}, ∑ f (u, v) = ∑ f (v, u) l | f | = ∑ f (s, v) - ∑ f (v, s), we want it max

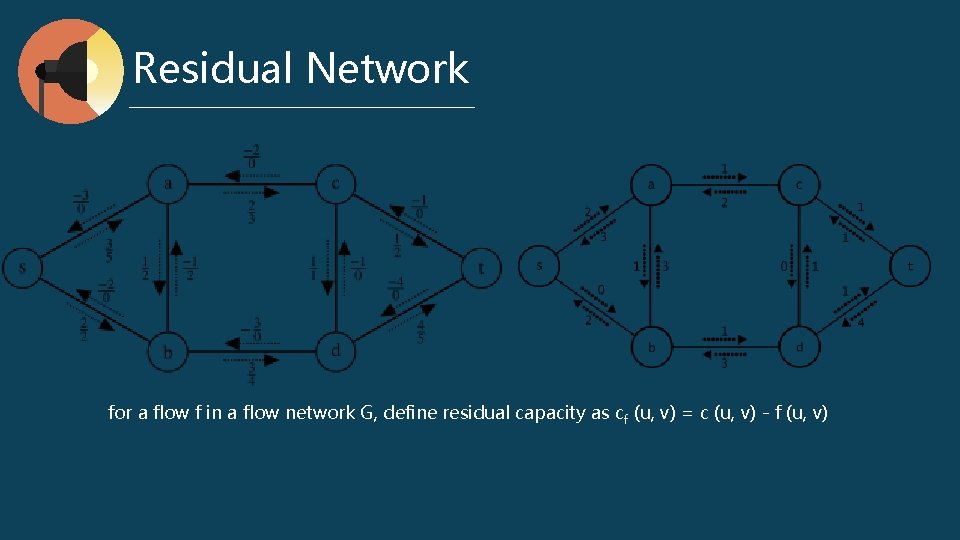
Residual Network for a flow f in a flow network G, define residual capacity as c f (u, v) = c (u, v) - f (u, v)

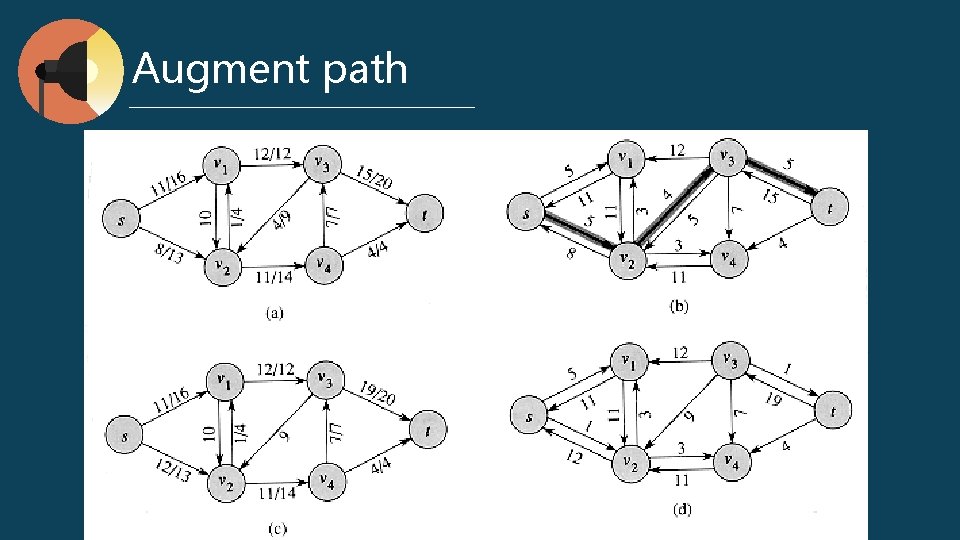
Augment path

Lemma l f is a flow on G l Gf is the residual network induced from f l Δf is a flow on Gf l we define a new flow on G : f ↑ Δf l for any (u, v), (f ↑ Δf) (u, v) = f (u, v) + Δf (u, v) - Δf (v, u) l then we have : | f ↑ Δf | = | f | + | Δf |

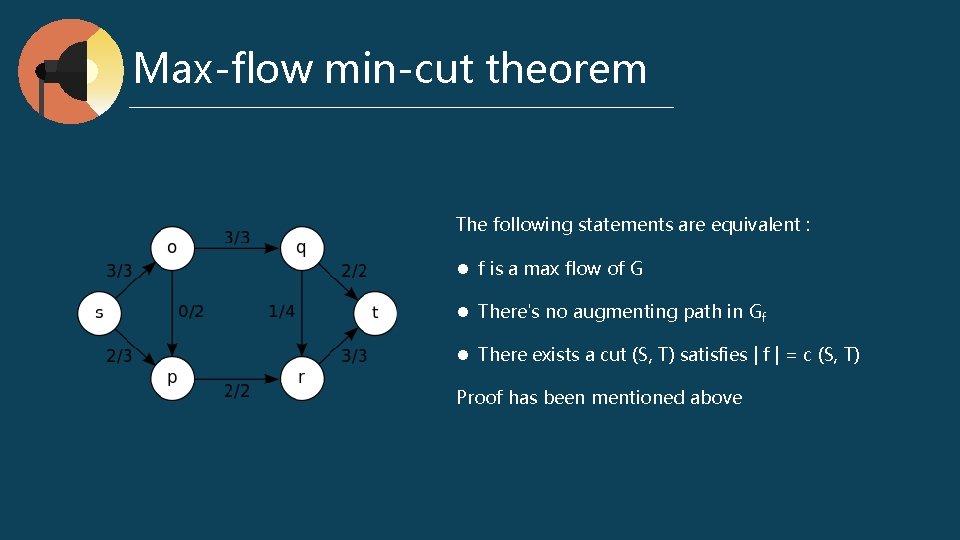
Cut Definitions : l a cut (S, T) is a partition of V which satisfies : s ∈ S and t ∈ T l f (S, T) = ∑ ∑ f (u, v) - ∑ ∑ f (v, u) l c (S, T) = ∑ ∑ c (u, v) Properties : l for any cut (S, T), f (S, T) = | f | l for any cut (S, T), f (S, T) ≤ c (S, T)

Max-flow min-cut theorem The following statements are equivalent : l f is a max flow of G l There's no augmenting path in Gf l There exists a cut (S, T) satisfies | f | = c (S, T) Proof has been mentioned above

Augmenting path algorithms l Ford-Fulkerson : O ( E | f* | ) l Edmonds-Karp : O ( V E 2 ) l SAP (= shortest augmenting path) : O ( V 2 E ) l Dinic : O ( V 2 E ) l ISAP (= improved shortest augmenting path) : O ( V 2 E ) (GAP)

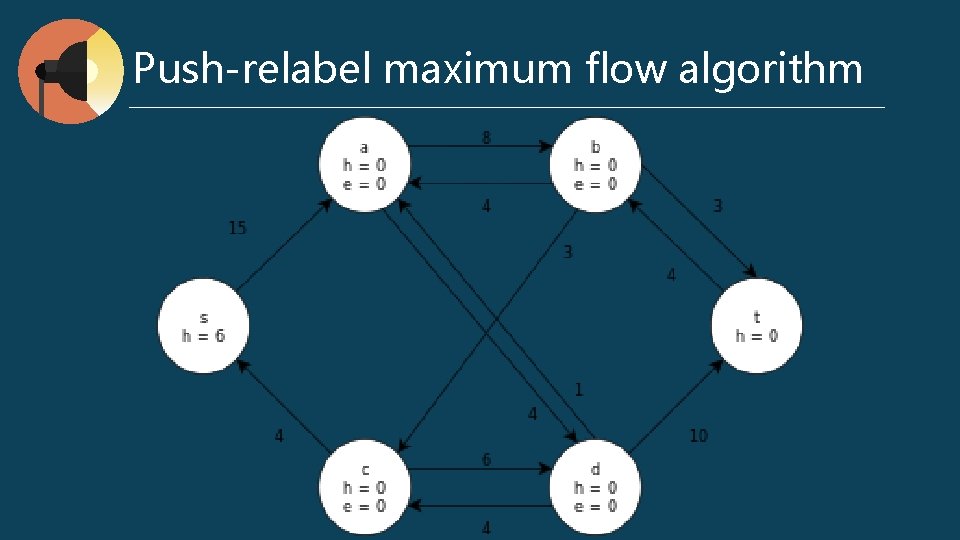
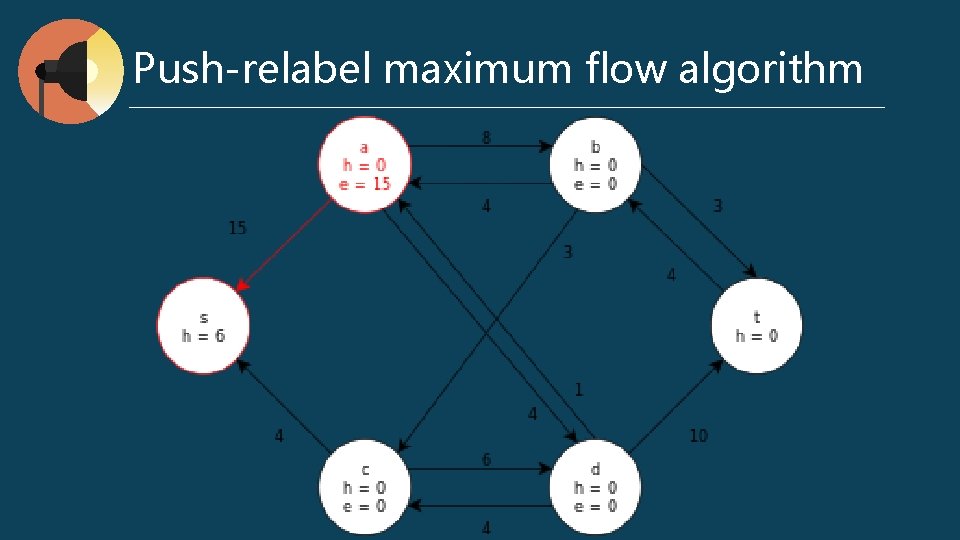
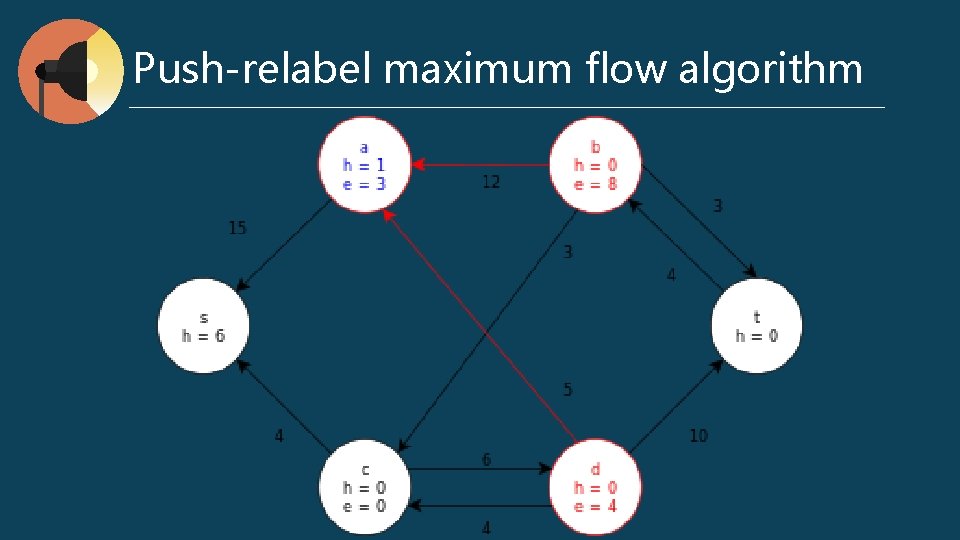
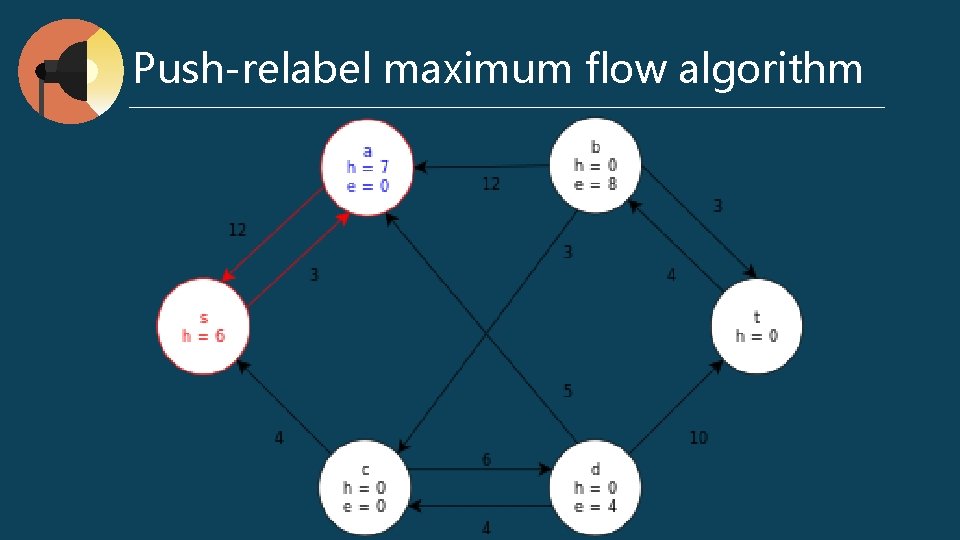
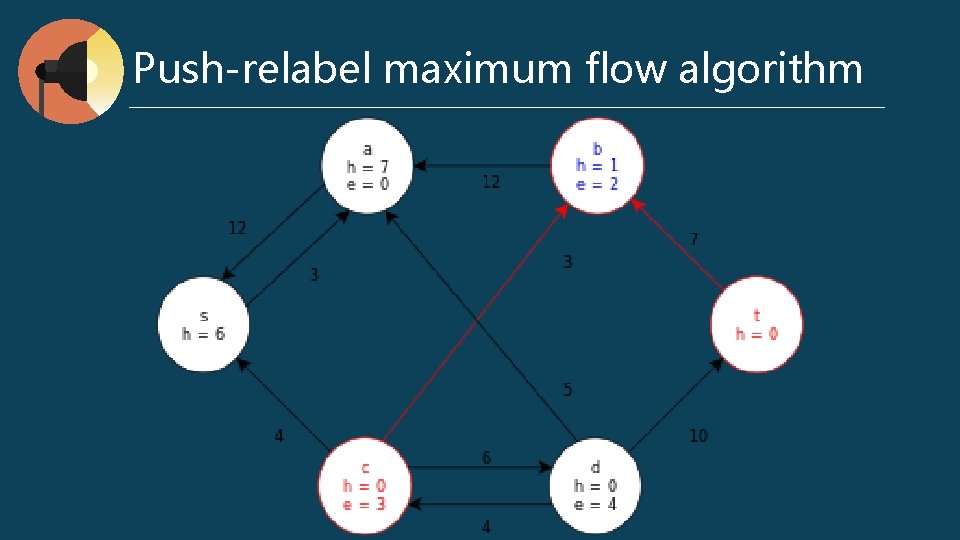
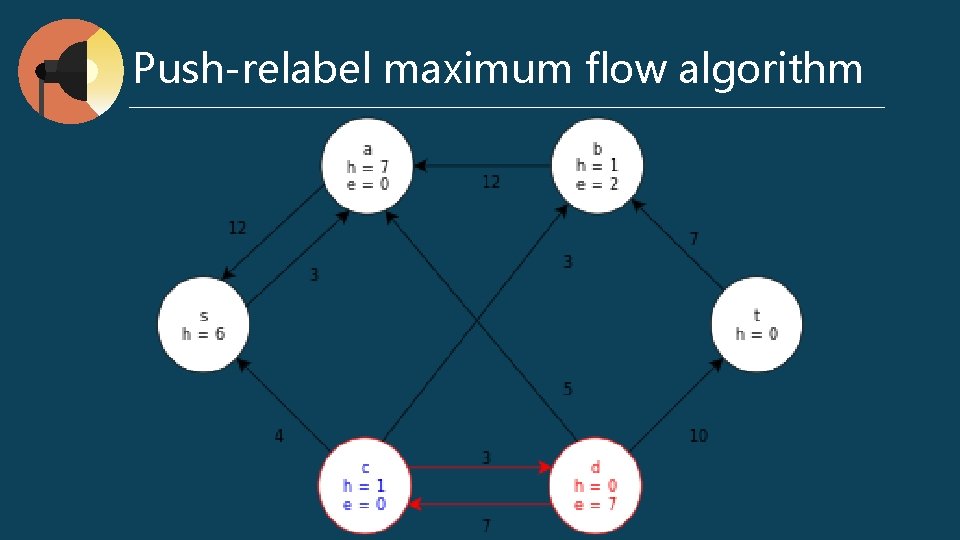
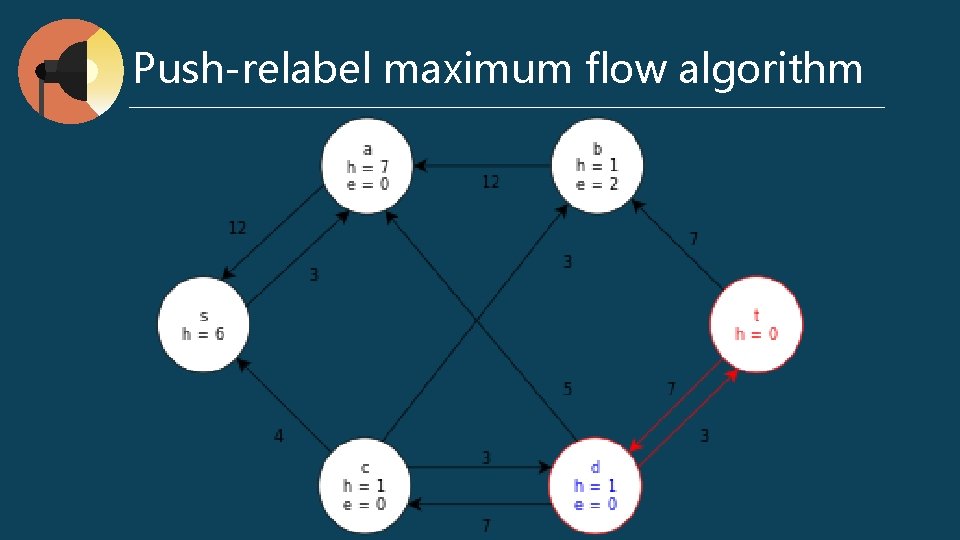
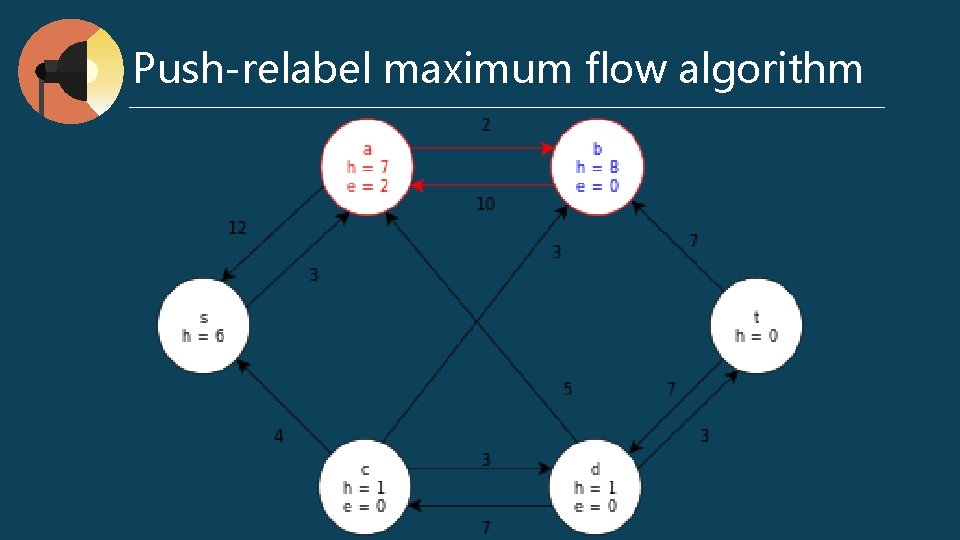
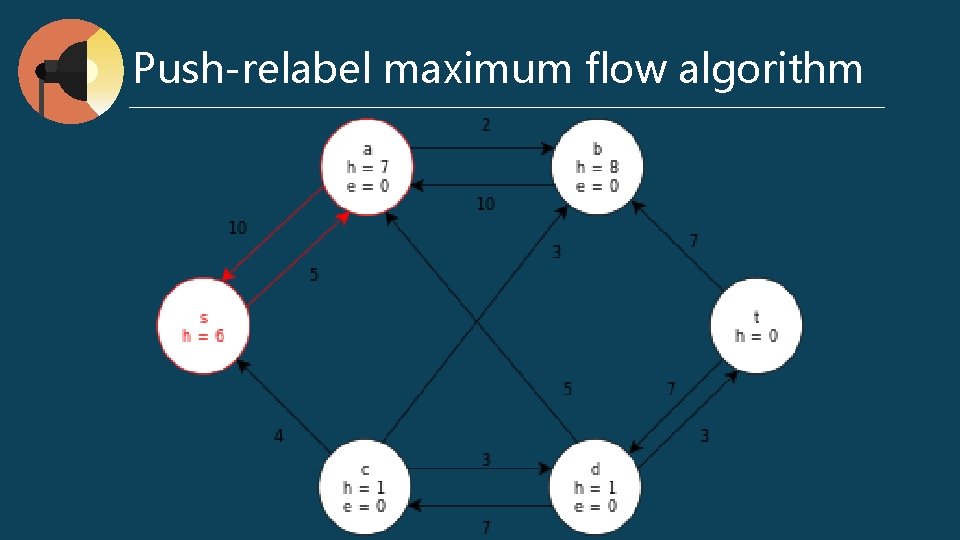
Push-relabel maximum flow algorithm preflow : for any v ∈ V, ∑ f (v, u) - ∑ f (u, v) ≥ 0 excess flow e (u) = ∑ f (v, u) - ∑ f (u, v) h (u) : the shortest distance to t Push (u, v) // when e (u) > 0, cf (u, v) > 0, and u. h = v. h + 1 Δf (u, v) = min (e (u), cf (u, v)) if (u, v) ∈ E f (u, v) += Δf (u, v) else f (u, v) -= Δf (u, v) e (u) -= Δf (u, v) v (u) += Δf (u, v) l Relabel (u) // when e (u) > 0, for all (u, v) ∈ Ef, h (u) <= h (v) h (u) = min (h (v)) l l

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Push-relabel maximum flow algorithm

Thanks for listening 2021/12/28