MAXIMISER les RESULTATS La mthode du simplexe MISE

MAXIMISER les RESULTATS La méthode du simplexe

MISE en FORME MATHÉMATIQUE n n Définir les variables de décision n ensemble des variables qui régissent la situation à modéliser n variables réelles, entières, binaires Préciser la fonction objectif n fonction mathématique composée des variables de décision qui représente le modèle physique modélisé n fonction linéaire, non-linéaire Préciser les contraintes du problème n ensemble des paramètres qui limitent le modèle réalisable n équations ou inéquations composées des variables de décision Préciser les paramètres du modèle n constantes associées aux contraintes et à la fonction objective

FORMULATION MATHÉMATIQUE n n FONCTION OBJECTIF n Maximiser ou minimiser n z = c 1 x 1 + c 2 x 2 + c 3 x 3 + … + + c n xn Contraintes n a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 nxn ( , =, ) b 1 n a 21 x 1 + a 22 x 2 + a 23 x 3 + … + a 2 nxn ( , =, ) b 2 n am 1 x 1 + am 2 x 2 + am 3 x 3 + … + amnxn ( , =, ) bm Contraintes de non-négativité n xj 0 ; j = 1, 2, 3, … n avec n xj variables de décision (inconnues) n aij, bi, cj paramètres du programme linéaire

TERMINOLOGIE du MODÈLE n n n Activités n Ensemble des actes et opérations à effectuer n j = 1, …n activités Ressources n Moyens disponibles pour effectuer les activités n bi, i = 1, …m ressources Quantité requise de ressource n Quantité unitaire de ressources consommées pour chaque activité aij Niveau activation n Quantité de ressources affectée à une activité n xj = niveau d’activation de l’activité j Coût ou profit n Mesure de performance de l’allocation des ressources aux activités cj

TERMINOLOGIE de la SOLUTION n Solution réalisable n n Zone de solution n n Solution où toutes les contraintes du modèle sont satisfaites Ensemble de toutes les solutions réalisables Solution optimale Solution réalisable où la fonction objectif atteint la meilleure valeur, maximum ou minimum n Plusieurs solutions optimales possibles n

EXEMPLE: PROBLÈME d'ALLOCATION de RESSOURCES Vous disposez de n 8 kg de pommes n 2, 5 kg de pâte n 6 plaques pour confectionner des chaussons et des tartes Pour faire un chausson, il vous faut: n 150 g de pommes n et 75 g de pâte Chaque chausson est vendu 3 € Pour faire une tarte, il vous faut n 1 kg de pommes n 200 g de pâte n et 1 plaque Chaque tarte est divisée en 6 parts vendues chacune 2 € Que faut-il cuisiner pour maximiser le chiffre d'affaires de la vente ?

PROBLÈME d'ALLOCATION de RESSOURCES Définissons 2 variables de décision n x 1 : le nombre de chaussons confectionnés n x 2 : le nombre de tartes confectionnées Le chiffre d’affaires associé à une production (x 1; x 2) est z = 3 x 1 + (6 x 2)x 2 = 3 x 1 + 12 x 2 Il ne faut pas utiliser plus de ressources que disponibles n 150 x 1 + 1000 x 2 8000 (pommes) n 75 x 1 + 200 x 2 2500 (pâte) n x 2 6 (plaques) On ne peut pas cuisiner des quantités négatives : x 1 et x 2 0

MODÈLE: PROBLÈME d'ALLOCATION de RESSOURCES Pour maximiser le chiffre d’affaires de la vente, il faut déterminer les nombres x 1 et x 2 de chaussons et de tartes a cuisiner, solution du problème Max z = 3 x 1 + 12 x 2 Sujet à n 150 x 1 + 1000 x 2 8000 n 75 x 1 + 200 x 2 2500 n x 2 6 n x 1 ; x 2 0 En fait, il faudrait également imposer à x 1 et x 2 de ne prendre que des valeurs entières

RÉSOLUTION GRAPHIQUE Zone limitée par l’ensemble des équations de contraintes du problème et par les limites des variables de décision x 2 8 6 4 2 0 2 4 6 8 10 x 1

MÉTHODE du SIMPLEXE n INTRODUCTION développée initialement par George Dantzig en 1947 n seule méthode exacte pour résoudre des problèmes linéaires de grande taille n méthode itérative algébrique où l’on circule séquentiellement sur les sommets à l’intérieur de la zone de solution jusqu’à l’obtention de la solution optimale n

MÉTHODE du SIMPLEXE : DÉFINITIONS n n n Systèmes d’équations équivalents n Systèmes qui possèdent le même ensemble de solutions Variable de base n Variable qui a un coefficient unitaire positif dans une des équations du système et un coefficient nul partout ailleurs Opérations pivot n Opération de Gauss-Jordan pour transformer un système d’équations équivalent dans lequel une variable devient de base Système canonique n Système d’équations où il y a une variable de base par équation Solution de base n Système d’équations où les variables hors base sont fixées à zéro résolu pour les variables de base

FORME NORMALISÉE n PROBLÈME de MAXIMISATION

SIMPLEXE, FORME MATRICIELLE

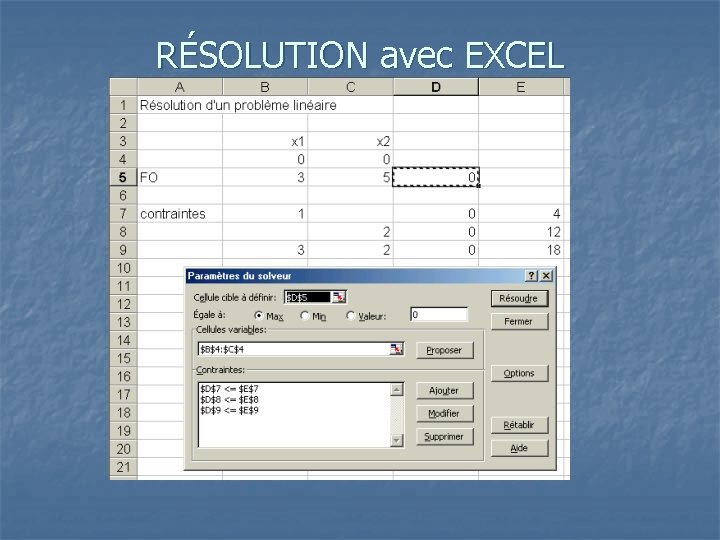
RÉSOLUTION avec EXCEL