Max Sea International Software editor for marine market

Max. Sea International Software editor for marine market Max. Sea is distributed in 25 countries Available in 13 languages. 90. 000 ships equiped

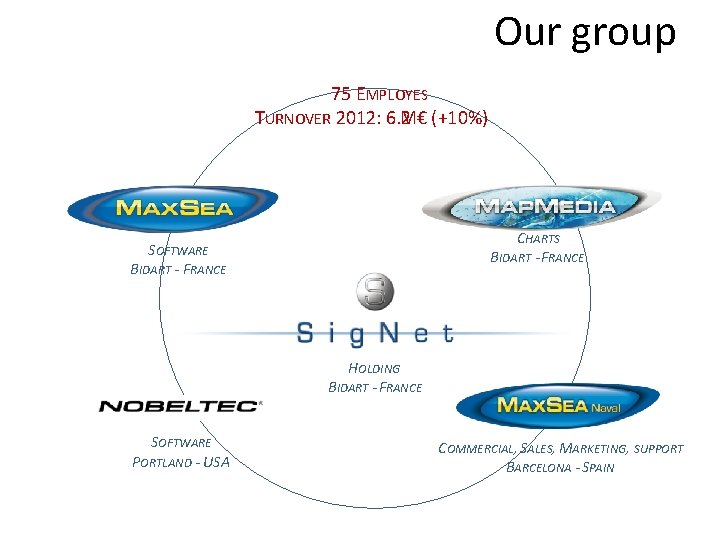
Our group 75 EMPLOYES TURNOVER 2012: 6. 2 M€ (+10%) CHARTS BIDART - FRANCE SOFTWARE BIDART - FRANCE HOLDING BIDART - FRANCE SOFTWARE PORTLAND - USA COMMERCIAL, SALES, MARKETING, SUPPORT BARCELONA - SPAIN

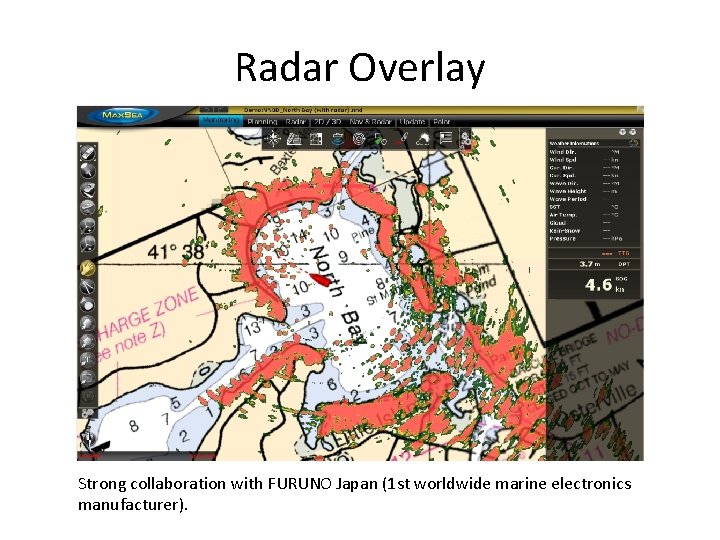
Radar Overlay Strong collaboration with FURUNO Japan (1 st worldwide marine electronics manufacturer).

Cameras FLIR (IR, night vision…)

Isochrones for minimum time route optimization • • • Wind polar Wave polar Set sail Weather prediction (wind, waves) Currents • Optimal route

DEMO

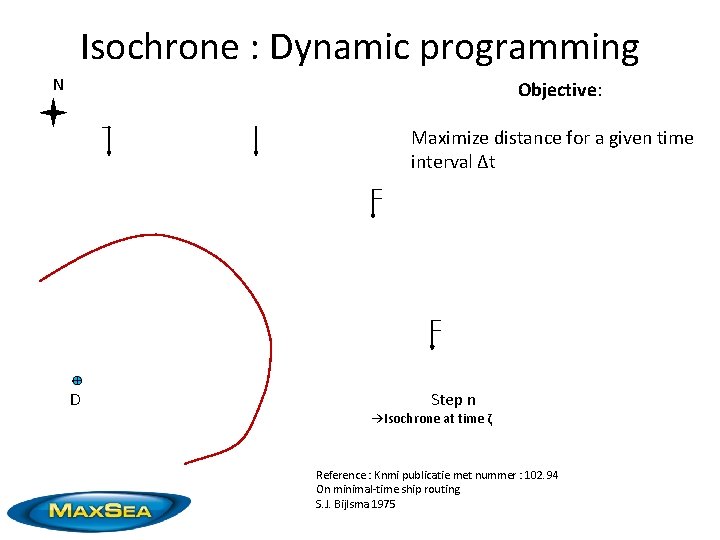
Isochrone : Dynamic programming N Objective: Maximize distance for a given time interval ∆t D Step n →Isochrone at time ζ Reference : Knmi publicatie met nummer : 102. 94 On minimal-time ship routing S. J. Bijlsma 1975

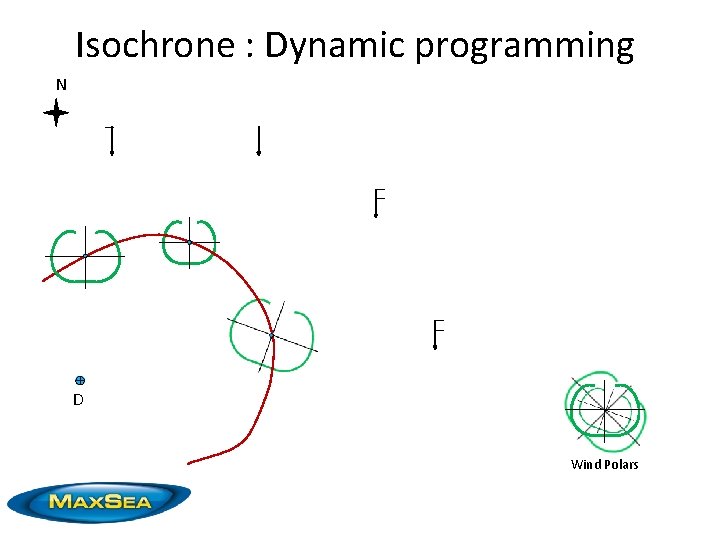
Isochrone : Dynamic programming N D Wind Polars

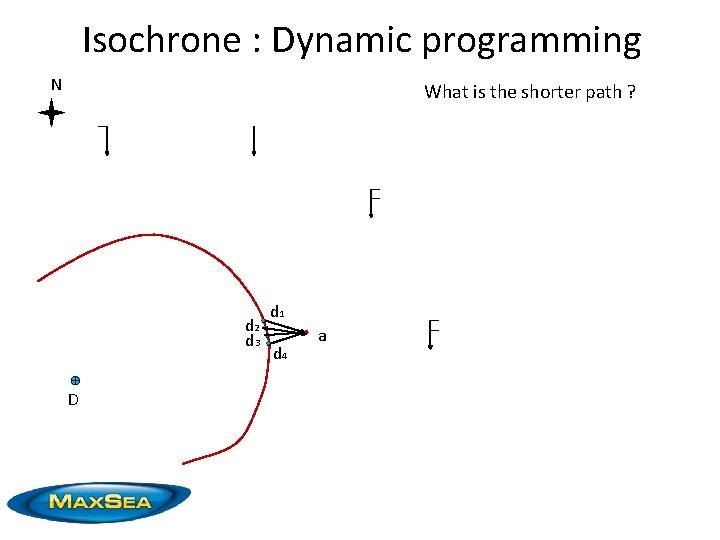
Isochrone : Dynamic programming N What is the shorter path ? d 2 d 3 D d 1 d 4 a

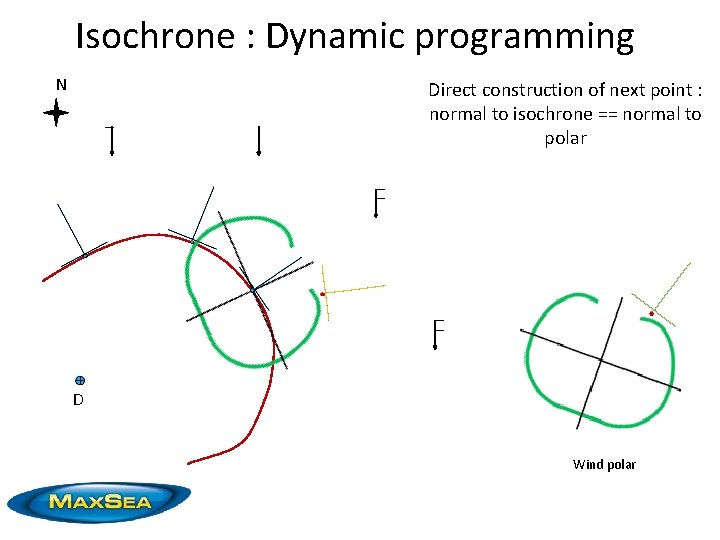
Isochrone : Dynamic programming N Direct construction of next point : normal to isochrone == normal to polar D Wind polar

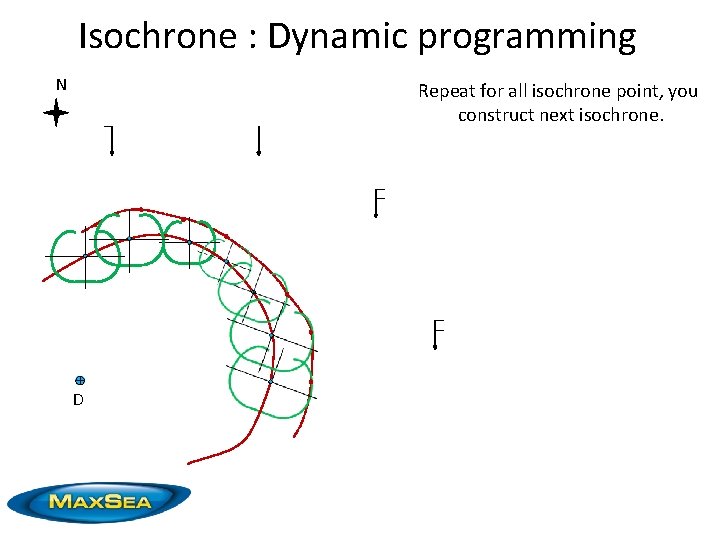
Isochrone : Dynamic programming N Repeat for all isochrone point, you construct next isochrone. D

Isochrone : Dynamic programming Next isochrone (dash) Optimization becomes a geometrical optimization. Not easy to resolve, in good computational time, taking into account numerical precision. Multiple path for optimal route at intersection point.

Route optimization for motor boats • Main goal: fuel consumption optimization. But also limit weather conditions. • Several types of boats – Motor with sail assistance – Motor Sailing – Sailing

3 D Routing • New problem : find best course (2 d) and best motor speed (power) to minimize fuel consumption. • Motor and Motor. Sail boats have round speed polars (motor always on) => isochrones are isodistance (shortest path).

Fuel Consumption models • Motor : – Hydro & areo dynamic forces + motor consumption curve. – Approximation 2 nd degree from speed inside speed limits (18 -25 kts) : Conso t/nm = 0. 0036*V 2 + 0. 1015 V + 0. 8848 (not linear) • Motor Sailing : mutilple Wind polar curves (for each motor power / sail %).

Fast Marching Method Ordered Upwind Method • We wanted a new method for 2 D & 3 D (more easy to implement than 3 D geometric calculation). • Differential equation : Consumption = f(x, y, t, course, motor power). • Front propagation. • Strong anisotropy : wind and wind polar (sailing) or waves.

Ordered Upwind Method Considered are sorted according to cost. Reference : SIAM J. Numer. Anal. , 41(1), 325– 363. (39 pages) Ordered Upwind Methods for Static Hamilton--Jacobi Equations: Theory and Algorithms

Ordered Upwind Method Smallest Considered is removed from Sorted Queue. It becomes the Last Accepted.

Ordered Upwind Method All Neighbors of Last Accepted are updated. Cost and Arrival Time are computed.

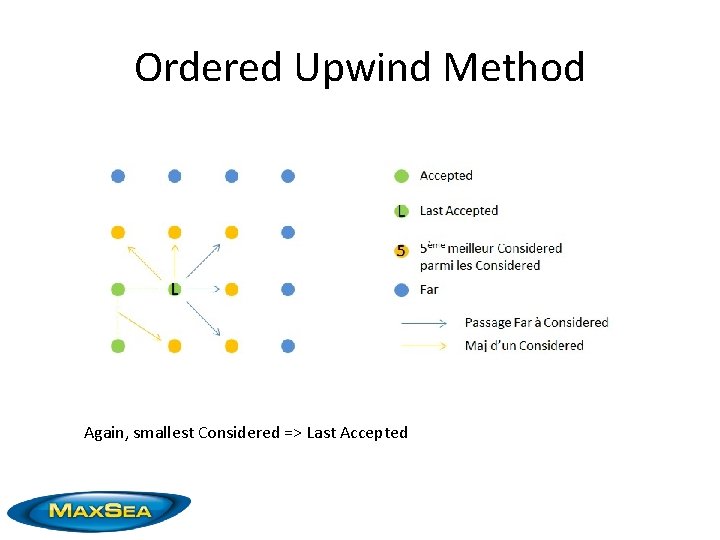
Ordered Upwind Method Again, smallest Considered => Last Accepted

Ordered Upwind Method The Front advanced with 2 new Accepted. Loop until arrival point is reached.

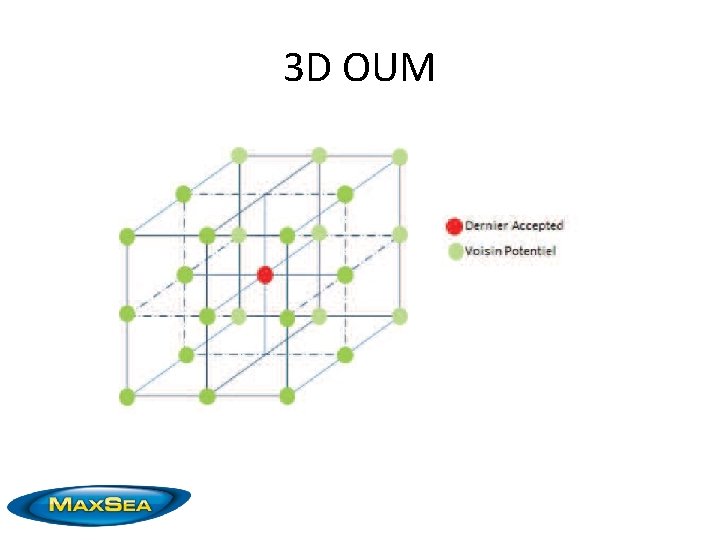
3 D OUM

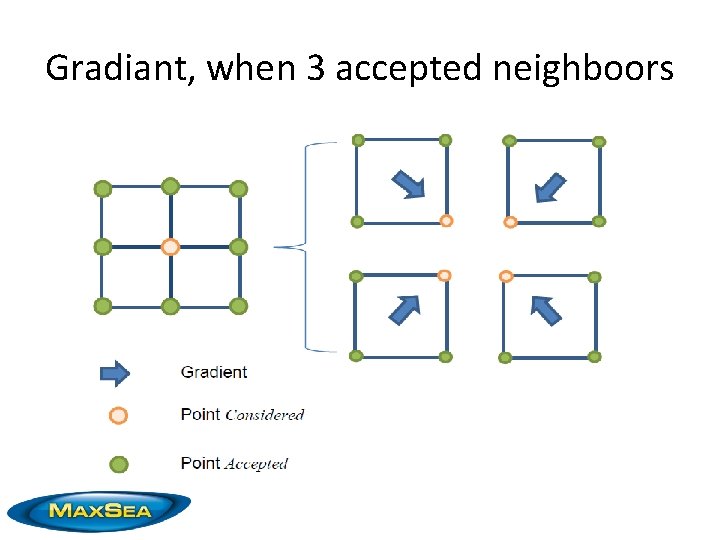
OUM : 3 update methods • Direct Cost : from a node to horizontal, vertical or diagonal node. • Enumeration : minimise over 20 angles (original method from Vladimirsky) • Gradiant : from downwind gradiant, select best speed vector in polar, use it to compute upwind.

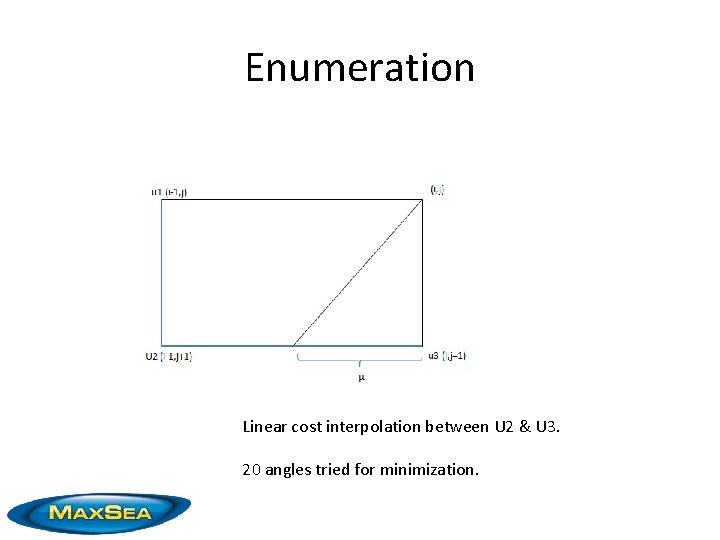
Enumeration Linear cost interpolation between U 2 & U 3. 20 angles tried for minimization.

Gradiant, when 3 accepted neighboors

DEMO

Experience • Difficult to validate results : reference solution. • Gradiant was working during unit testing, we found problems during integration. • Parallel algorithm is not evidence. • Software optimization is needed for interactive simulations.