Max Flow min Cut Max FlowMin Cut Problem

Max Flow min Cut

Max Flow/Min Cut
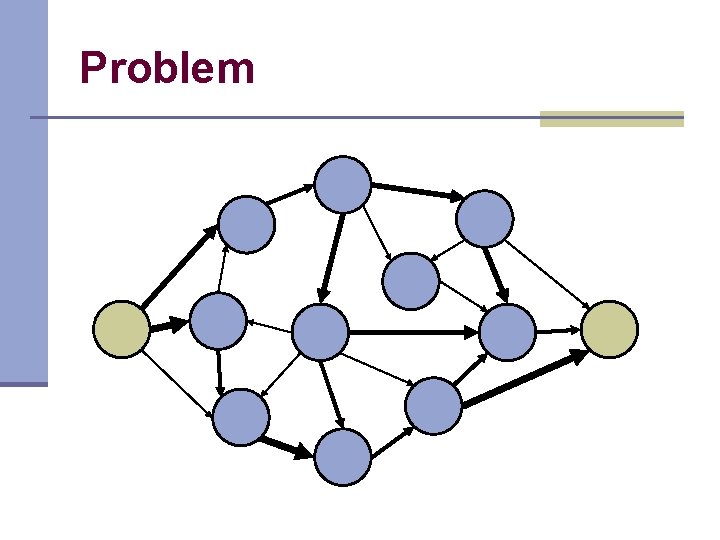
Problem
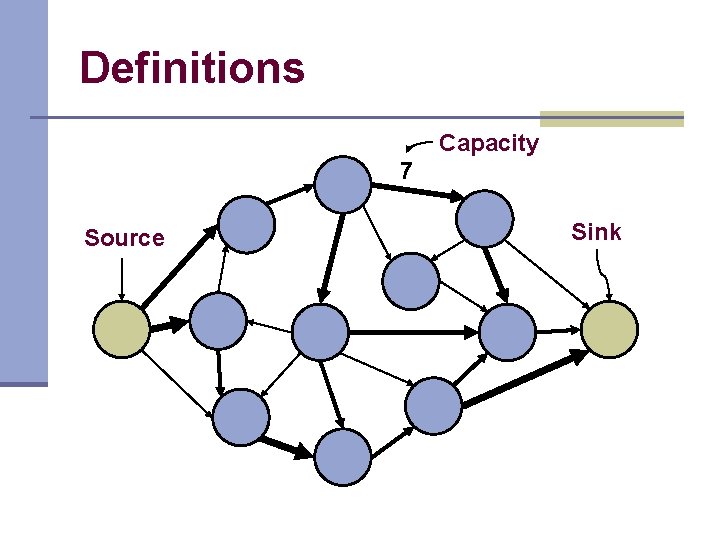
Definitions Capacity 7 Source Sink
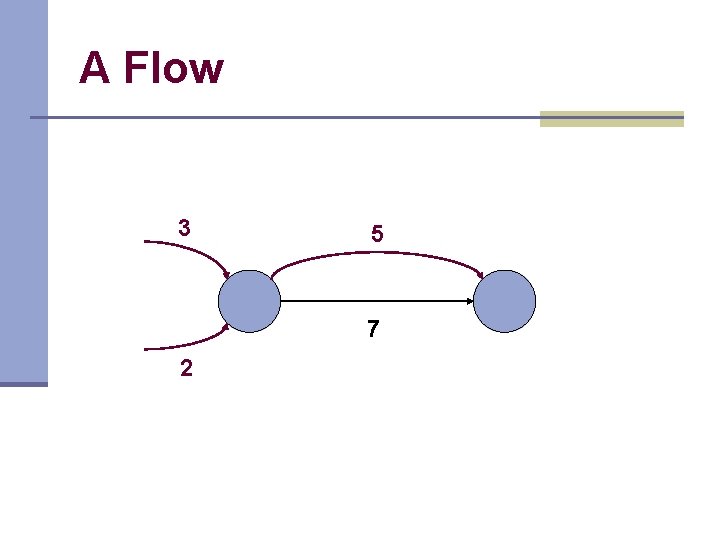
A Flow 3 5 7 2
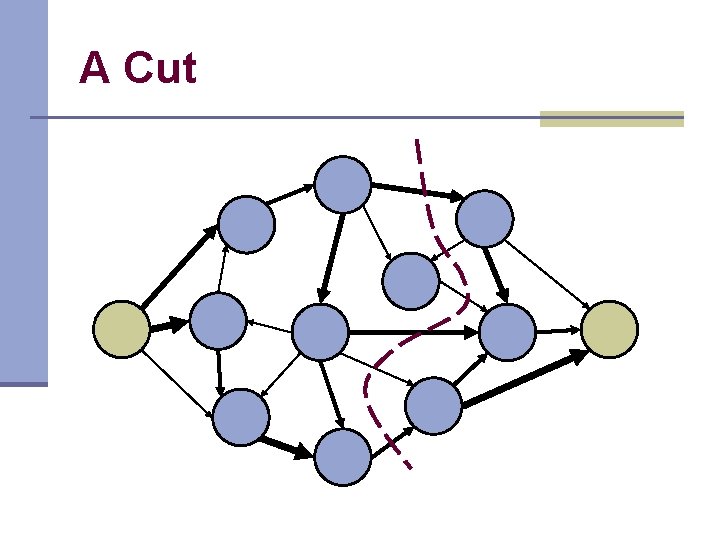
A Cut
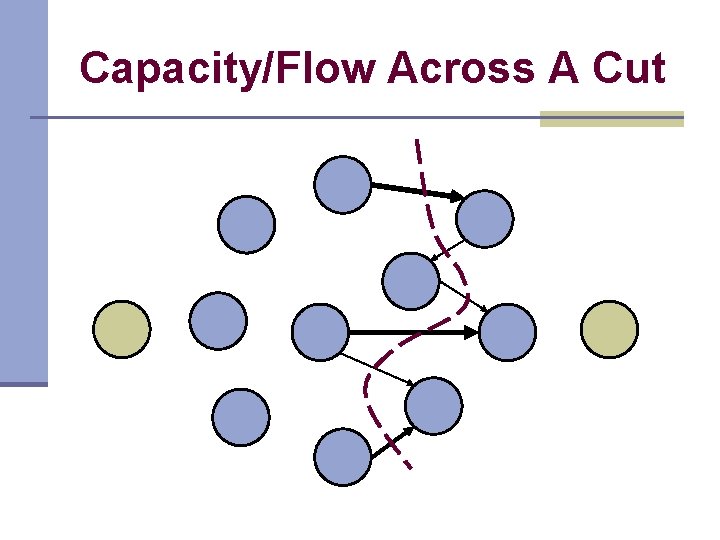
Capacity/Flow Across A Cut

Problem n Find a cut with minimum capacity n Find maximum flow from source to sink
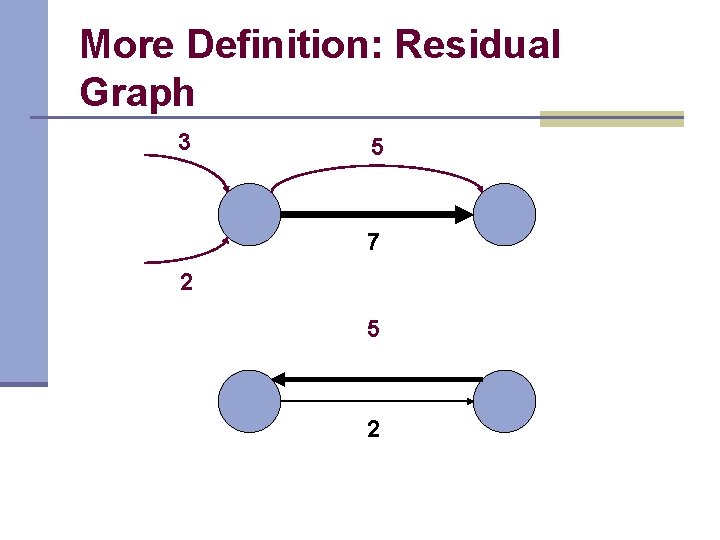
More Definition: Residual Graph 3 5 7 2 5 2

Augmenting Path n A path from source to sink in the residual graph of a given flow

Idea n If there is an augmenting path in the residual graph, we can push more flow

Ford-Fulkerson Method initialize total flow to 0 residual graph G’= G while augmenting path exist in G’ pick a augmenting path P in G’ m = bottleneck capacity of P add m to total flow push flow of m along P update G’
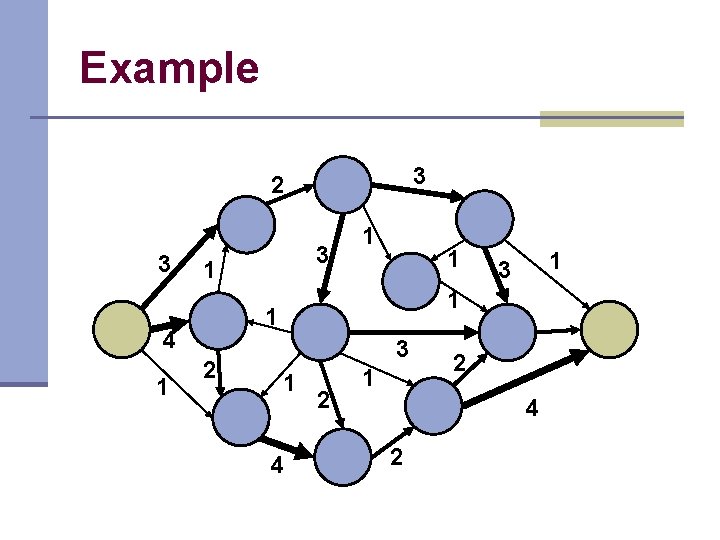
Example 3 2 3 1 1 2 1 3 1 1 4 1 3 1 4 2 1 2 4 2
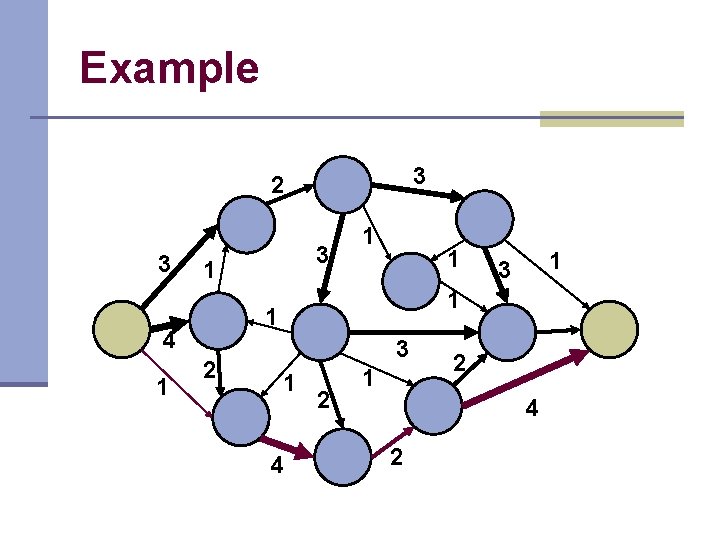
Example 3 2 3 1 1 2 1 3 1 1 4 1 3 1 4 2 1 2 4 2
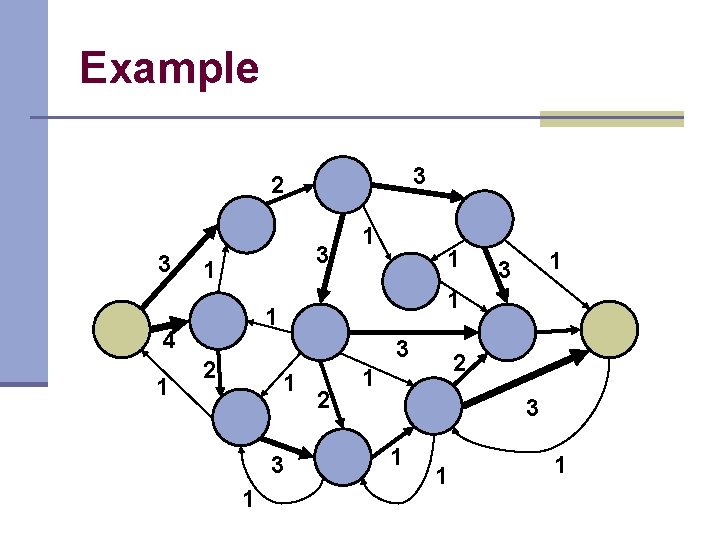
Example 3 2 3 3 1 1 3 2 1 3 1 1 4 1 1 2 2 1 3 1 1 1
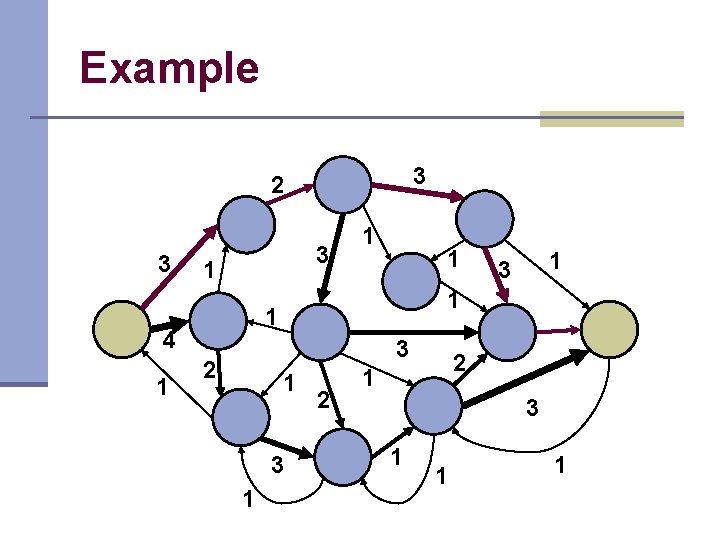
Example 3 2 3 3 1 1 3 2 1 3 1 1 4 1 1 2 2 1 3 1 1 1
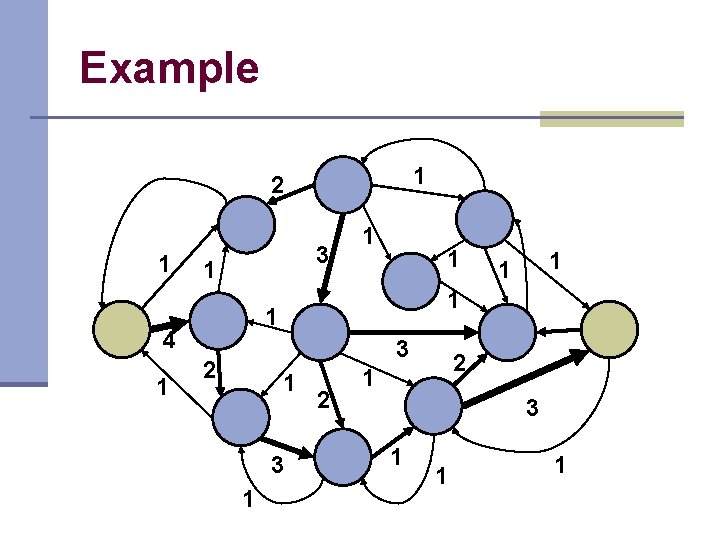
Example 1 2 1 3 1 1 3 2 1 3 1 1 1 4 1 1 2 2 1 3 1 1 1
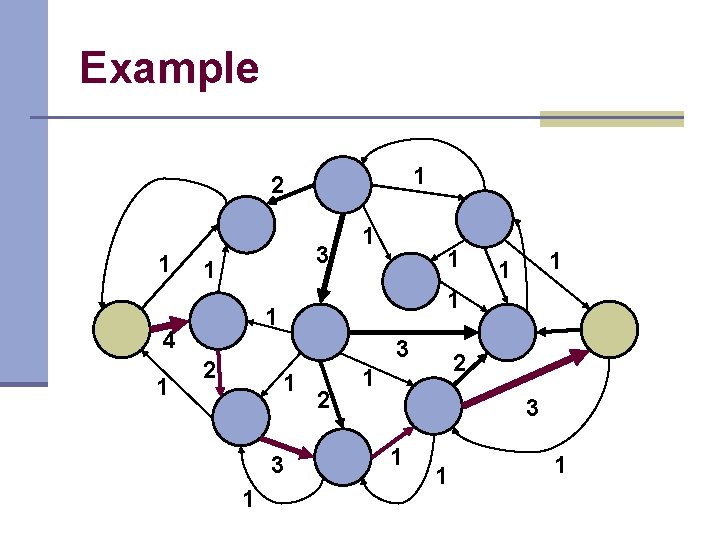
Example 1 2 1 3 1 1 3 2 1 3 1 1 1 4 1 1 2 2 1 3 1 1 1
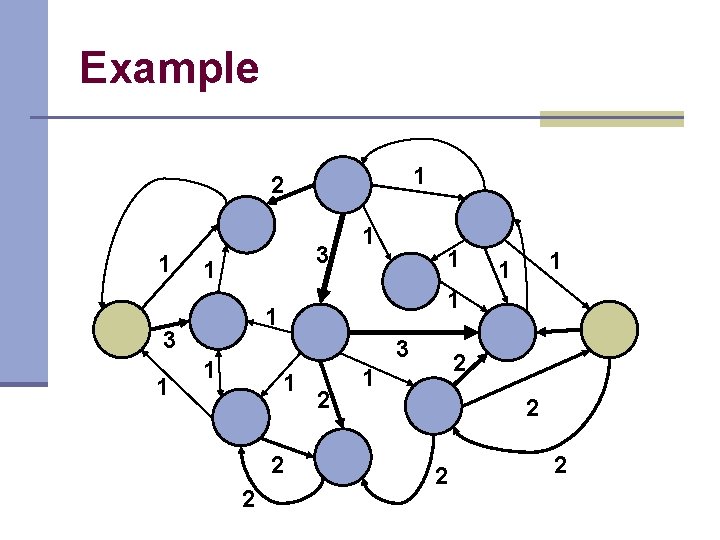
Example 1 2 1 3 1 1 2 2 1 1 3 1 1 2 2 2
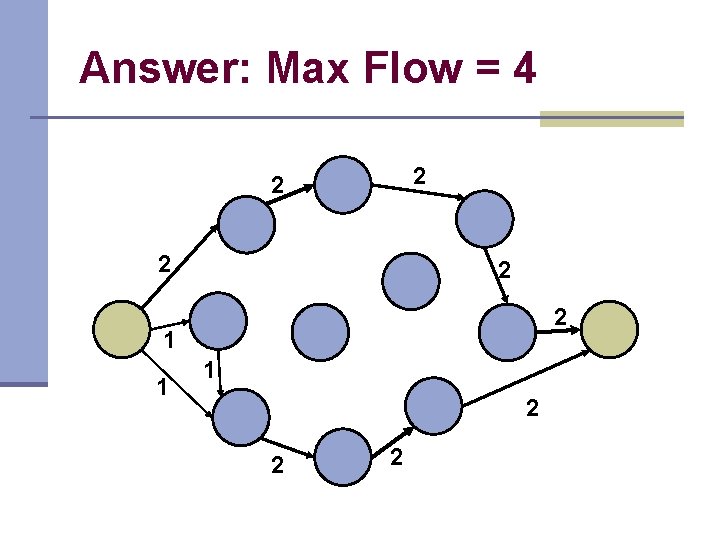
Answer: Max Flow = 4 2 2 2 1 1 1 2 2 2
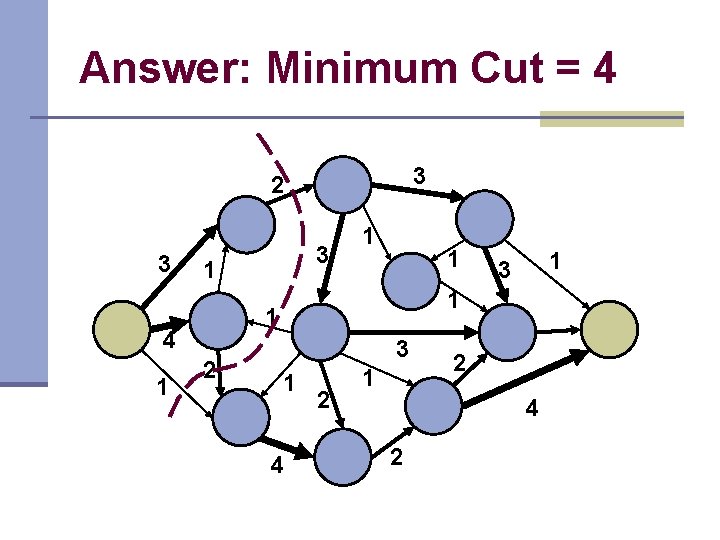
Answer: Minimum Cut = 4 3 2 3 1 1 2 1 3 1 1 4 1 3 1 4 2 1 2 4 2

Find Augmenting Path? initialize total flow to 0 residual graph G’= G while augmenting path exist in G’ pick a augmenting path P in G’ m = bottleneck capacity of P add m to total flow push flow of m along P update G’

Picking Augmenting Path Edmonds-Karp’s Heuristics n I. II. Find a path with maximum bottleneck capacity Find a path with minimum length

Variations n How about Maximum Cut?

Applications for Max. Flow/Min. Cut
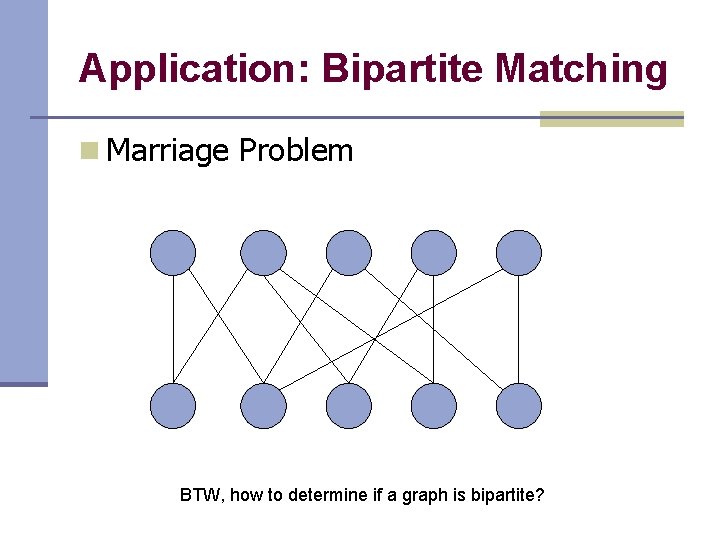
Application: Bipartite Matching n Marriage Problem BTW, how to determine if a graph is bipartite?
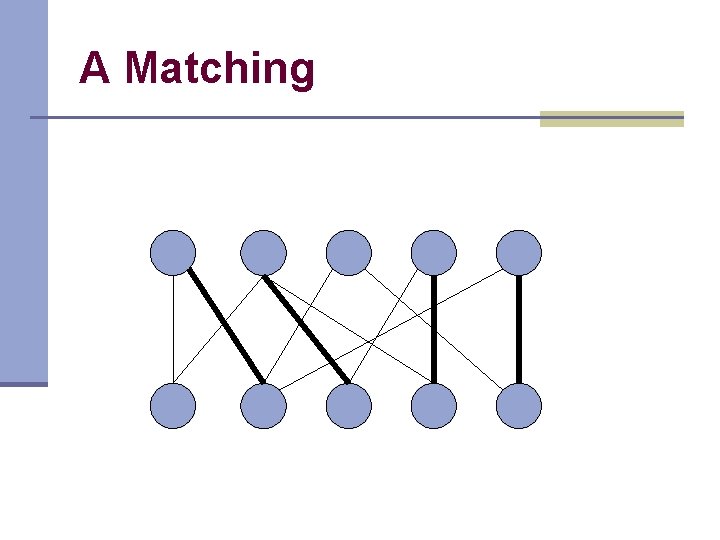
A Matching
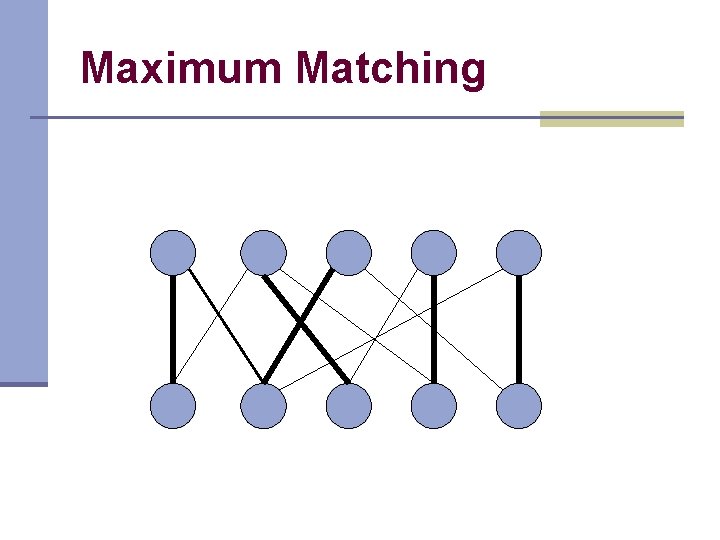
Maximum Matching
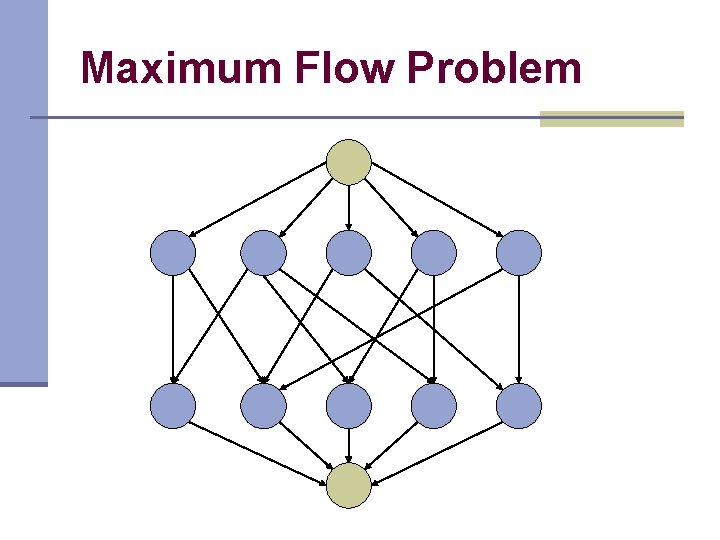
Maximum Flow Problem
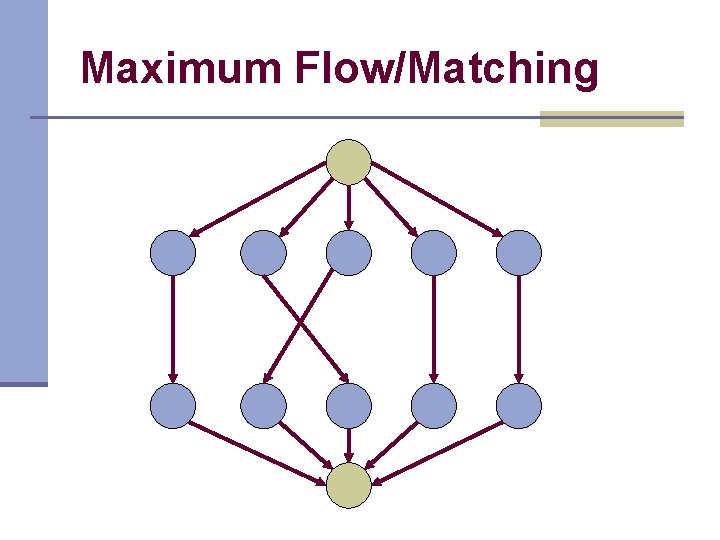
Maximum Flow/Matching
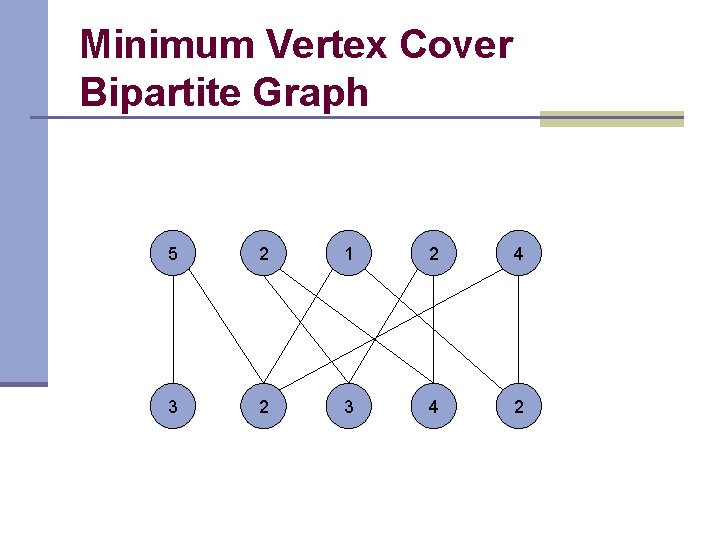
Minimum Vertex Cover Bipartite Graph 5 2 1 2 4 3 2 3 4 2
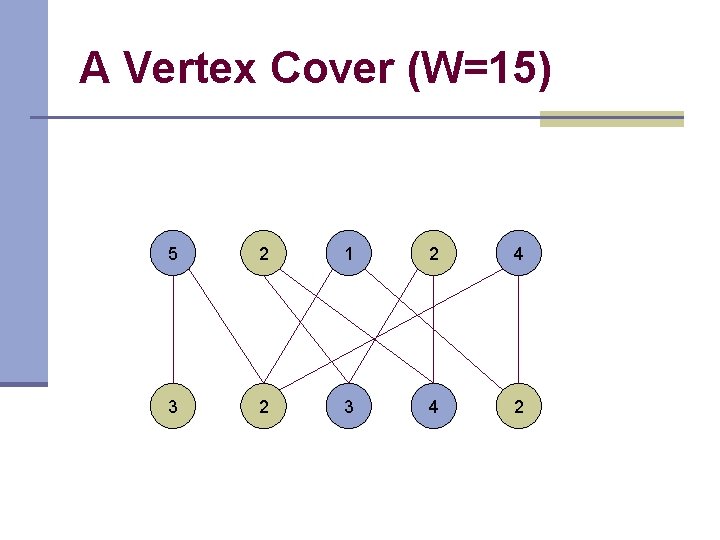
A Vertex Cover (W=15) 5 2 1 2 4 3 2 3 4 2
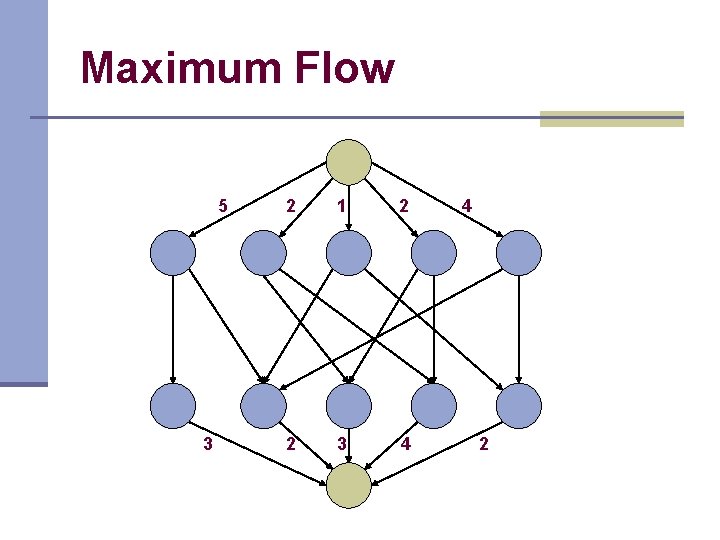
Maximum Flow 5 3 2 1 2 2 3 4 4 2
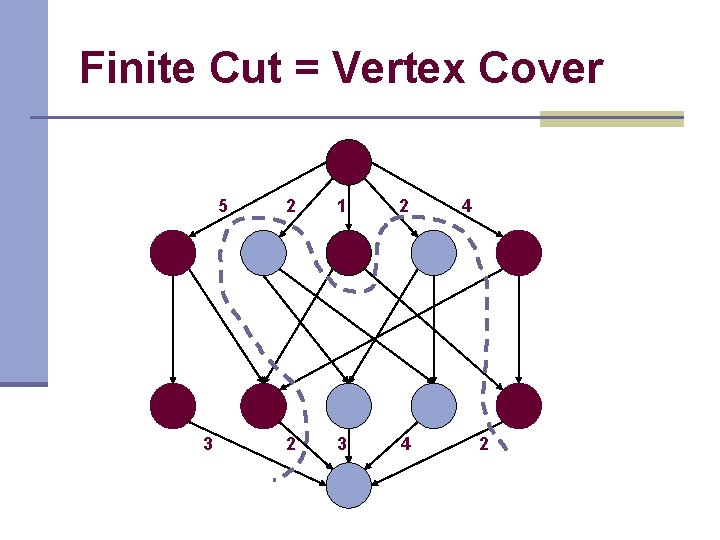
Finite Cut = Vertex Cover 5 3 2 1 2 2 3 4 4 2
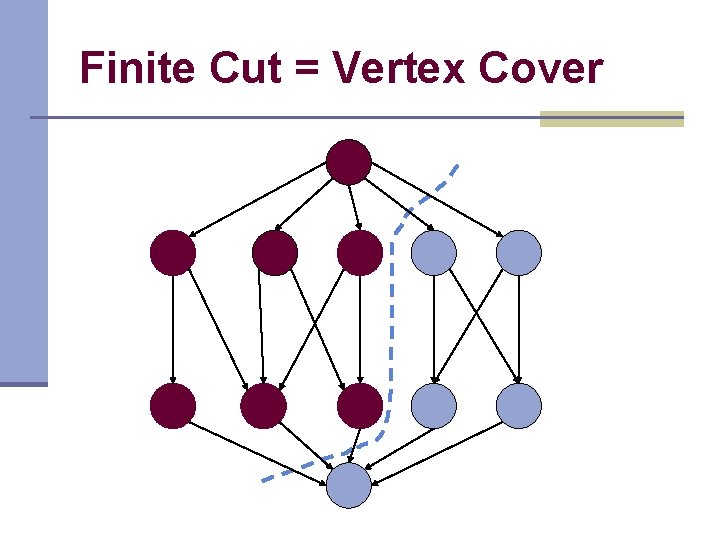
Finite Cut = Vertex Cover

Problems. .
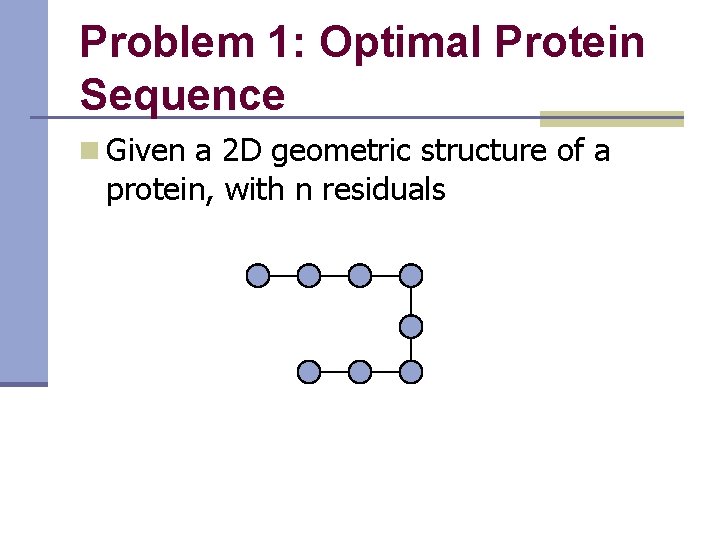
Problem 1: Optimal Protein Sequence n Given a 2 D geometric structure of a protein, with n residuals

Optimal Protein Sequence n Each residual can be either hydrophobic (H) or polar (P)

Optimal Sequence n Each residual has a “solvent area” n Want to reduce solvent areas of Hs n Want to increase pairs of Hs in close contacts

Optimal Sequence n Assign H, P to the residuals to minimize d(i, j): 1 if H at position i and H at position j is close enough, 0 otherwise s(i) : area exposed at position i
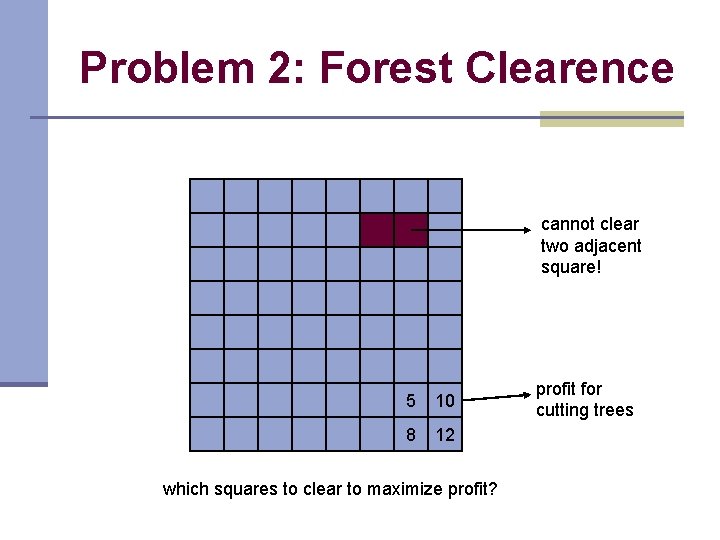
Problem 2: Forest Clearence cannot clear two adjacent square! 5 10 8 12 which squares to clear to maximize profit? profit for cutting trees

Problem 3: All-Pair Maximum Bottleneck Bandwidth Path n Given a graph, how to find the maximum bottleneck bandwidth path between any two nodes, u and v, efficiently?
- Slides: 42