Matura 2010 z matematyki na poziomie rozszerzonym PLANIMETRIA

Matura 2010 z matematyki na poziomie rozszerzonym

PLANIMETRIA

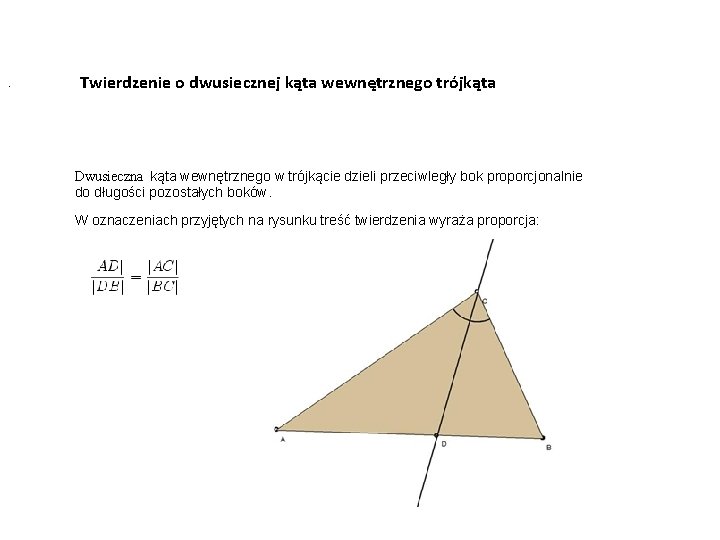
. Twierdzenie o dwusiecznej kąta wewnętrznego trójkąta Dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok proporcjonalnie do długości pozostałych boków. W oznaczeniach przyjętych na rysunku treść twierdzenia wyraża proporcja:

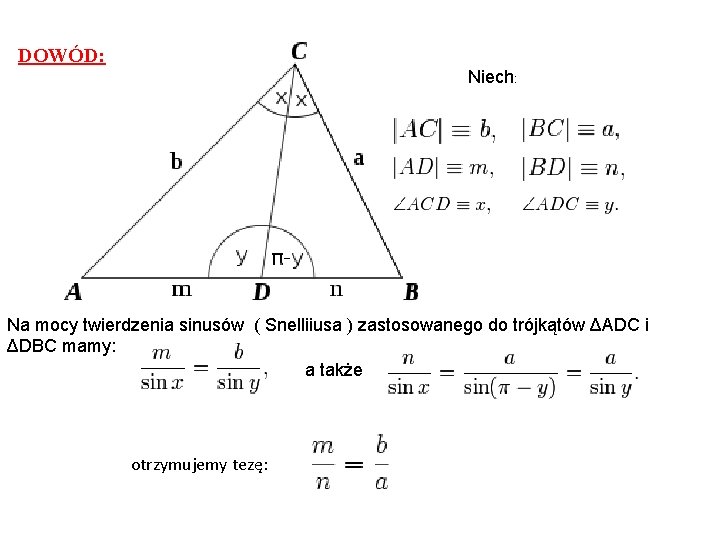
DOWÓD: Niech: Na mocy twierdzenia sinusów ( Snelliiusa ) zastosowanego do trójkątów ΔADC i ΔDBC mamy: a także otrzymujemy tezę:

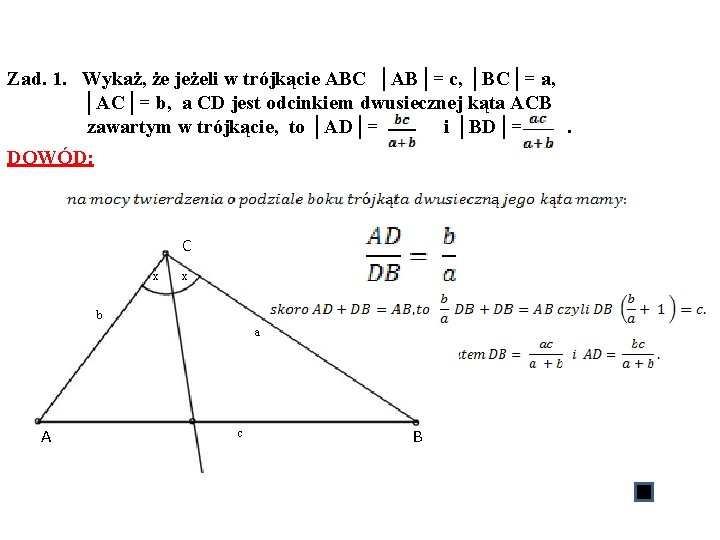
Zad. 1. Wykaż, że jeżeli w trójkącie ABC │AB│= c, │BC│= a, │AC│= b, a CD jest odcinkiem dwusiecznej kąta ACB zawartym w trójkącie, to │AD│= i │BD│=. DOWÓD: C x x b a A D c B

Zad. 2. W trójkącie prostokątnym przyprostokątne mają długość a i b. Oblicz długość odcinków na jakie dzieli przeciwprostokątną dwusieczna kąta prostego. DOWÓD: B D a C b A

Zad. 3. DOWÓD: W trójkącie ABC │BC│= a, │AC│= b oraz │CD│= d, gdzie CD jest odcinkiem leżącym na dwusiecznej kąta ACB zawartym w trójkącie. Oblicz długość boku │AB│ tego trójkąta.

Zad. 4. Wykaż, że jeżeli suma długości wysokości trójkąta jest 9 razy większa od długości promienia okręgu wpisanego w ten trójkąt, to trójkąt jest równoboczny. DOWÓD:

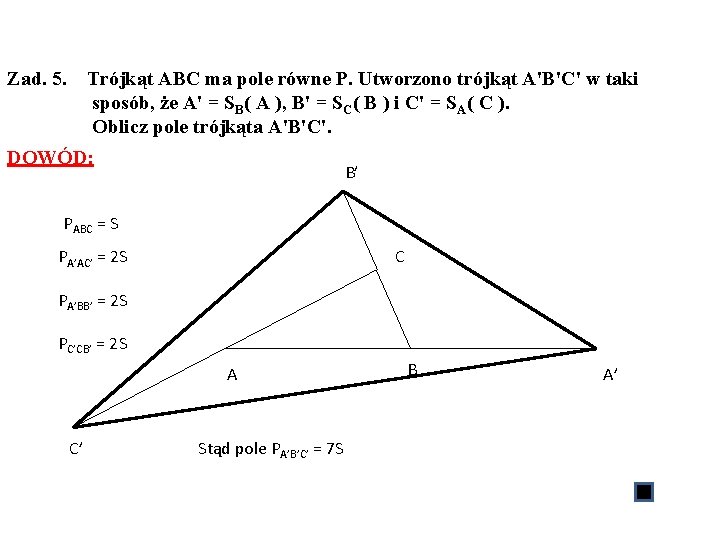
Zad. 5. Trójkąt ABC ma pole równe P. Utworzono trójkąt A'B'C' w taki sposób, że A' = SB( A ), B' = SC( B ) i C' = SA( C ). Oblicz pole trójkąta A'B'C'. DOWÓD: B’ PABC = S C PA’AC’ = 2 S PA’BB’ = 2 S PC’CB’ = 2 S A C’ Stąd pole PA’B’C’ = 7 S B A’

Zad. 6. DOWÓD: W trójkącie poprowadzono środkowe boków. Podzieliły one trójkąt na sześć mniejszych trójkątów. Wykaż, że pola powstałych trójkątów są równe.

Zad. 7. DOWÓD: Wykaż, że okrąg wpisany w trójkąt prostokątny jest styczny do przeciwprostokątnej w punkcie dzielącym ją na dwa odcinki, których iloczyn długości jest równy polu tego trójkąta.

Zad. 8. Wyznacz długość boku c trójkąta, jeśli dane są długości a i b boków trójkąta oraz wiadomo, że ha + hb = hc, gdzie ha, hb, hc są długościami wysokości opuszczonych na odpowiednie boki DOWÓD: trójkąta.

Zad. 9. DOWÓD: Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają zależność , to trójkąt ten jest równoramienny.

Zad. 10. Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem DOWÓD: równobocznym.

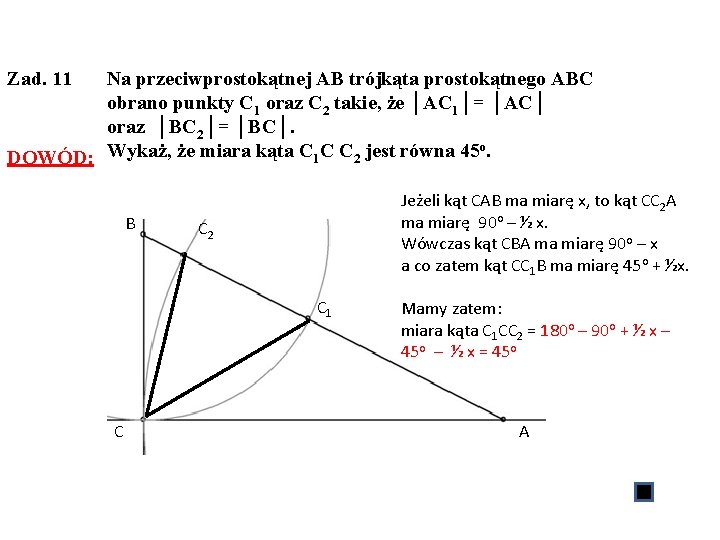
Zad. 11 Na przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punkty C 1 oraz C 2 takie, że │AC 1│= │AC│ oraz │BC 2│= │BC│. o DOWÓD: Wykaż, że miara kąta C 1 C C 2 jest równa 45. B Jeżeli kąt CAB ma miarę x, to kąt CC 2 A ma miarę 90 o – ½ x. Wówczas kąt CBA ma miarę 90 o – x a co zatem kąt CC 1 B ma miarę 45 o + ½x. C 2 C 1 C Mamy zatem: miara kąta C 1 CC 2 = 180 o – 90 o + ½ x – 45 o – ½ x = 45 o A

LICZBY RZECZYWISTE

Zad. 1. Wykaż, że dla dowolnych liczb rzeczywistych a, b zachodzi nierówność: a 2 + b 2 + 2 2 ( a + b ) DOWÓD: Mamy pokazać, że a 2 + b 2 + 2 2 ( a + b ) ale a 2 + b 2 + 2 2 a + 2 b a 2 – 2 a + b 2 – 2 b + 2 0 a 2 – 2 a + 1 + b 2 – 2 b + 1 0 ( a – 1 )2 + ( b – 1 ) 2 0

Zad. 2. Wykaż, że liczba 318 – 218 jest liczbą podzielną przez 19. DOWÓD: 318 – 218 = ( 39 – 29 )(39 + 29 ) = =(33 – 23 )( 36 + 33 33 + 26 )(39 + 29 ) = =19 (36 + 33 33 + 26 )(39 + 29 )

Zad. 3. Udowodnij, że trzy liczby a, b, c tworzące ciąg geometryczny spełniają warunek: ( a + b + c )( a – b + c ) = a 2 + b 2 + c 2, DOWÓD: Dane są liczby; a, b = aq, c = aq 2 wówczas ( a + b + c )( a – b + c ) = a 2 (1 + q 2 )( 1 – q + q 2 ) = = a 2 (1 – q + q 2 + q – q 2 + q 3 + q 2 – q 3 + q 4 ) = = a 2 (1 + q 2 + q 4 ) = a 2 + a 2 q 4 = a 2 + b 2 + c 2

Zad. 4. DOWÓD: Udowodnij, że w ciągu geometrycznym o parzystej liczbie wyrazów stosunek sumy wyrazów stojących na miejscach parzystych do sumy wyrazów stojących na miejscach nieparzystych jest równy ilorazowi tego ciągu.

Zad. 5. Udowodnij, że jeśli różne liczby a 2, b 2, c 2 tworzą ciąg arytmetyczny, to liczby też tworzą ciąg arytmetyczny. DOWÓD:

Zad. 6. Wykaż, że: gdzie a b, b c i a c DOWÓD: