Matthias Kawski On Agrachevs curvature of optimal control

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 On Agrachev’s curvature of optimal control Matthias Kawski Eric Gehrig Arizona State University Tempe, U. S. A. This work was partially supported by NSF grant DMS 00 -72369. http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Outline • Motivation. WANTED: Sufficient conditions for optimality • Review / survey: – Agrachev’s definition and main theorem – Comment: connection to recent work on Dubins’ car (Chitour, Sigalotti) – Best studied case: Zermelo’s navigation problem (Ulysse Serres) • Computational issues, – Computer Algebra Systems. Live interactive? • Recent efforts to “visualize” curvature of optimal control – how to read our pictures – what one may be able to see in our pictures • Conclusion / outlook / current work: – Connection with Bang-Bang controls. Relaxation/ approximation, http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 References • A. Agrachev: On the curvature of control systems (abstract, SISSA 2000) • A. Agrachev and Yu. Sachkov: Lectures on Geometric Control Theory (SISSA 2001) Control Theory from the Geometric Viewpoint (Springer 2004) • Ulysse Serres, The curvature of 2 -dimensional optimal control systems' and Zermelo’s navigation problem. (preprint 2002). • A. Agrachev, N. Chtcherbakova, and I. Zelenko, On curvatures and focal points of dynamical Lagrangian distributions and their reductions by 1 st integrals (preprint 2004) • M. Sigalotti and Y. Chitour, Dubins' problem on surfaces. II. Nonpositive curvature (preprint 2004) On the controllability of the Dubins problem for surfaces (preprint 2004) http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Purpose/use of curvature in opt. control Maximum principle provides comparatively straightforward necessary conditions for optimality, sufficient conditions are in general harder to come by, and often comparatively harder to apply. Curvature (w/ corresponding comparison theorem) suggest an elegant geometric alternative to obtain verifiable sufficient conditions for optimality compare classical Riemannian geometry http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Curvature of optimal control • understand the geometry (very briefly) • develop intuition in basic examples • apply to obtain new optimality results http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Curvature and double-Lie-brackets • Usually, we think of curvature as defined in terms of connections e. g. • But here it is convenient to think of curvature as a measure of the lack of integrability of a “horizontal distribution” of horizontal lifts. In the case of a 2 -dimensional base manifold, let g be the “unit” vertical field of “infinitesimal rotation in fibres”, and f be the geodesic vector field. In this case Gauss curvature is obtained as: Recent beautiful application, analysis and controllability results by Chitour & Sigalotti for control of “Dubins car on curved surfaces”. http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Curvature of optimal control • understand the geometry • develop intuition in basic examples • apply to obtain new optimality results http: //math. asu. edu/~kawski@asu. edu

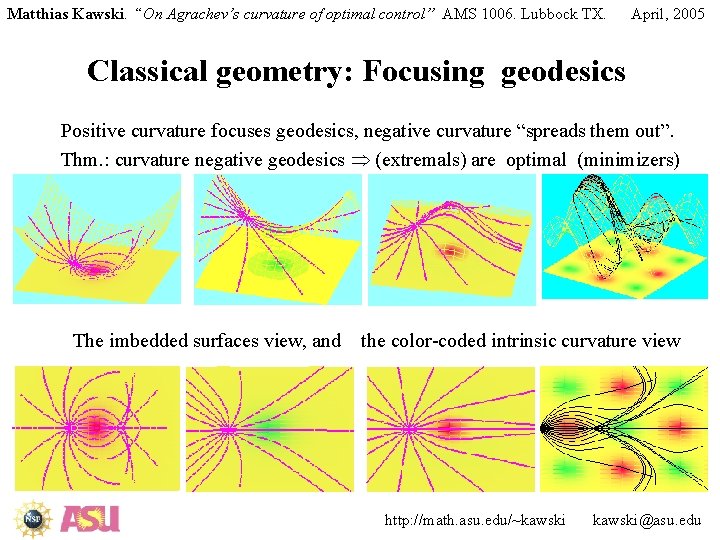
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Classical geometry: Focusing geodesics Positive curvature focuses geodesics, negative curvature “spreads them out”. Thm. : curvature negative geodesics (extremals) are optimal (minimizers) The imbedded surfaces view, and the color-coded intrinsic curvature view http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Definition versus formula A most simple geometric definition - beautiful and elegant. but the formula in coordinates is incomprehensible (compare classical curvature…) (formula from Ulysse Serres, 2001) http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. http: //math. asu. edu/~kawski April, 2005 kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Aside: other interests / plans • What is theoretically /practically feasible to compute w/ reasonable resources? (e. g. CAS: “simplify”, old: “controllability is NP-hard”, MK 1991) • Interactive visualization in only your browser… – “CAS-light” inside JAVA (e. g. set up geodesic eqns) – “real-time” computation of geodesic spheres (e. g. “drag” initial point w/ mouse, or continuously vary parameters…) Riemannian, circular parabloid “bait”, “hook”, like Mandelbrot fractals…. http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 From: Agrachev / Sachkov: “Lectures on Geometric Control Theory”, 2001 http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 From: Agrachev / Sachkov: “Lectures on Geometric Control Theory”, 2001 http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 From: Agrachev / Sachkov: “Lectures on Geometric Control Theory”, 2001 Next: Define distinguished parameterization of H x http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 The canonical vertical field v http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Jacobi equation in moving frame Frame or: http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Zermelo’s navigation problem “Zermelo’s navigation formula” http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 formula for curvature ? total of 782 (279) terms in num, 23 (7) in denom. MAPLE can’t factor… http: //math. asu. edu/~kawski@asu. edu

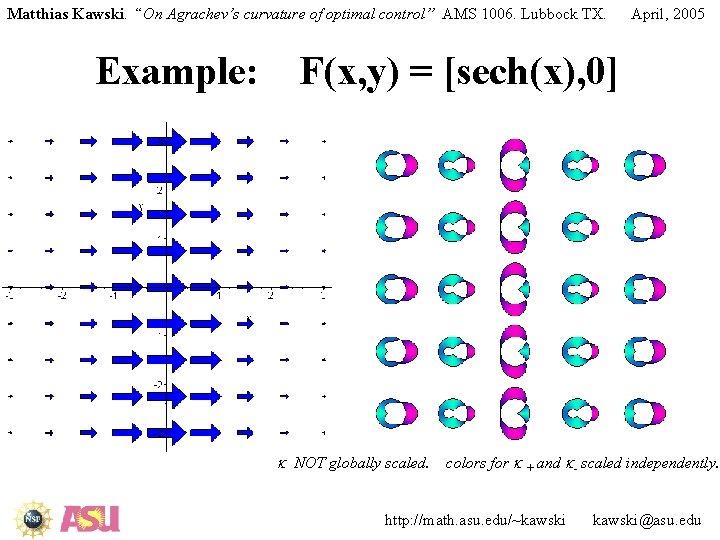
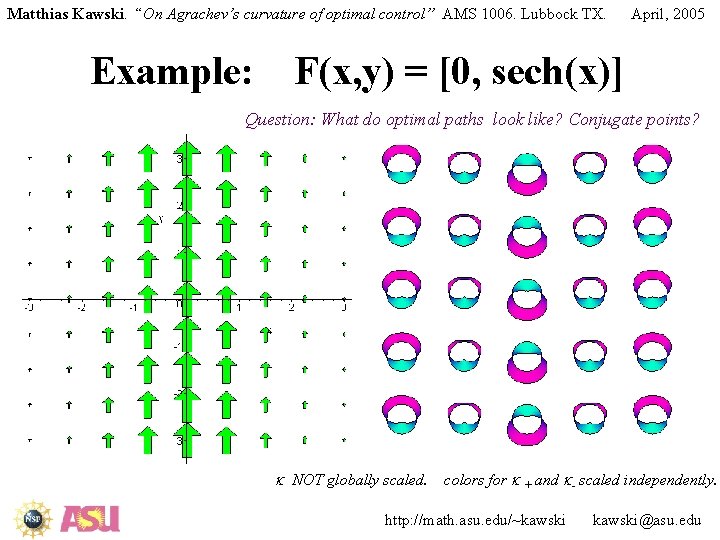
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 First pictures: fields of polar plots • On the left: the drift-vector field (“wind”) • On the right: field of polar plots of k(x 1, x 2, f) in Zermelo’s problem u* = f. (polar coord on fibre) polar plots normalized and color enhanced: unit circle zero curvature negative curvature inside greenish positive curvature outside pinkish http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. Example: April, 2005 F(x, y) = [sech(x), 0] k NOT globally scaled. colors for k + and k- scaled independently. http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. Example: April, 2005 F(x, y) = [0, sech(x)] Question: What do optimal paths look like? Conjugate points? k NOT globally scaled. colors for k + and k- scaled independently. http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Special case: linear drift • linear drift F(x)=Ax, i. e. , (dx/dt)=Ax+eiu • Curvature is independent of the base point x, study dependence on parameters of the drift k. A(x 1, x 2, f) = k(f, A) This case was studied in detail by U. Serres. Here we only give a small taste of the richness of even this very special simple class of systems http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Linear drift, preparation I • (as expected), curvature commutes with rotations quick CAS check: > k['B']: =combine(simplify(zerm(Bxy, x, y, theta), trig)); http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Linear drift, preparation II • (as expected), curvature scales with eigenvalues (homogeneous of deg 2 in space of eigenvalues) quick CAS check: > kdiag: =zerm(lambda*x, mu*y, x, y, theta); Note: q is even and also depends only on even harmonics of q http: //math. asu. edu/~kawski@asu. edu

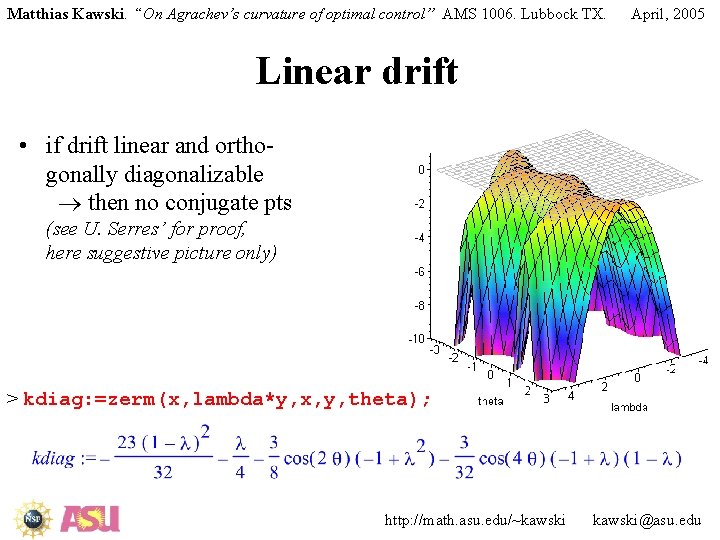
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Linear drift • if drift linear and orthogonally diagonalizable then no conjugate pts (see U. Serres’ for proof, here suggestive picture only) > kdiag: =zerm(x, lambda*y, x, y, theta); http: //math. asu. edu/~kawski@asu. edu

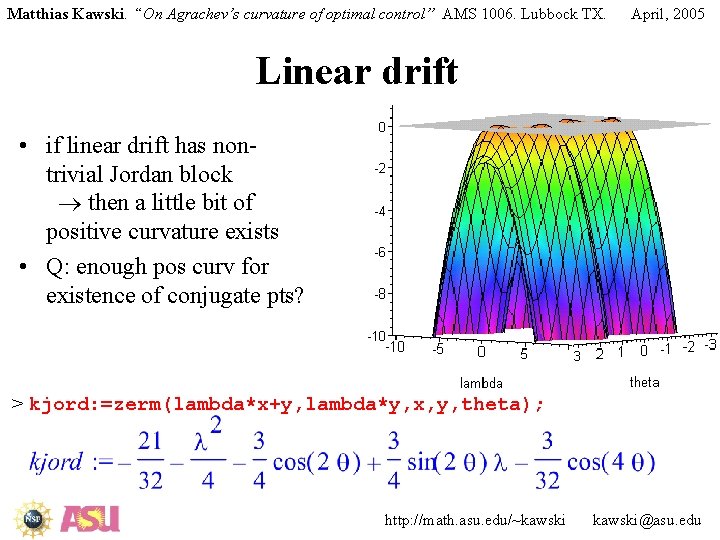
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Linear drift • if linear drift has nontrivial Jordan block then a little bit of positive curvature exists • Q: enough pos curv for existence of conjugate pts? > kjord: =zerm(lambda*x+y, lambda*y, x, y, theta); http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Some linear drifts diag w/ l=10, -1 Question: Which case is good for optimal control? diag w/ l=1+i, 1 -i jordan w/ l=13/12 http: //math. asu. edu/~kawski@asu. edu

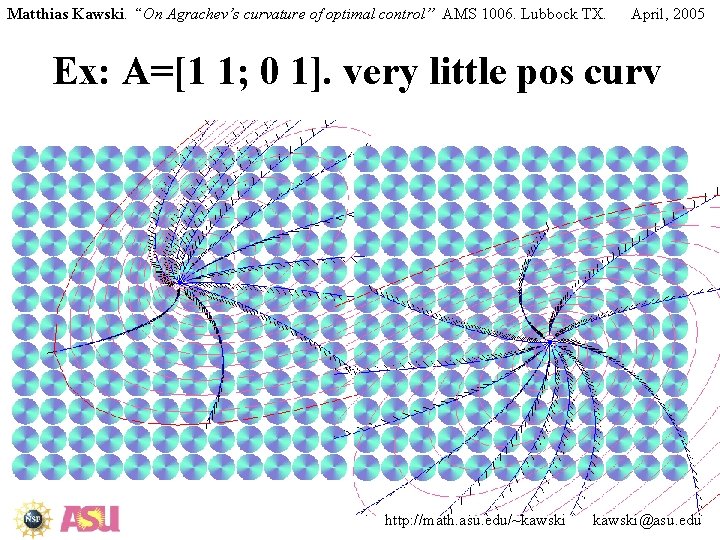
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Ex: A=[1 1; 0 1]. very little pos curv http: //math. asu. edu/~kawski@asu. edu

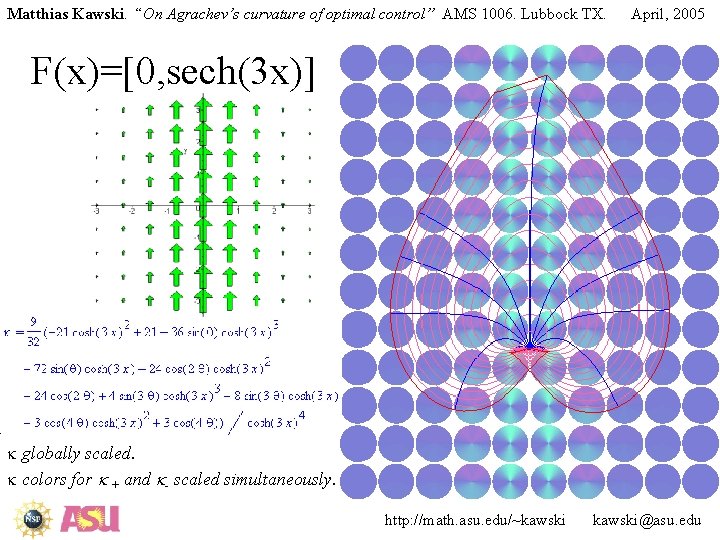
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 F(x)=[0, sech(3 x)] k globally scaled. k colors for k + and k- scaled simultaneously. http: //math. asu. edu/~kawski@asu. edu

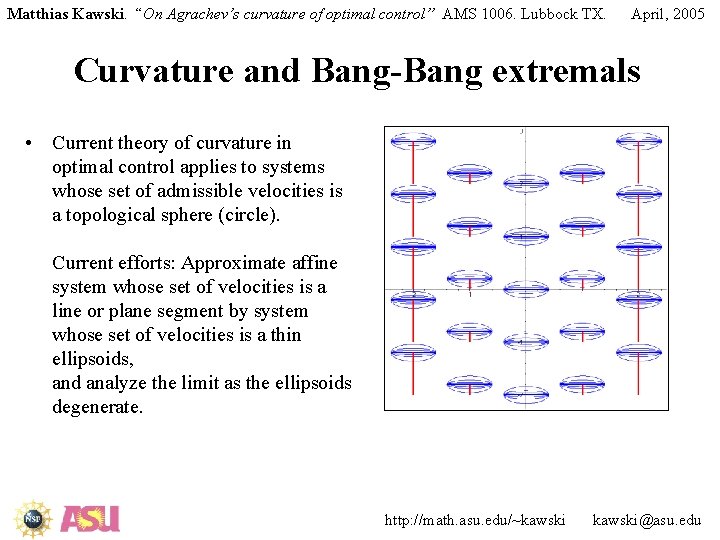
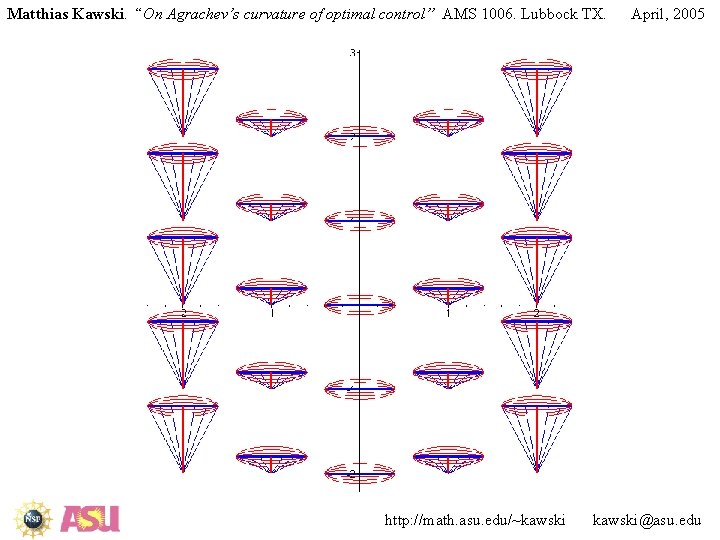
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Curvature and Bang-Bang extremals • Current theory of curvature in optimal control applies to systems whose set of admissible velocities is a topological sphere (circle). Current efforts: Approximate affine system whose set of velocities is a line or plane segment by system whose set of velocities is a thin ellipsoids, and analyze the limit as the ellipsoids degenerate. http: //math. asu. edu/~kawski@asu. edu

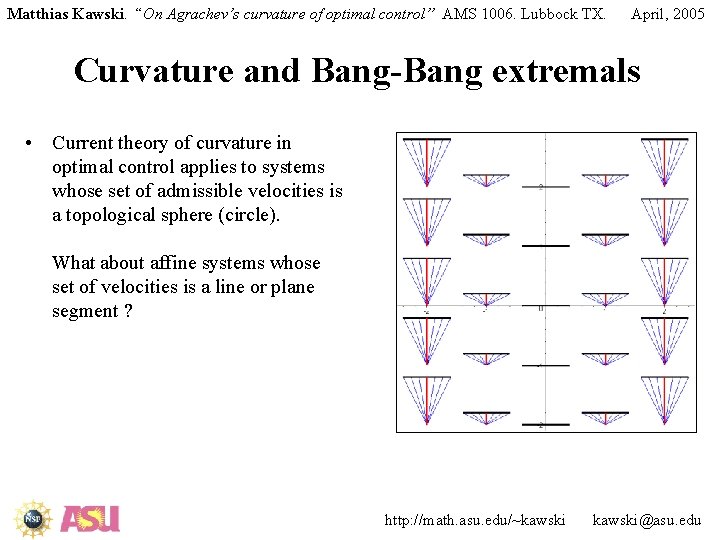
Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Curvature and Bang-Bang extremals • Current theory of curvature in optimal control applies to systems whose set of admissible velocities is a topological sphere (circle). What about affine systems whose set of velocities is a line or plane segment ? http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. April, 2005 Conclusion • • • Curvature of control: beautiful subject promising to yield new sufficiency results Even most simple classes of systems far from understood CAS and interactive visualization promise to be useful tools to scan entire classes of systems for interesting, “proof-worthy” properties. Some CAS open problems (“simplify”). Numerically fast implementation for JAVA – not yet. Zermelo’s problem particularly nice because everyone has intuitive understanding, wants to argue which way is best, then see and compare to the true optimal trajectories. Current efforts: Agrachev’s theory applies to systems whose set of admissible velocities is a topological sphere (circle). Current efforts: Approximate systems whose set of velocities is a line/plane… segment by thin ellipsoids and analyze the limit as the ellipsoids degenerate. http: //math. asu. edu/~kawski@asu. edu

Matthias Kawski. “On Agrachev’s curvature of optimal control” AMS 1006. Lubbock TX. http: //math. asu. edu/~kawski April, 2005 kawski@asu. edu