Matrizes Unidimensionais Definio n Matrizes unidimensionais ou arrays

Matrizes Unidimensionais

Definição n Matrizes unidimensionais ou arrays são áreas contíguas de memória que possuem o mesmo nome e o mesmo tipo n Para referir-se a uma localização ou elemento particular no array, são necessários o nome do array e o número da posição

Declaração de Arrays n n n Arrays possuem um número fixo de variáveis do mesmo tipo A declaração e a alocação de arrays são operações distintas (em alguns casos) Exemplos de declaração: Inteiro[] contadores Real[] resultados Texto[] nomes tipo[] identificador

Alocação Sintaxe: tipo[tamanho]; n Exemplos: n contadores = Inteiro[10] Resultados = Real[15] nomes = Texto[10]

Organização 0 1 2 3 4 5 6 7 8 9 contadores n n n Cada caixa é uma variável do tipo Inteiro Os números acima são os índices das variáveis Um array de tamanho 10 tem índices de 0 a 9 (em grande parte dos casos)

Índices de Arrays n n n Arrays podem conter qualquer tipo de valor Índices são usados para acessar valores específicos do array Exemplos: contadores[0] contadores[1] contadores[9] contadores[10] /* /* primeira variável em contadores*/ segunda variável em contadores*/ última variável em contadores */ erro */

Expressões como índices n n n Índices de array não precisam ser constantes Índices de Array necessitam ser expressões inteiras que resultam em um índice válido para o array Exemplos: contadores[i] contadores[2*i] contadores[I/2]

Inicialização n n n Arrays podem ser inicializados por uma lista de elementos dados Se a lista possui n elementos os índices serão de 0 a n – 1 Exemplo: Inteiro[] primos = {2, 3, 5, 7, 11, 13, 17, 19}

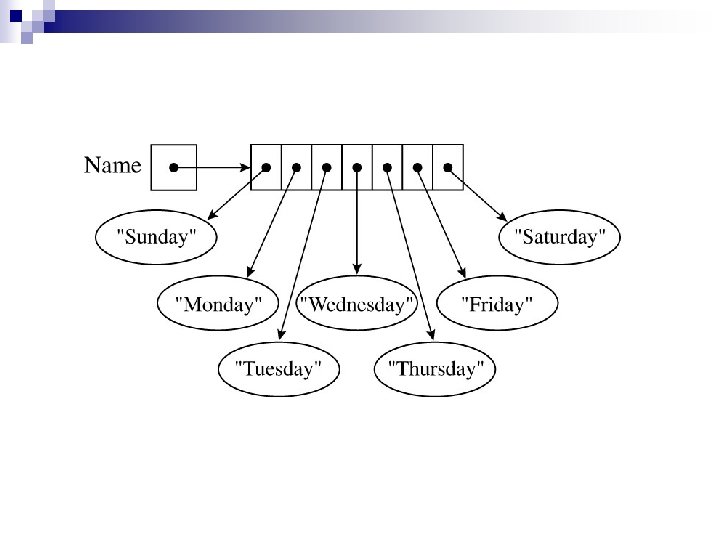
Inicializando Arrays de Texto[] NAME = { “Sunday”, “Monday”, “Tuesday”, “Wednesday”, “Thursday”, “Friday”, “Saturday”}

Repetição e Processamento n Inicializa contadores com 0, 10, 20, … , 90 Inteiro i=0 para(i < 10; i=i+1) faça contadores[i] = i * 10 fimpara n Imprime o conteúdo Inteiro i=0 para (i < 10; i=i+1) faça imprimir contadores[i] fimpara

Capacidade n n Arrays não podem crescer uma vez que eles foram alocados Você pode alocar mais espaço do que você acredita que vai precisar Se você escolher um valor baixo, ainda ficará sem espaço Não é necessário usar todos os elementos de um array (mas a memória total de um computador não é infinita)

Busca n Esta repetição termina logo que encontra o valor 90 armazenado em resulados Lógico found = falso Inteiro i = 0 Enquanto (i < size & !found) faça se (resultados[i] == x)então found = verdadeiro senão i=i+1 fimse fimenquanto

Busca n n Quando procurar por valores inteiros comparações exatas podem ser feitas (A[i] == key) Comparar dois valores Reais para igualdade nem sempre será uma operação correta Um modo melhor para Reais é ((A[i]–key) < epsilon) Epsilon deve ser um valor pequeno aceitável para a aplicação

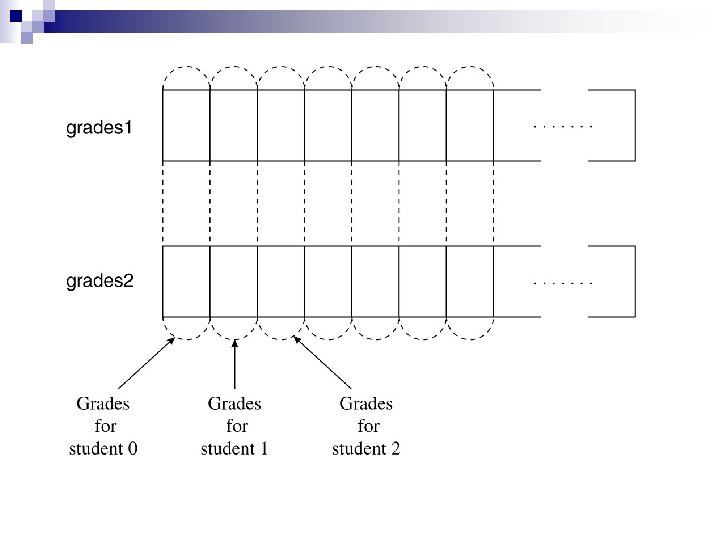
Processando Arrays simultaneamente n Esta repetição conta quantos de estudantes melhoraram o rendimento no segundo exame inteiro melhorou = 0 Inteiro i=0 para (i < size; i=i+1) faça se (grades 1[i] < grades 2[i]) então melhorou = melhorou+1 fimse fimpara

Ordenação por seleção n n n Encontrar o menor elemento entre A[0]. . A[n-1] e chamálo A[min] trocar A[0] e A[min] fazendo com que A[0] contenha o menor elemento e A[1]. . A[n-1] sejam não ordenados Agora, encontrar o menor elemento entre A[1]. . A[n-1] e chamá-lo A[min] trocar A[1] e A[min] de modo que A[1] contenha o segundo menor elemento A[2]. . A[n-1] sejam não ordenados Faça de maneira similar para o restante dos elementos

Selection. Sort – parte 1 Algoritmo selection. Sort () Início /*inserir a criação/leitura do array A*/ Inteiro i=0 para ( i < size; i=i+1) faça inteiro j=i+1 inteiro min = i para(j < size; j=j+1)faça se (A[j] < A[min]) então min =j fimse fimpara

Selection. Sort – parte 2 Real temp = A[i] = A[min] = temp fimpara fim

Bubble Sort Procedimento bubble. Sort (Inteiro[] &vet) Início Inteiro i=0 para ( i < size; i=i+1) faça inteiro j=i+1 para(j < size; j=j+1)faça se (vet[j] < vet[i]) então inteiro aux =vet[i]=vet[j]=aux fimse fimpara fim

Arrays multidimensionais Arrays podem ter mais do que uma dimensão n As chamadas matrizes podem ser vistas como arrays de arrays n Sintaxe Inteiro[][] matriz = Inteiro[10] n

Exercício 1 n Completar o algoritmo selectio. Sort com a parte que está faltando

Exercício 2 n Faça um algoritmo que leia 20 números entre 100, inclusive. O algoritmo deve imprimir o número somente se ele não for uma duplicata de um número lido anteriormente

Exercício 3 n Utilize uma matriz bidimensional para resolver o seguinte problema: Uma empresa tem 4 vendedores que vendem 5 produtos. Uma vez por dia, cada vendedor entrega uma nota de cada tipo de produto diferente vendido. Cada nota contém 1) número do vendedor, 2) número do produto e 3) valor total vendido deste produto em reais.

Exercício 3 Faça um programa que leia o total de notas para cada produto para cada vendedor e calcule a comissão de cada vendedor. A comissão é calculada pela seguinte equação: n Comissão = 10%*(total. Prod 1)+ 20%*(total. Prod 2)+ 10%*(total. Prod 3)+ 20%*(total. Prod 4)+ 10%*(total. Prod 5) n