Matrizen und Matrizenoperationen in der Anwendung Prof Dr











- Slides: 14

Matrizen und Matrizenoperationen in der Anwendung Prof. Dr. Wolfgang Konen TH Köln Wolfgang Konen, TH Köln – Mathematik Seite - 1

Matrizen / Überblick © Ziele dieses Kapitels Ø Wieso Matrizen Ø Definition Matrix, Matrixmultiplikation Ø Anwendung Produktionsplanung Ø Basiswechsel Wolfgang Konen, TH Köln – Mathematik Seite - 2

Motivation Matrizen © Beispiel Produktionsplanung Ø Aus k=1, . . . , 3 Rohstoffen Rk werden Endprodukte En hergestellt. Die benötigten Rohstoffeinheiten je Einheit En sind: Ø Wenn die Rohstoffpreise pk je Einheit Rk sind, was sind dann die Kosten qn je Einheit En ? Ø LGS: Lineares Gleichungssystem Wolfgang Konen, TH Köln – Mathematik Seite - 3

Motivation Matrizen © Mathematiker sind (schreib-) faule Leute Ø Statt Ø schreiben sie einfacher Wolfgang Konen, TH Köln – Mathematik Seite - 4

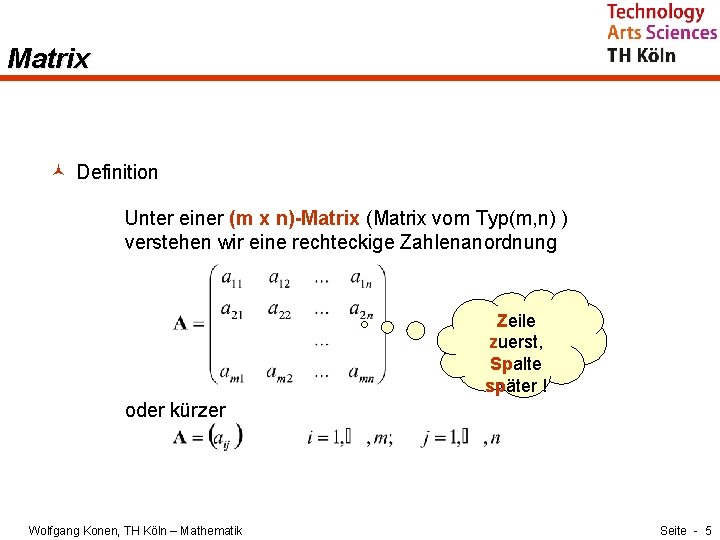
Matrix © Definition Unter einer (m x n)-Matrix (Matrix vom Typ(m, n) ) verstehen wir eine rechteckige Zahlenanordnung Zeile zuerst, Spalte später ! oder kürzer Wolfgang Konen, TH Köln – Mathematik Seite - 5

Sonderfälle © Spalten- und Zeilenmatrix Eine (m x 1)-Matrix heißt Spaltenmatrix (Vektor) nur ein Index ! Eine (1 x n)-Matrix heißt Zeilenmatrix (Zeilenvektor) Wolfgang Konen, TH Köln – Mathematik Seite - 6

Multiplikation von Matrizen © Definition Es sei A eine (n x k)-Matrix und B eine (k x p)-Matrix. Unter dem Produkt C=A·B verstehen wir die (n x p)Matrix mit heißt auch inneres Produkt, weil über die inneren Indizes summiert wird Wolfgang Konen, TH Köln – Mathematik Seite - 7

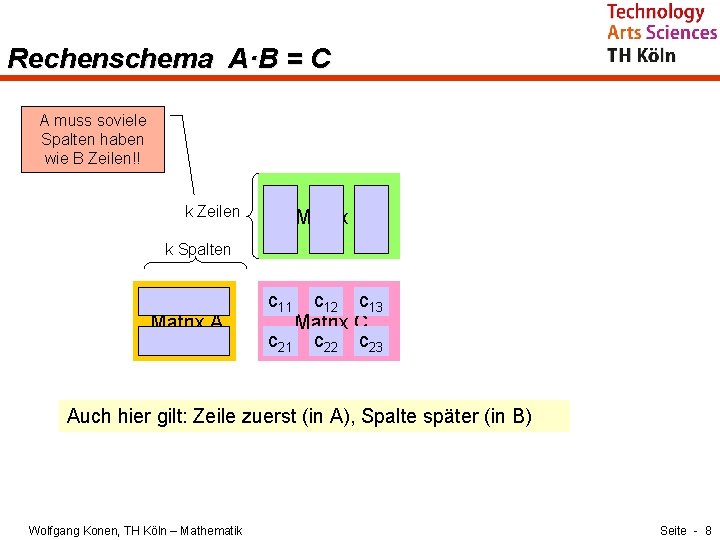
Rechenschema A·B = C A muss soviele Spalten haben wie B Zeilen!! k Zeilen Matrix B k Spalten Matrix A c 11 c 12 c 13 Matrix C c 21 c 22 c 23 Auch hier gilt: Zeile zuerst (in A), Spalte später (in B) Wolfgang Konen, TH Köln – Mathematik Seite - 8

Anwendung Produktionsplanung © Die Definition Matrixmultiplikation ist genau so gewählt, dass sich wieder das LGS ergibt: Ø bedeutet ausmultipliziert Wolfgang Konen, TH Köln – Mathematik Seite - 9

Die Vorteile Q 2 1. Quartalspreise: Q 1 Q 3 Q 4 Ø Gelten in jedem Quartal andere Rohstoffpreise, so haben wir eine kompakte Darstellung und Berechnungsform der Endpreise. Wolfgang Konen, TH Köln – Mathematik Seite - 10

Die Vorteile 2. Wertstoffketten, Zwischenprodukte, „Basiswechsel“: Ø Rohstoffe Rk Zwischenprodukte Zm Endprodukte En Ø Gegeben die Rohstoffpreise p, wieviel kostet eine Einheit jedes Endproduktes? Wolfgang Konen, TH Köln – Mathematik Seite - 11

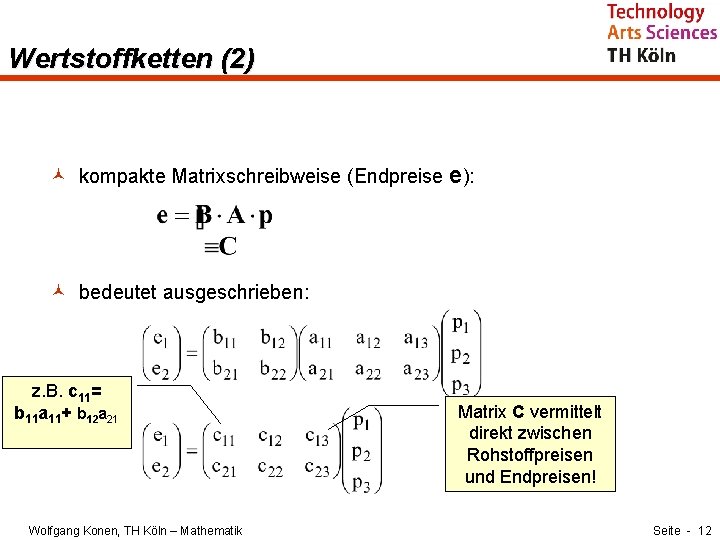
Wertstoffketten (2) © kompakte Matrixschreibweise (Endpreise e): © bedeutet ausgeschrieben: z. B. c 11= b 11 a 11+ b 12 a 21 Wolfgang Konen, TH Köln – Mathematik Matrix C vermittelt direkt zwischen Rohstoffpreisen und Endpreisen! Seite - 12

Wertstoffketten (3) Dieses Beispiel zeigt, daß folgendes gilt: © Die Multiplikation eines Vektors mit einer Matrix bildet einen Vektor (hier: p) auf einen neuen Vektor (hier: e)ab. © Die Hintereinanderausführung zweier solcher Abbildungen (hier erst die Multiplikation mit der Matrix A, anschließend die Multiplikation mit B) entspricht gerade der Multiplikation mit der Matrix C = BA. Das Matrizenprodukt wird gerade so definiert, daß es diese Eigenschaft hat. Wolfgang Konen, TH Köln – Mathematik Seite - 13

Zusammenfassung © Matrizen: kompakte Darstellung von LGS © Vektor als Spezialfall einer Matrix © Matrixmultiplikation © Matrizen vermitteln Wechsel zwischen Koordinatensystemen (Wertstoffketten, „Basiswechsel“) Wolfgang Konen, TH Köln – Mathematik Seite - 14
 Matrizen praktische anwendung
Matrizen praktische anwendung Nmatrix
Nmatrix Rechnen
Rechnen Magnesiumbad anwendung
Magnesiumbad anwendung Sortieralgorithmen anwendung
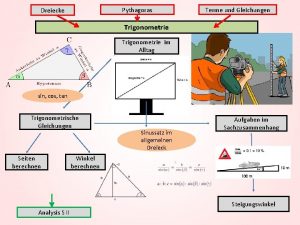
Sortieralgorithmen anwendung Trigonometrie im alltag
Trigonometrie im alltag Salviathymol unverdünnt anwenden
Salviathymol unverdünnt anwenden Entwicklungsmodi st.galler management modell
Entwicklungsmodi st.galler management modell Piezoelement funktionsweise
Piezoelement funktionsweise Siberian pure herbs massage balsam
Siberian pure herbs massage balsam Kommunikationsplan aufbau
Kommunikationsplan aufbau Praktische anwendung differentialrechnung
Praktische anwendung differentialrechnung Uhrengetriebe
Uhrengetriebe Leiter test
Leiter test Der aufbau der burg
Der aufbau der burg