Matriz uma tabela de elementos dispostos segundo linhas

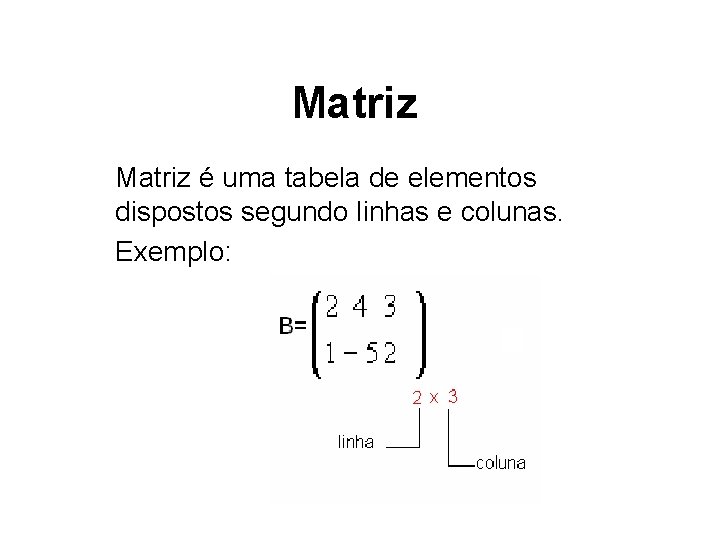
Matriz é uma tabela de elementos dispostos segundo linhas e colunas. Exemplo:

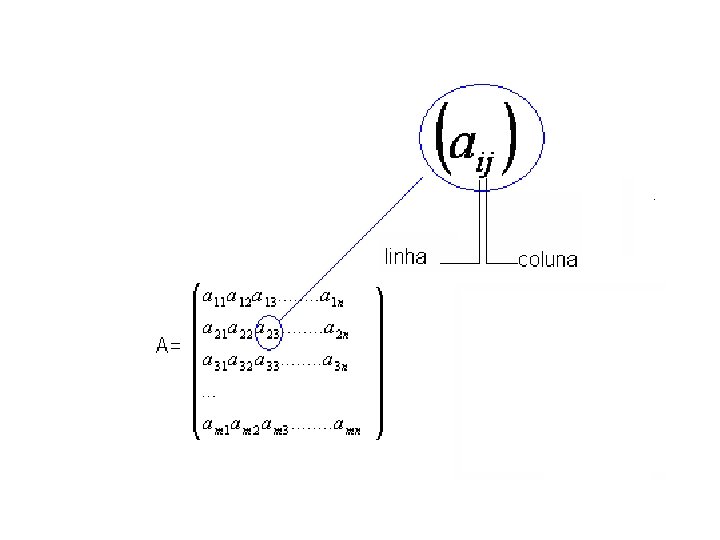
Representação de uma Matriz m x n - ordem da matriz

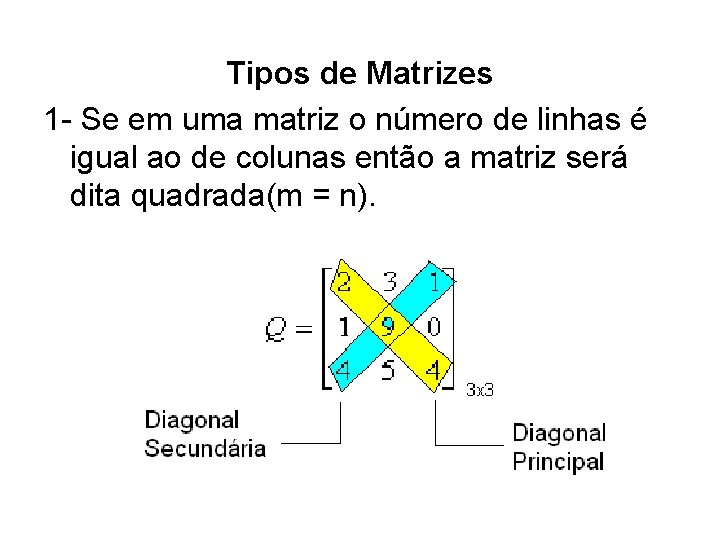
Tipos de Matrizes 1 - Se em uma matriz o número de linhas é igual ao de colunas então a matriz será dita quadrada(m = n).

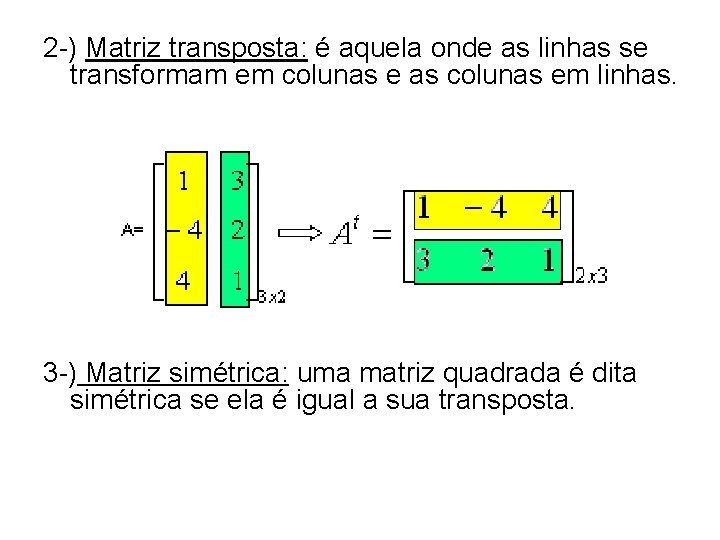
2 -) Matriz transposta: é aquela onde as linhas se transformam em colunas e as colunas em linhas. 3 -) Matriz simétrica: uma matriz quadrada é dita simétrica se ela é igual a sua transposta.

Obs: 1)Se , dizemos que a matriz A é simétrica. 2) Se , dizemos que a matriz A é antisimétrica. É óbvio que as matrizes simétricas e anti-simétricas são quadradas. 3) sendo A uma matriz anti-simétrica , temos que (matriz nula).

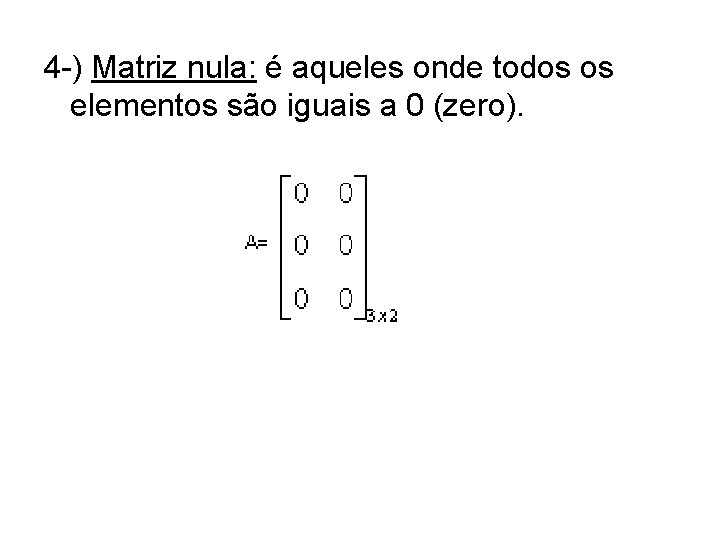
4 -) Matriz nula: é aqueles onde todos os elementos são iguais a 0 (zero).

5 -) Matriz identidade ou unidade: é uma matriz quadrada onde os elementos da diagonal principal são todos iguais a 1 e os demais 0 (zero).

6 -) Matriz triangular: é matriz quadrada onde todos os elementos acima ou a baixo da diagonal principal ou secundária são todos iguais a 0 (zero).

7 -) Matriz linha: é aquela que possui apenas uma linha. 8 -) Matriz coluna: é aquela que possui apenas uma coluna.

Operações com Matrizes Adição e Subtração: Acontece com matrizes de mesma ordem, e são obtidos somando-se ou subtraindo-se dos elementos correspondentes às duas matrizes. Ex.

Multiplicação de um Nº. Real por uma Matriz O número real multiplica cada elemento da matriz. Ex.

Produto de Matrizes: Para que exista o produto de duas matrizes A e B , o número de colunas de A , tem de ser igual ao número de linhas de B.

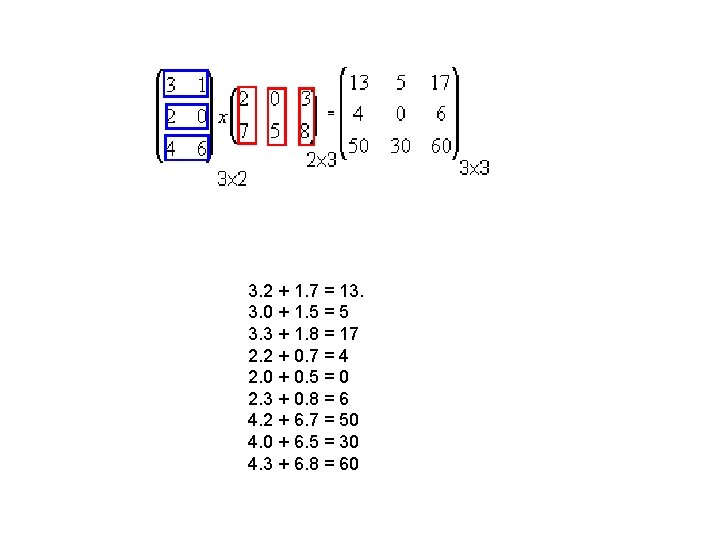
3. 2 + 1. 7 = 13. 3. 0 + 1. 5 = 5 3. 3 + 1. 8 = 17 2. 2 + 0. 7 = 4 2. 0 + 0. 5 = 0 2. 3 + 0. 8 = 6 4. 2 + 6. 7 = 50 4. 0 + 6. 5 = 30 4. 3 + 6. 8 = 60

Nota: O produto de matrizes é uma operação não comutativa, ou seja: A x B nem sempre é igual a B x A. Quando A x B = B x A, dizemos que as matrizes A e B comutam.

Inversa de uma matriz: Dada a matriz quadrada A de ordem n, chamamos a inversa de A, se existir, a matriz tal que : Se A admitir inversa dizemos que ela é inversível (invertível). Caso não exista a matriz inversa, dizemos que a matriz A é SINGULAR ou NÃO INVERSÍVEL.

Exemplo: Determine, se existir a inversa da matriz

• http: //www. ficharionline. com/Exibe. Conteudo. php 5? idconteu do=5819 • http: //www. brasilescola. com/matematica/matriz. htm • http: //www. paulomarques. com. br/arq 12 -1. htm