Matrix Multiplication Winograd Multiplication n Vv 1 v

Matrix Multiplication

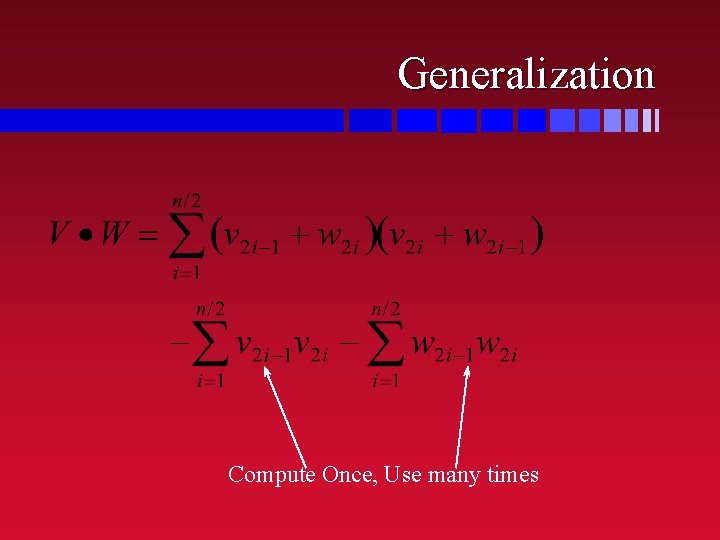
Winograd Multiplication n V=(v 1, v 2, v 3, v 4) n W=(w 1, w 2, w 3, w 4) n V·W=v 1 w 1+v 2 w 2+v 3 w 3+v 4 w 4 n V·W=(v 1+w 2)(v 2+w 1) + (v 3+w 4)(v 4+w 3) -v 1 v 2 -v 3 v 4 -w 1 w 2 -w 3 w 4

Generalization Compute Once, Use many times

Analysis Ordinary Matrix Multiply, n 3 n Winograd’s Matrix Multiply, (n 3/2)+n 2 n Additions, n 3 -n 2, v. s. (3/2)n 3+2 n 2 -2 n n Lower Bound, Best known is n 2 n Best known Upper Bound and Best Known Lower Bound are not the same n

Two By Two Multiplication n c 1, 1=a 1, 1 b 1, 1+a 1, 2 b 2, 1 n c 1, 2=a 1, 1 b 1, 2+a 1, 2 b 2, 2 n c 2, 1=a 2, 1 b 1, 1+a 2, 2 b 2, 1 n c 2, 2=a 2, 1 b 1, 2+a 2, 2 b 2, 2

2 x 2 Works for Matrices C 1, 1=A 1, 1 B 1, 1+A 1, 2 B 2, 1 n C 1, 2=A 1, 1 B 1, 2+A 1, 2 B 2, 2 n C 2, 1=A 2, 1 B 1, 1+A 2, 2 B 2, 1 n C 2, 2=A 2, 1 B 1, 2+A 2, 2 B 2, 2 n A 1, 1 A 1, 2 A 2, 1 A 2, 2 ´ B 1, 1 B 1, 2 B 2, 1 B 2, 2 = C 1, 1 C 1, 2 C 2, 1 C 2, 2

Divide and Conquer? Assume matrices of size 2 n´ 2 n n Multiplications: M(n) = 8 M(n/2), M(1)=8 n Additions: A(n) = 8 A(n/2)+n 2 n M(n) = 8 lg n = nlg 8 = n 3 n Additions are also Q(n 3), but point is moot n Can we reduce the 8 multiplications in the base equations n

Strassen’s Equations n x 1=(a 1, 1+a 2, 2)(b 1, 1+b 2, 2) n x 2=(a 2, 1+a 2, 2) b 1, 1 n x 3=a 1, 1(b 1, 2 -b 2, 2) n x 4=a 2, 2(b 2, 1 -b 1, 1) n x 5=(a 1, 1+a 1, 2) b 2, 2 n x 6=(a 2, 1 -a 1, 1)(b 1, 1+b 1, 2) n x 7=(a 1, 2 -a 2, 2)(b 2, 1+b 2, 2)

Using The Equations n c 1, 1 = x 1 + x 4 - x 5 + x 7 n c 1, 2 = x 3 + x 5 n c 2, 1 = x 2 + x 4 n c 2, 2 = x 1 + x 3 - x 2 + x 6

Analysis of Strassen Only 7 multiplications are used n Will work with matrices, because associative property is not used n Multiplications: M(n) = 7 M(n/2), M(1) = 7 n Additions: A(n) = 7 A(n/2)+18(n 2/4) n M(n) = 7 lg n = nlg 7 = n 2. 81 n Additions are also Q(n 2. 81) n First algorithm to break the n 3 “barrier” n