Matrix Multiplication Hungyi Lee Matrix Multiplication Given two

Matrix Multiplication Hung-yi Lee

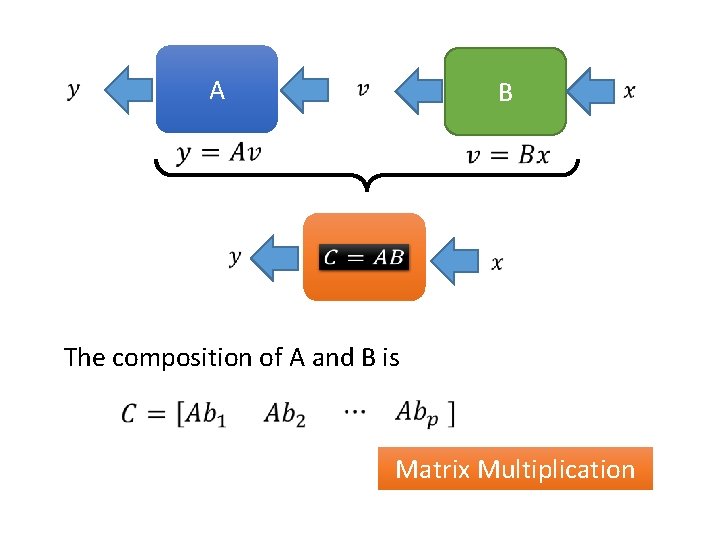
Matrix Multiplication • Given two matrices A and B, the (i, j)-entry of AB is the inner product of row i of A and column j of B A B

Matrix Multiplication • Given two matrices A and B, the (i, j)-entry of AB is the inner product of row i of A and column j of B =

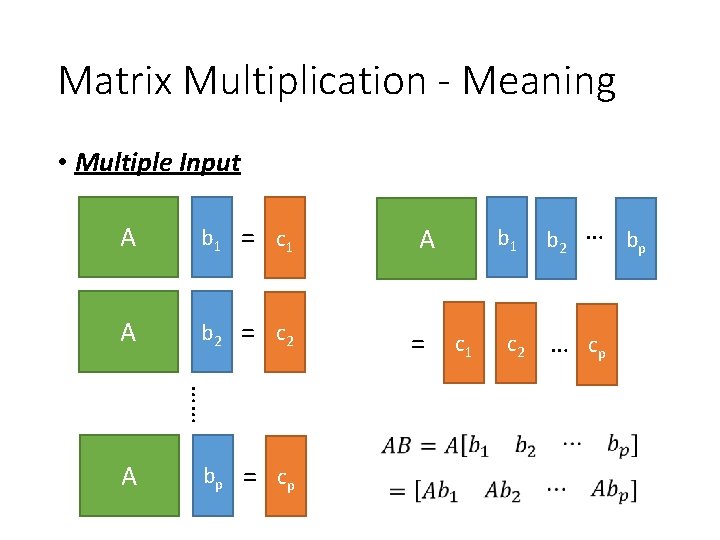
Matrix Multiplication - Meaning • Multiple Input A b 1 = c 1 A b 2 = c 2 …… A bp = c p A = b 1 c 2 b 2 … bp … cp

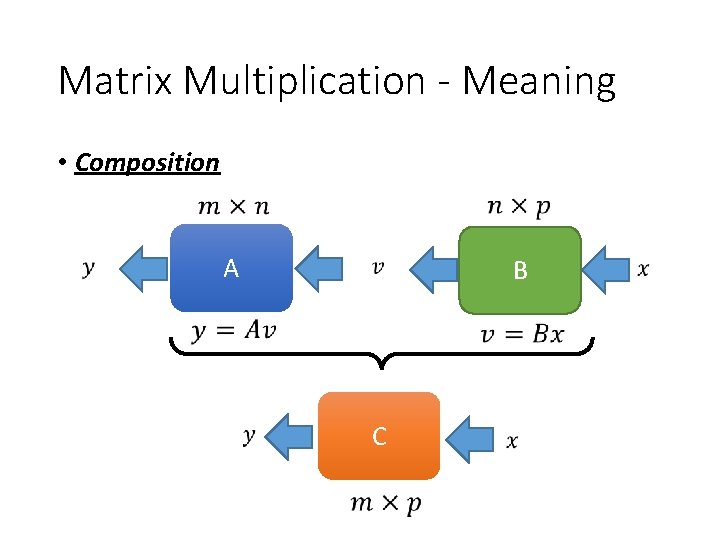
Matrix Multiplication - Meaning • g f g◦f Matrix multiplication is the composition of two linear functions.

Matrix Multiplication - Meaning • Composition A B C

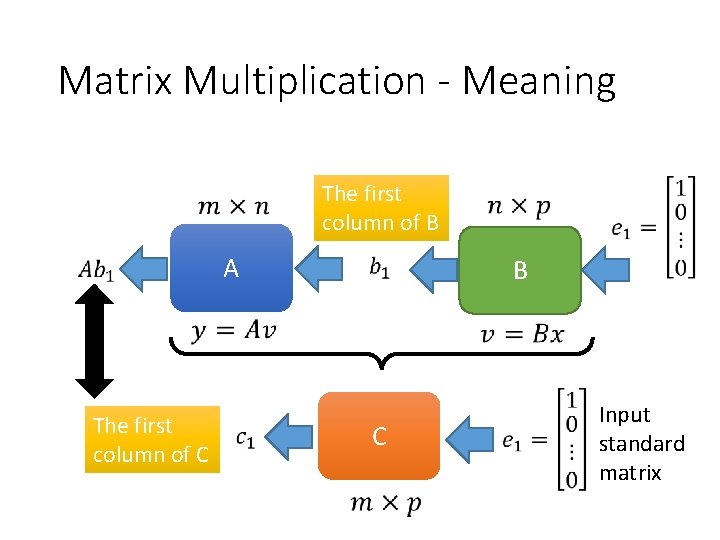
Matrix Multiplication - Meaning The first column of B A The first column of C B C Input standard matrix

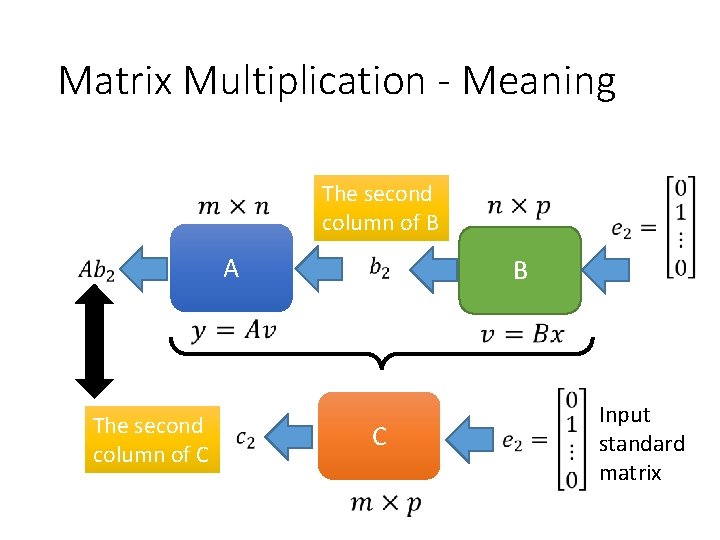
Matrix Multiplication - Meaning The second column of B A The second column of C B C Input standard matrix

A B C The composition of A and B is Matrix Multiplication

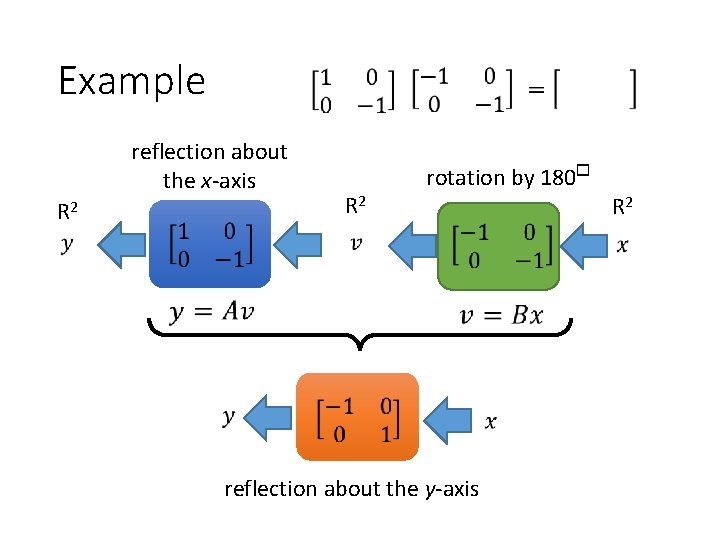
Example reflection about the x-axis R 2 rotation by 180 reflection about the y-axis R 2

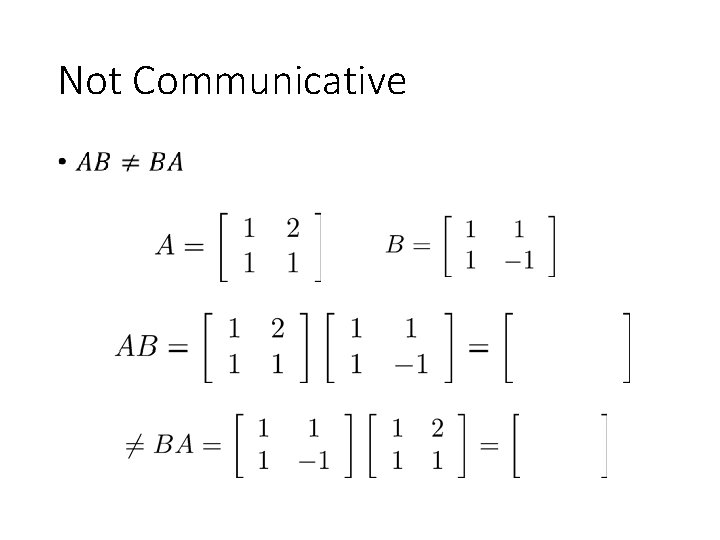
Not Communicative •

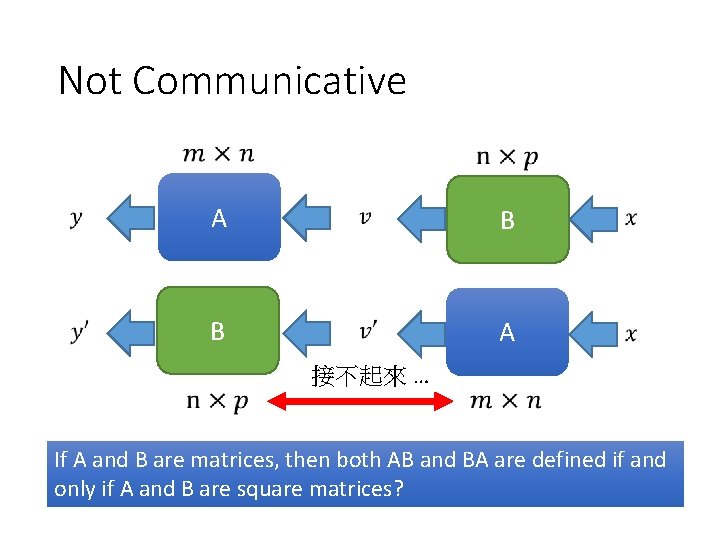
Not Communicative A B B A 接不起來 … If A and B are matrices, then both AB and BA are defined if and only if A and B are square matrices?

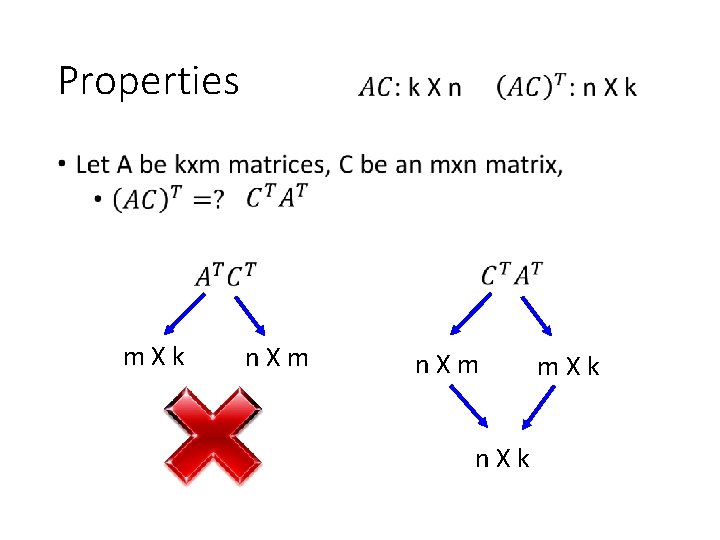
Properties • Let A and B be k x m matrices, C be an m x n matrix, and P and Q be n x p matrices • For any scalar s, s(AC) = (s. A)C = A(s. C) • (A + B)C = AC + BC • C(P+Q)=CP+CQ • Ik. A = AIm • The product of any matrix and a zero matrix is a zero matrix • Power of square matrices: A Mn n, Ak = A A A (k times), and by convention, A 1 = A, A 0 = In.

Properties • m. Xk n. Xm n. Xk m. Xk

Special Matrix • Diagonal Matrix • Symmetric Matrix AAT and ATA are square and symmetric

Augmentation and Partition • Augment: the augment of A and B is [A B] • Partition:

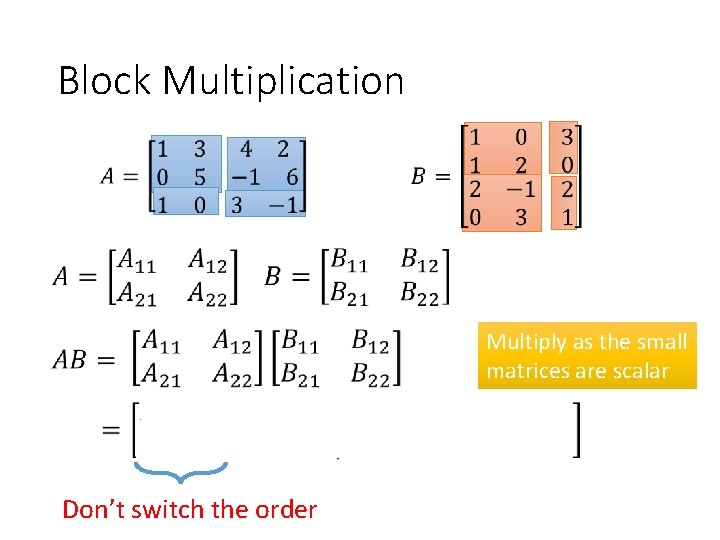
Block Multiplication Multiply as the small matrices are scalar Don’t switch the order

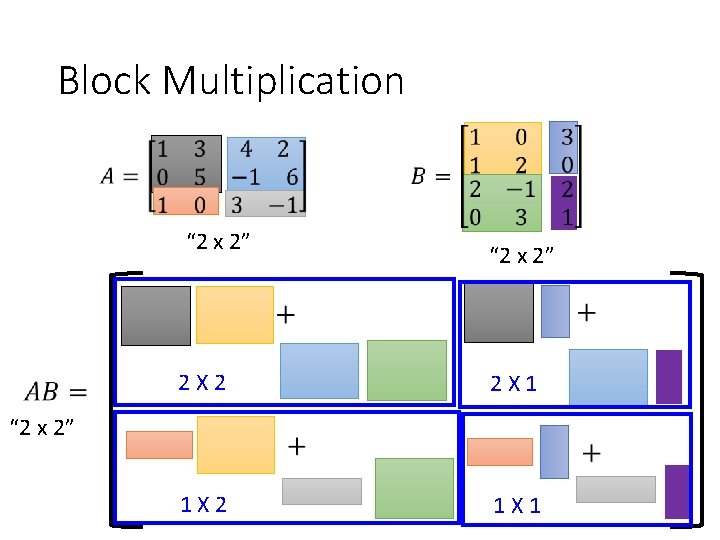
Block Multiplication “ 2 x 2” 2 X 2 2 X 1 1 X 2 1 X 1 “ 2 x 2”

Block Multiplication

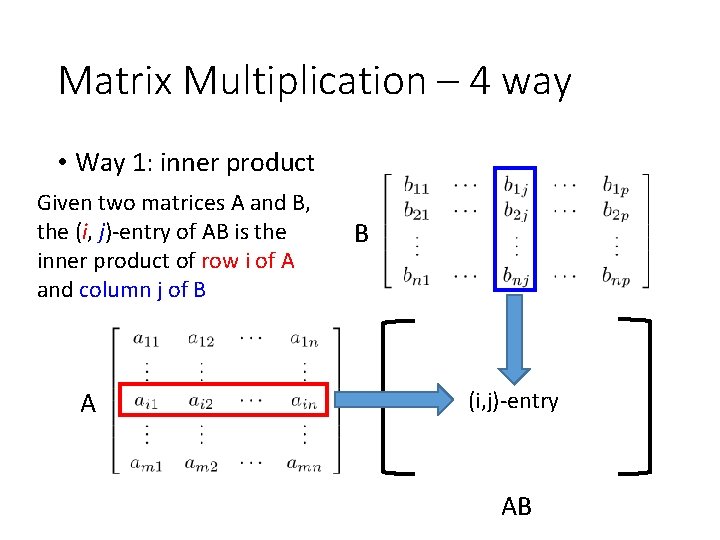
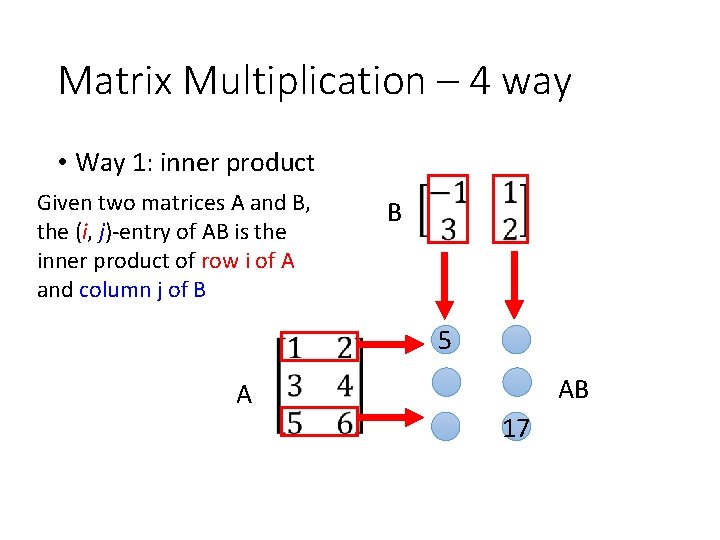
Matrix Multiplication – 4 way • Way 1: inner product Given two matrices A and B, the (i, j)-entry of AB is the inner product of row i of A and column j of B A B (i, j)-entry AB

Matrix Multiplication – 4 way • Way 1: inner product Given two matrices A and B, the (i, j)-entry of AB is the inner product of row i of A and column j of B B 5 AB A 17

Matrix Multiplication – 4 way • Way 2: Linear combination of columns …… = … The first column …… … The second column ……

Matrix Multiplication – 4 way • Way 2: Linear combination of columns = The first column The second column

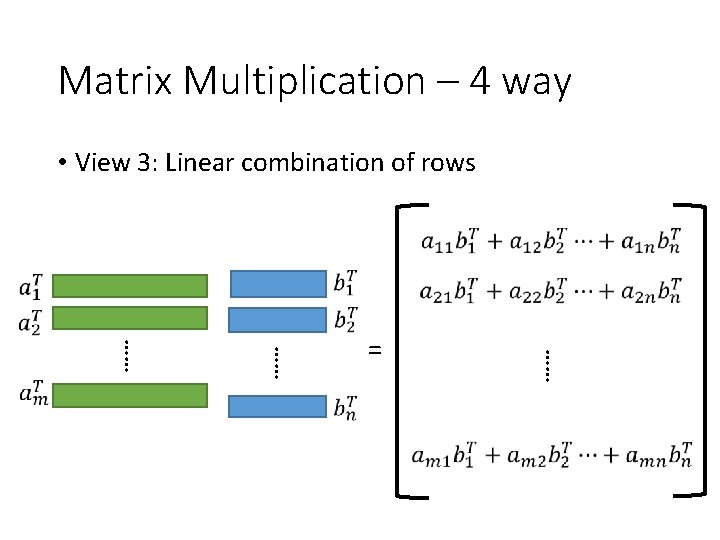
Matrix Multiplication – 4 way • View 3: Linear combination of rows …… …… …… =

Matrix Multiplication – 4 way • Way 3: Linear combination of rows The first row = The second row The third row

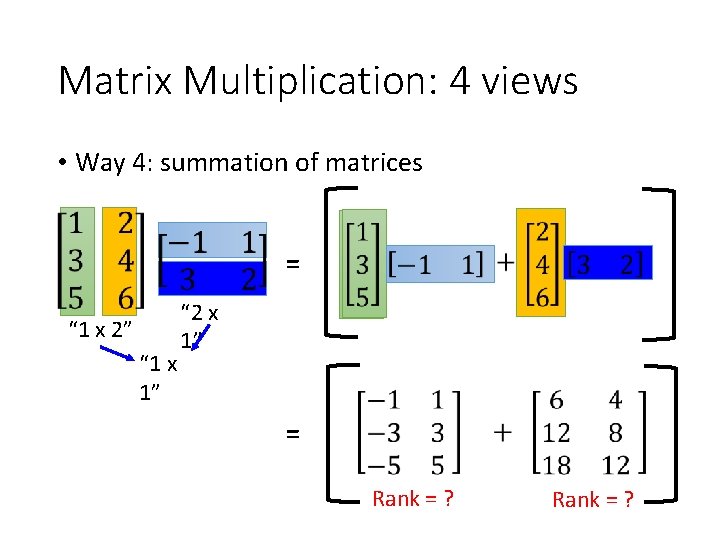
Matrix Multiplication: 4 views • View 4: Summation of matrices …… …… matrices

Matrix Multiplication: 4 views • Way 4: summation of matrices = “ 1 x 2” “ 1 x 1” “ 2 x 1” = Rank = ?

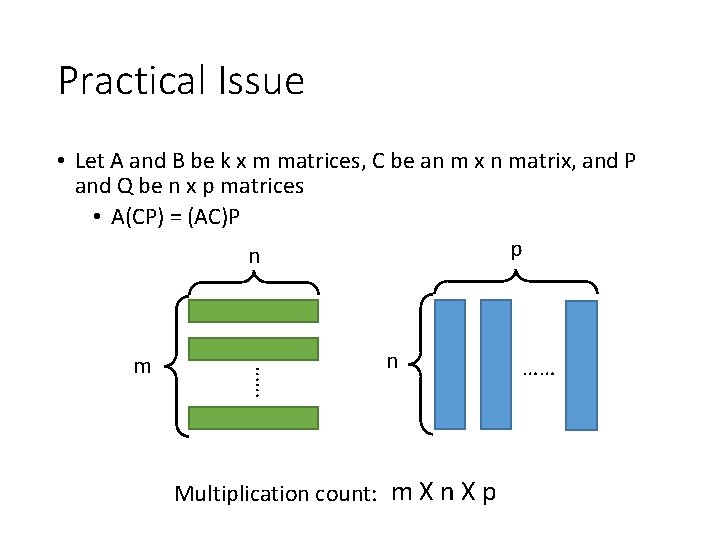
Practical Issue • Let A and B be k x m matrices, C be an m x n matrix, and P and Q be n x p matrices • A(CP) = (AC)P p n …… m n Multiplication count: m X n X p ……

Practical Issue k=1 m=1000 n=1 p=1000 • Let A and B be kxm matrices, C be an mxn matrix, and P and Q be nxp matrices • A(CP) = (AC)P A C k. Xm m. Xn A CP k. Xm m. Xp P n. Xp m. Xn. Xp 106 k. Xm. Xp 106 A C P k. Xm m. Xn AC P k. Xn n. Xp k. Xm. Xn 103 k. Xn. Xp 103

Practical Issue - GPU 10000 Multiplying two 10000 X 10000 matrices CPU GPU (GTX 980 Ti) More than 20 times faster