Matrix Models and Matrix Integrals A Mironov Lebedev

Matrix Models and Matrix Integrals A. Mironov Lebedev Physical Institute and ITEP

New structures associated with matrix integrals mostly inspired by studies in low-energy SUSY Gauge theories (F. Cachazo, K. Intrilligator, C. Vafa; R. Dijkgraaf, C. Vafa) low-energy effective action in N=2 SUSY gauge theory Prepotential massless BPS-states Superpotential in minima in N=1 SUSY gauge theory

• Standard dealing with matrix models • Dijkgraaf – Vafa (DV) construction (G. Bonnet, F. David, B. Eynard, 2000) • Virasoro constraints (=loop equations, =Schwinger-Dyson equations, =Ward identities) • Matrix models as solutions to the Virasoro constraints (Dmodule) • What distinguishes the DV construction. On Whitham hierarchies and all that

Hermitean 1 -matrix integral: W(l) is a polynomial 1/N – expansion (saddle point equation):

Constraints:

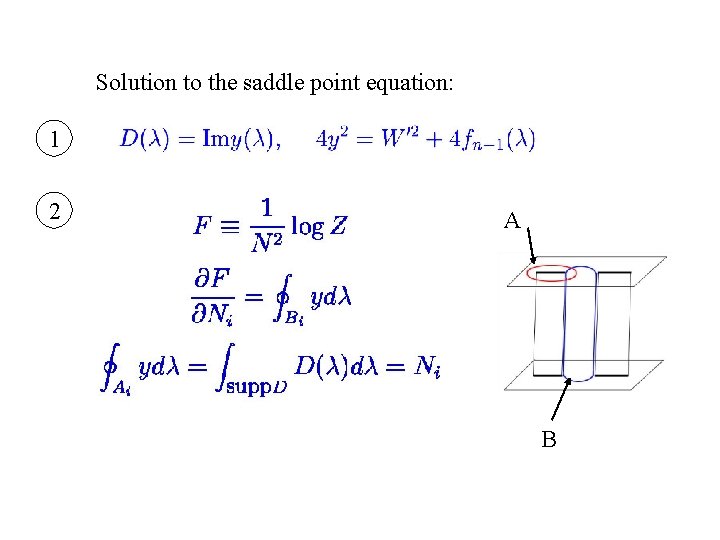
Solution to the saddle point equation: 1 2 A B

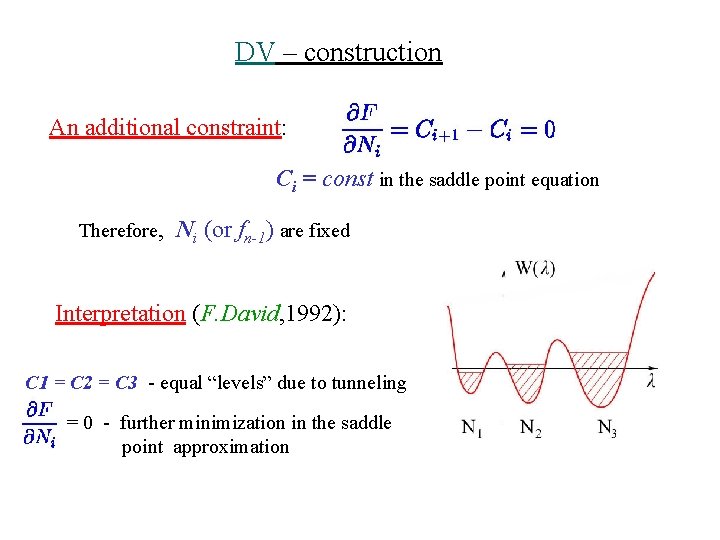
DV – construction An additional constraint: Ci = const in the saddle point equation Therefore, Ni (or fn-1) are fixed Interpretation (F. David, 1992): C 1 = C 2 = C 3 - equal “levels” due to tunneling = 0 - further minimization in the saddle point approximation

Let Ni be the parameters! It can be done either by introducing chemical potential or by removing tunneling (G. Bonnet, F. David, B. Eynard) i. e.

Virasoro & loop equations A systematic way to construct these expansions (including higher order corrections) is Virasoro (loop) equations Change of variables in leads to the Ward identities: - Virasoro (Borel sub-) algebra

We define the matrix model as any solution to the Virasoro constraints (i. e. as a D-module). DV construction is a particular case of this general approach, when there exists multi-matrix representation for the solution. PROBLEMS: 1) How many solutions do the Virasoro constraints have? 2) What is role of the DV - solutions? 3) When do there exist integral (matrix) representations?

The problem number zero: How is the matrix model integral defined at all? It is a formal series in positive degrees of tk and we are going to solve Virasoro constraints iteratively. tk have dimensions (grade): [tk]=k (from Ln or matrix integral) ck. . . dimensionful all ck. . . = 0

The Bonnet - David - Eynard matrix representation for the DV construction is obtained by shifting or Then W (or Tk) can appear in the denominators of the formal series in tk We then solve the Virasoro constraints with the additional requirement

Example 1 and The only solution to the Virasoro constraints is the Gaussian model: - the integral is treated as the perturbation expansion in tk Example 2 and One of many solutions is the Bonnet - David - Eynard n-parametric construction Ni can be taken non-integer in the perturbative expansion

Where . Note that We again shift the couplings and consider Z as a power series in tk’s but not in Tk’s: i. e. one calculates the moments

Example: Cubic potential at zero couplings gives the Airy equation Solution: Two solutions = two basic contours. Contour: the integrand vanishes at its ends to guarantee Virasoro constraints! The contour should go to infinity where

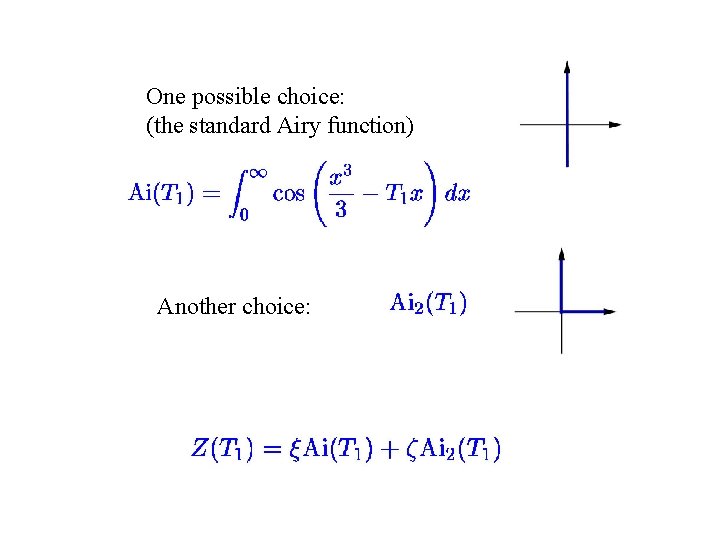
One possible choice: (the standard Airy function) Another choice:

Asymptotic expansion of the integral Saddle point equation has two solutions: Generally W‘(x) = 0 has n solutions n-1 solutions have smooth limit Tn+1 0

Cubic example:

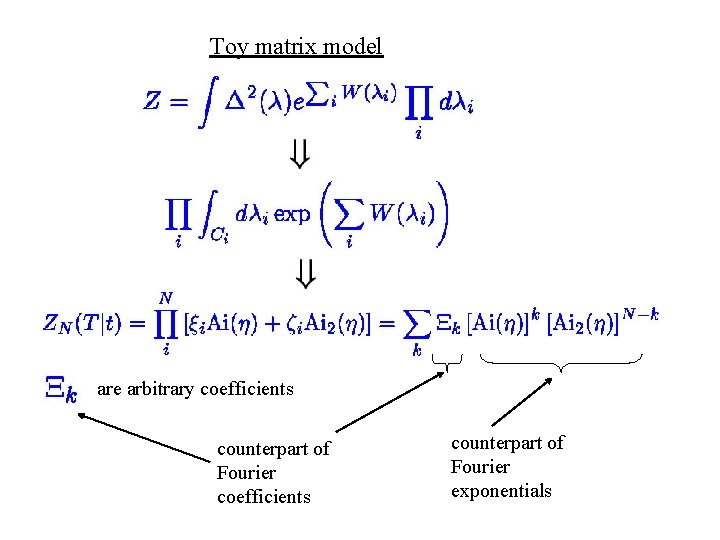
Toy matrix model are arbitrary coefficients counterpart of Fourier exponentials

General solution (A. Alexandrov, A. Morozov) At any order in 1/N the solution Z of the Virasoro equations is uniquely defined by an arbitrary function of n-1 variables (n+2 variables fixed combinations) E. g. In the curve Tk enter through n-1

Claim where Uw is an (infinite degree) differential operator in that does not depend of the choice of arbitrary function Tk (T) Therefore: some proper basis DV construction provides us with a possible basis:

DV basis: 1) Ni = const, i. e. This fixes fn uniquely. 2) (More important) adding more times Tk does not change analytic structures (e. g. the singularities of should be at the same branching points which, however, begin to depend on Tk ) Constant monodromies Whitham system In planar limit: This concrete Virasoro solution describes Whitham hierarchy (L. Chekhov, A. M. ) and log Z is its t -function. It satisfies Witten-Dijkgraaf-Verlinde equations (L. Chekhov, A. Marshakov, A. M. , D. Vasiliev)

Invariant description of the DV basis: - monodromies of minima of W(x) can be diagonalized DV – basis: eigenvectors of (similarly to the condition )

Seiberg – Witten – Whitham system Operator relation (not proved) : Conditions: blowing up to cuts on the complex plane Therefore, in the basis of eigenvectors, can be realized as Seiberg - Witten - Whitham system

Conclusion • The Hermitean one-matrix integral is well-defined by fixing an arbitrary polynomial Wn+1(x). • The corresponding Virasoro constraints have many solutions parameterized by an arbitrary function of n-1 variables. • The DV - Bonnet - David - Eynard solution gives rise to a basis in the space of all solutions to the Virasoro constraints. • This basis is distinguished by its property of preserving monodromies, which implies the Whitham hierarchy. The t -function of this hierarchy is associated with logarithm of the matrix model partition function.