Matrix Factorizations Singular Value Decomposition Presented by Nik

Matrix Factorizations: Singular Value Decomposition Presented by Nik Clark MTH 421

Introduction • In the exciting world of numerical analysis, one may wonder “Why? Why do I study matrices and their factorizations? ” • Such a simple answer, “Because matrices and their decompositions can take you anywhere!”

Matrix Decompositions Some interesting ways to decompose a matrix • • • Choleski Jordan LU Polar Proper Orthogonal • • QR Schur Singular Value Spectral (Eigendecomposition)

Singular Value Decomposition We’d like to more formally introduce you to Singular Value Decomposition (SVD) and some of its applications.

What is SVD? • SVD is a type of factorization for a rectangular, real or complex, matrix. • THEOREM: All matrices Amxn have a singular value decomposition.

Why should we care? • All math is awesome. • Also because SVD can be applied to several situations: – Data Compression – Analyzing DNA Gene Expression Data – Solving Least Squares Problems – Information Retrieval

More Caring – Image Processing • De-blurring – Seismology – Digital Signal Processing • Noise Reduction – Data Hiding • Cryptography • Watermarks – Researching Databases

Back to the SVD • Each mxn matrix A decomposes into the product of three matrices A=UΣVT • U is orthogonal and mxm. Its columns span col(A). • V is also orthogonal, but is nxn. Its columns span row(A) • is a diagonal matrix where the singular values of A are along the main diagonal, and all other values are zero.

More on SVD • The m columns of matrix U are the eigenvectors of AAT • The n columns of matrix V are the eigenvectors of ATA • The entries of the main diagonal of matrix are the singular values of A, denoted by i

Another Way to Write • An additional way to write A, apart from A=UΣVT : A = 1 u 1 v. T 1 + 2 u 2 v. T 2 + …+ rurv. Tr , Where r = rank(A), and is defined to be the number of linearly independent columns of A.

Importance • Each term of the expansion is already in order of importance. • 1 ≥ 2 ≥ … ≥ k ≥ 0

Rank k Approximation • Ak=UkΣk. VTk • Where Ak is the first k terms of the SVD factorization of A • i. e. A = 1 u 1 v. T 1 + 2 u 2 v. T 2 + …+ kukv. Tk

More on Rank • A = 1 u 1 v. T 1 + 2 u 2 v. T 2 + …+ kukv. Tk • Where each term of the expansion is a rank 1 matrix.

An Example: Code breaking • Cipher- a method for encrypting a message. • Cryptography – The art of creating a coded message using a cipher. • Cryptanalysis – The art of breaking a code by finding its weakness. • Cryptology – the study of the aforementioned definitions.

How do we decode the code? • Most commonly, a cryptogram is created by substituting one letter for another. • When decoding a code (in english) it is easiest to first decode the vowels. • Vowel pairs are less frequent than consonant-vowel pairs. • More frequently, vowels follow consonants, vfc.

vcf • When vowels follow consonants, there is a mathematical proportion: number of vowel pairs number of vowels < number consonant-vowel pairs number of consonants

The matrix • We define matrix A to be a digram frequency of the letter combinations of our text. • aij is the number of times the ith letter is followed by the jth letter. • We define vector wi to equal 1 when the letter is a vowel and 0 otherwise. • Vector ci is defined to equal 1 when the letter is a consonant and 0 otherwise.

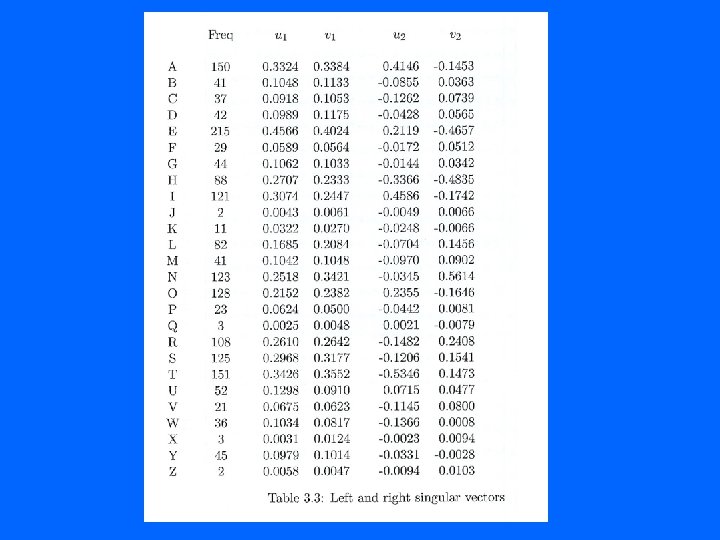
Digram Matrix

Thus • Our vectors w and c are orthogonal. • w. TAw is the number of vowel pairs. • c. TAw is the number of consonant vowel pairs. • We can now rewrite our equation: w. TAw w. TA(w+c) < c. TAw c. TA(w+c)

Singular Vectors • A ~ A 1 = 1 u 1 v. T 1 • f = k 1 * u 1 • f = k 2 * v 1 • Where f represents the frequency of the words in the text.

Digram Matrix

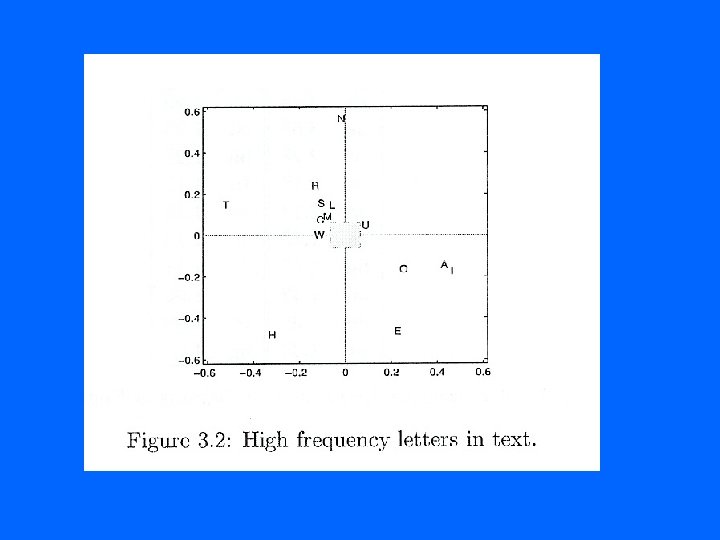
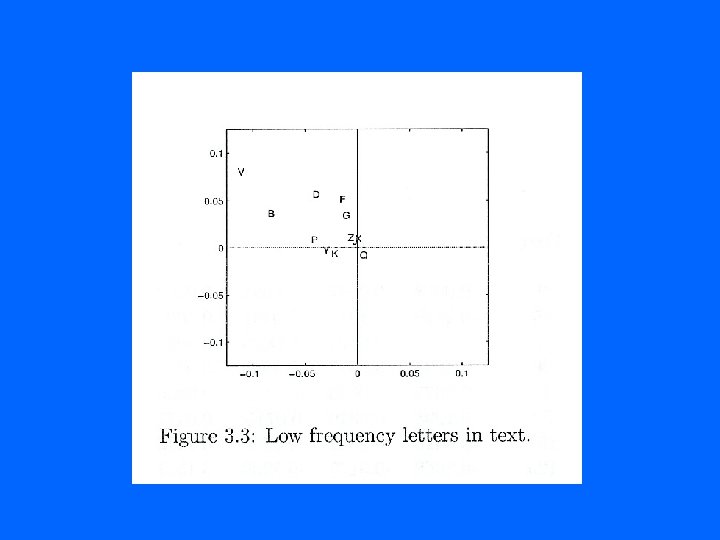
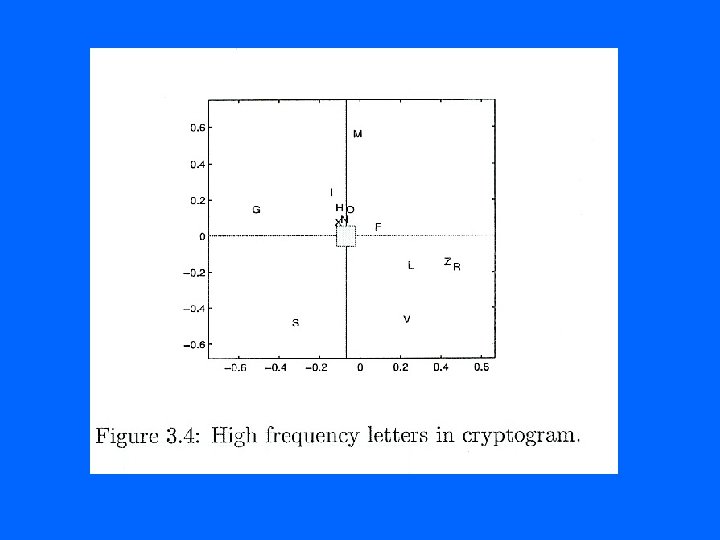
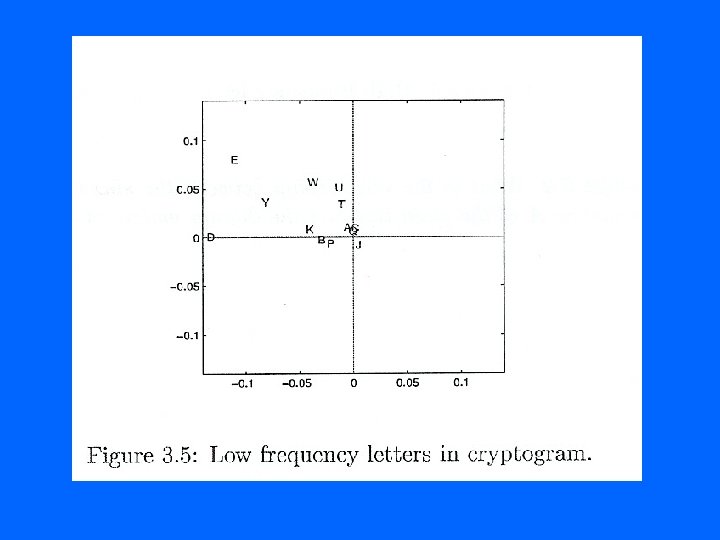
Rank Two • A ~ A 2 = 1 u 1 v. T 1 + 2 u 2 v. T 2 • Rank two is the frequency of vowel pairs. • Each vowel (except for u) corresponds to a (+, -) vector pair. • Each consonant corresponds to a (-, +) vector pair. • There are some exceptions

Neuter Letters • Those letters that correspond to a (+, +) vector pair or a (-, -) vector pair are called neuter. • These letter patterns correspond to any text we consider.

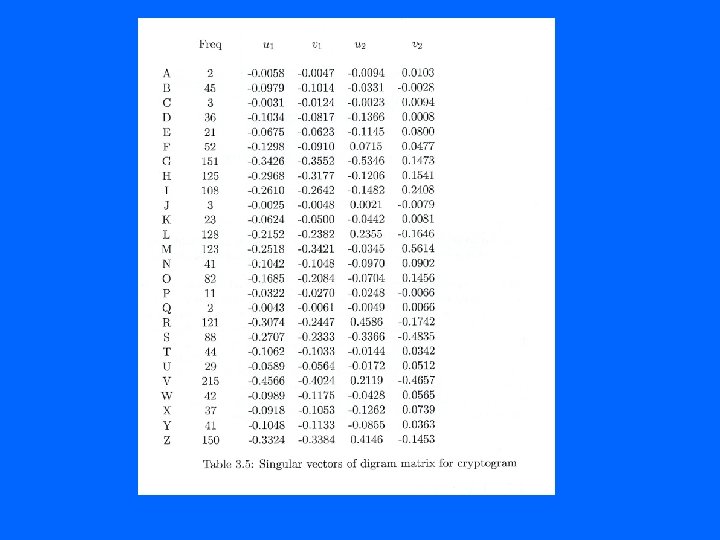
An Encrypted Example • The following matrix is the digram matrix of an encrypted text (cryptogram) similar to the sentence below. • What does this mean? ? • Gsviv rh ml zkkorw nzgsvnzgrxk ru gsviv rh ml nzgsvnzgrxh gl zkkob