MATRIKS Setelah menyaksikan tayangan ini anda dapat menentukan















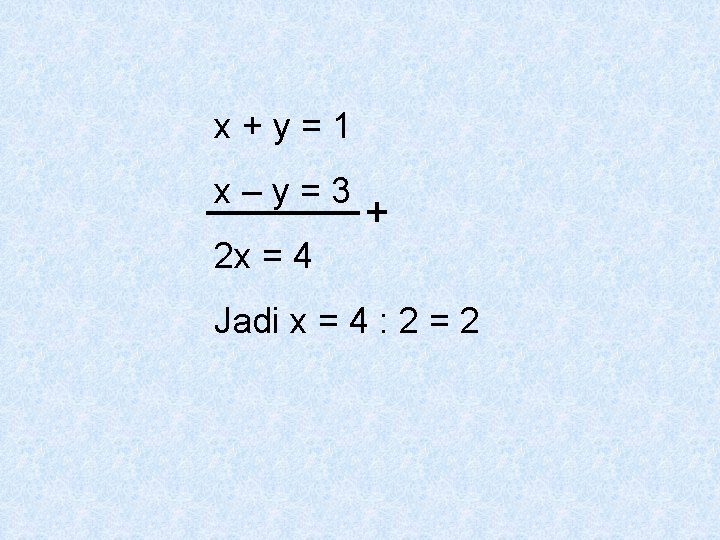








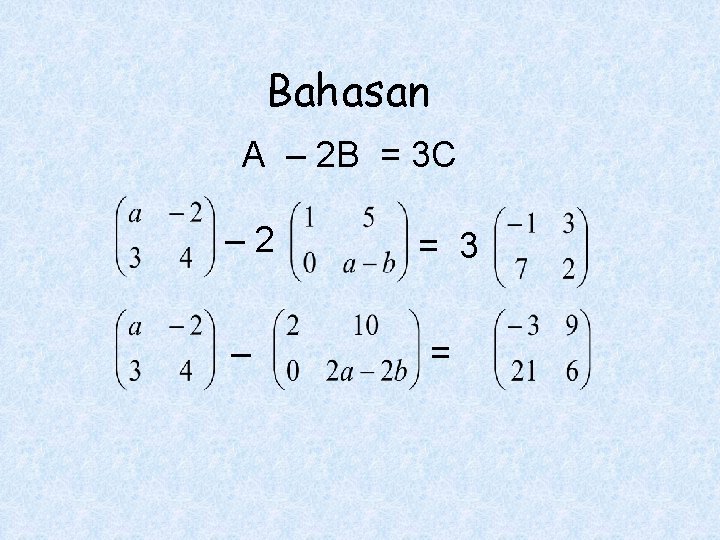






- Slides: 38

MATRIKS

Setelah menyaksikan tayangan ini anda dapat menentukan penyelesaian suatu persamaan matrik dengan menggunakan sifat dan operasi matrik

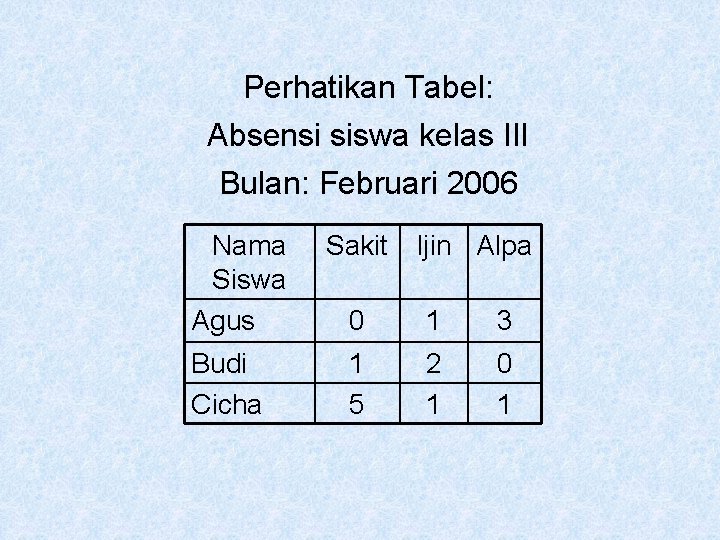
Perhatikan Tabel: Absensi siswa kelas III Bulan: Februari 2006 Nama Siswa Agus Budi Cicha Sakit Ijin Alpa 0 1 3 1 5 2 1 0 1

Jika judul baris dan kolom dihilangkan Nama Siswa Agus Budi Cicha Sakit Ijin Alpa 0 1 5 1 2 1 3 0 1 Judul baris Judul kolom

Maka terbentuk susunan bilangan sebagai berikut: 0 1 3 1 2 0 5 1 1 disebut matriks

Matriks adalah Susunan bilangan berbentuk persegipanjang yang diatur dalam baris dan kolom, ditulis diantara kurung kecil atau siku

Bilangan yang disusun disebut elemen. Banyak baris x banyak kolom disebut ordo matriks. Sebuah matriks ditulis dengan huruf besar

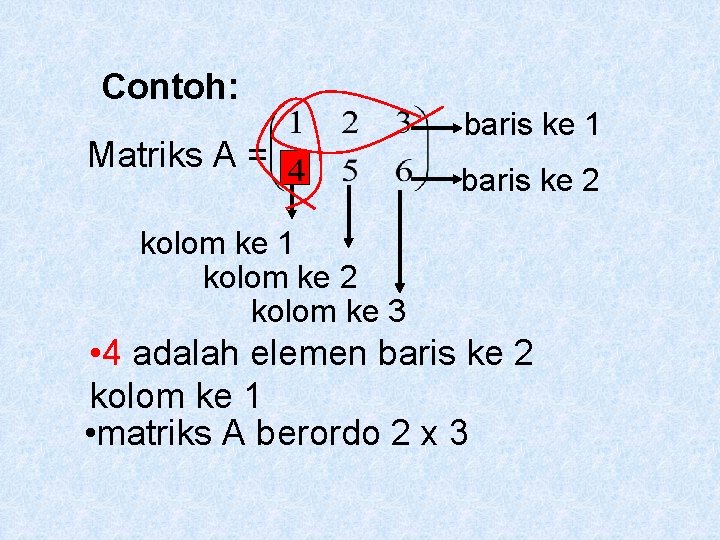
Contoh: Matriks A = baris ke 1 baris ke 2 kolom ke 1 kolom ke 2 kolom ke 3 • 4 adalah elemen baris ke 2 kolom ke 1 • matriks A berordo 2 x 3

Matriks persegi Adalah matriks yang banyak baris dan kolom sama

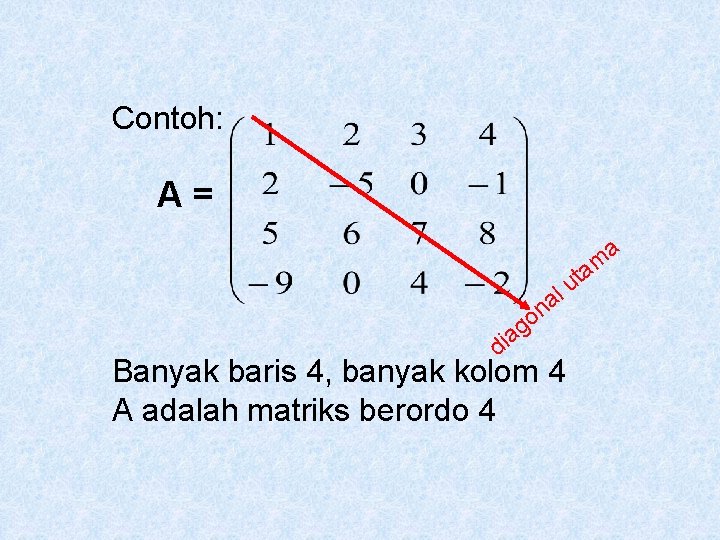
Contoh: A= t u l a n o g a di Banyak baris 4, banyak kolom 4 A adalah matriks berordo 4 a m a

Perhatikan matriks berikut: A= A adalah matriks segitiga atas yaitu matriks yang elemen-elemen di bawah diagonal utamanya bernilai nol

Perhatikan matriks berikut: B= B adalah matriks segitiga bawah yaitu matriks yang elemen-elemen di atas diagonal utamanya bernilai nol

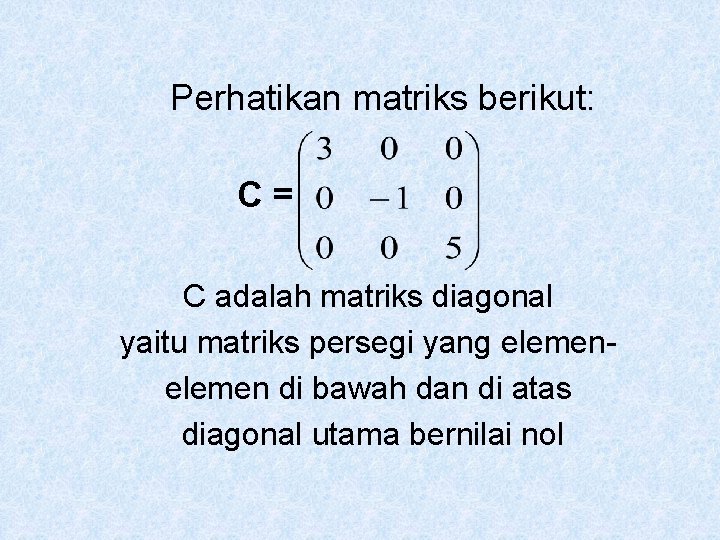
Perhatikan matriks berikut: C= C adalah matriks diagonal yaitu matriks persegi yang elemen di bawah dan di atas diagonal utama bernilai nol

Perhatikan matriks berikut: I= I adalah matriks Identitas yaitu matriks diagonal yang elemen-elemen pada diagonal utama bernilai satu

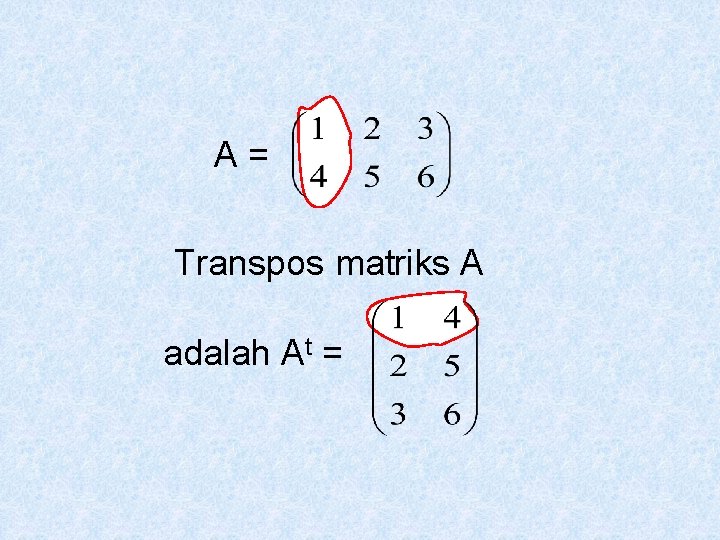
Transpos Matriks Transpos matriks A, ditulis At adalah matriks baru dimana elemen baris matriks At merupakan kolom matriks A

A= Transpos matriks A adalah At =

Kesamaan Dua Matriks matriks A = matriks B jika Ø ordo matriks A = ordo matriks B Øelemen yang seletak sama

A= dan B = Jika matriks A = matriks B, maka x – 7 = 6 x = 13 2 y = -1 y = -½

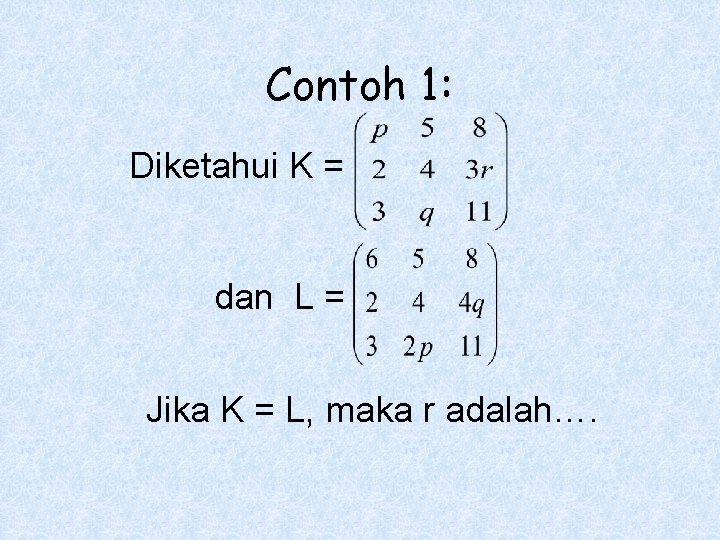
Contoh 1: Diketahui K = dan L = Jika K = L, maka r adalah….

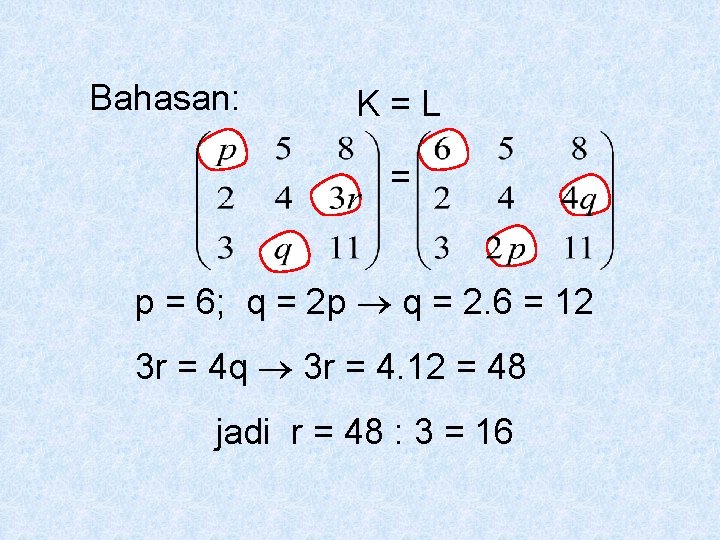
Bahasan: K=L = p = 6; q = 2 p q = 2. 6 = 12 3 r = 4 q 3 r = 4. 12 = 48 jadi r = 48 : 3 = 16

Contoh 2: Misalkan A = dan B = Jika At adalah transpos matriks A maka persamaan At = B dipenuhi bila x = ….

Bahasan: A= At = B =
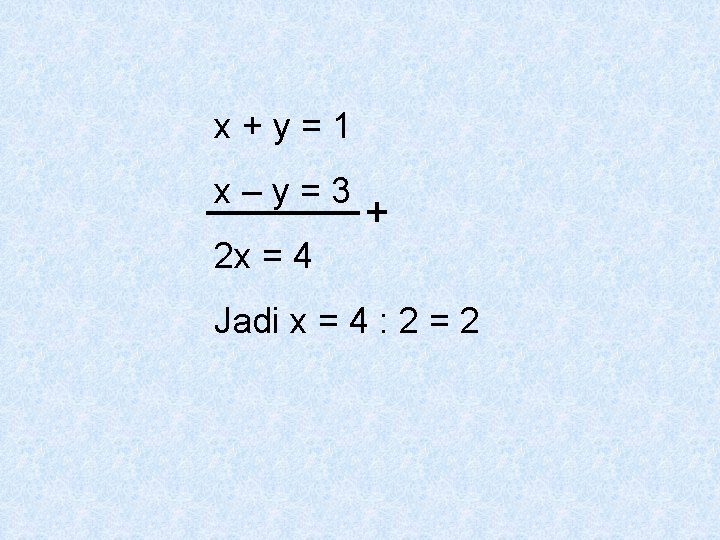
x+y=1 x–y=3 2 x = 4 Jadi x = 4 : 2 = 2

Operasi Pada Matriks ØPenjumlahan ØPengurangan ØPerkalian: perkalian skalar dengan matriks perkalian matriks dengan matriks

Penjumlahan/pengurangan Matriks A dan B dapat dijumlahkan/dikurangkan, jika ordonya sama. Hasilnya merupakan jumlah/selisih elemen-elemen yang seletak

Contoh 1: A= dan B = A + B = + =

Contoh 2: Jika A = , B= dan C = Maka (A + C) – (A + B) =….


Perkalian skalar dengan matriks Jika k suatu bilangan (skalar) maka perkalian k dengan matriks A ditulis k. A, adalah matriks yang elemennya diperoleh dari hasil kali k dengan setiap elemen matriks A

Contoh 1: Matriks A = Tentukan elemen-elemen matriks 5 A! Jawab: 5 A =

Contoh 2: Matriks A = , B= dan C = Jika A – 2 B = 3 C, maka a + b = ….
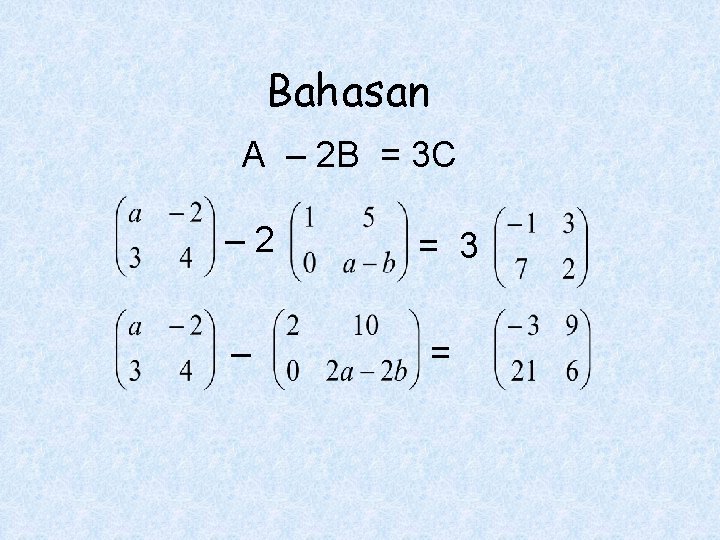
Bahasan A – 2 B = 3 C – 2 = 3 – =



Contoh 3: Matriks A = dan B = Supaya dipenuhi A = 2 Bt, dengan Bt adalah matriks transpos dari B maka nilai m = ….

Bahasan B= berarti Bt = A = 2 Bt =


= 4 = 2 k k = 2 2 l = 4 k + 2 2 l = 4. 2 + 2 2 l = 10 l = 5 3 m = 2 l + 14 3 m = 2. 5 + 14 = 24 Jadi m = 8
 Pembuka surat lamaran pekerjaan
Pembuka surat lamaran pekerjaan Cara mengubah matriks menjadi matriks segitiga atas
Cara mengubah matriks menjadi matriks segitiga atas Det a
Det a Setelah mempelajari materi ini
Setelah mempelajari materi ini Setelah mempelajari materi
Setelah mempelajari materi Setelah mempelajari materi ini
Setelah mempelajari materi ini Setelah mempelajari materi ini
Setelah mempelajari materi ini Tahapan pengolahan bahan pangan buah buahan menjadi makanan
Tahapan pengolahan bahan pangan buah buahan menjadi makanan Contoh determinan dari matriks
Contoh determinan dari matriks Rank dari sebuah matriks dapat dihasilkan dari
Rank dari sebuah matriks dapat dihasilkan dari Operasi pengurangan vektor menggunakan aturan segitiga
Operasi pengurangan vektor menggunakan aturan segitiga P hari ini hujan q hari ini anginnya kencang
P hari ini hujan q hari ini anginnya kencang Hkey_dyn_data
Hkey_dyn_data Dengan ini atau bersama ini
Dengan ini atau bersama ini Prueba cronometrada de levantate y anda
Prueba cronometrada de levantate y anda Pengertian mad ta'zim
Pengertian mad ta'zim Stephanie de anda
Stephanie de anda Velad y orad porque vuestro adversario el diablo
Velad y orad porque vuestro adversario el diablo Todo tiene su tiempo y todo lo que se quiere
Todo tiene su tiempo y todo lo que se quiere Rumus koefisien restitusi pantulan bola
Rumus koefisien restitusi pantulan bola Panggilan hidup berkeluarga adalah
Panggilan hidup berkeluarga adalah Anda ungureanu
Anda ungureanu Jika anda diberi 3 buah pil oleh dokter
Jika anda diberi 3 buah pil oleh dokter Contoh ayat kesimpulan
Contoh ayat kesimpulan Apa yang anda ketahui tentang evaluasi
Apa yang anda ketahui tentang evaluasi Bangkit ketika anda jatuh
Bangkit ketika anda jatuh Seberapa penting keilmuan keselamatan kerja menurut anda
Seberapa penting keilmuan keselamatan kerja menurut anda Socili
Socili Prinsip dasar jaringan adalah
Prinsip dasar jaringan adalah Anda al
Anda al Difference between nda and anda slideshare
Difference between nda and anda slideshare Apa itu ayat aktif dan pasif
Apa itu ayat aktif dan pasif Menurut anda apa tujuan dari dimensional modelling....?
Menurut anda apa tujuan dari dimensional modelling....? Jika anda diberi 3 buah pil oleh dokter
Jika anda diberi 3 buah pil oleh dokter Ketika anda memeras ujung kantong plastik
Ketika anda memeras ujung kantong plastik Sebutkan contoh koloid pelindung yang anda ketahui
Sebutkan contoh koloid pelindung yang anda ketahui Gkata
Gkata Bayangkan anda seorang penumpang taksi
Bayangkan anda seorang penumpang taksi Anda telecom
Anda telecom






























































