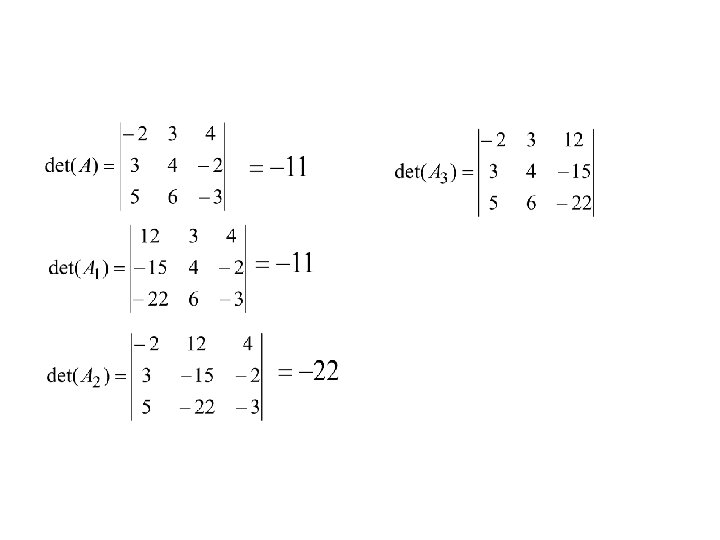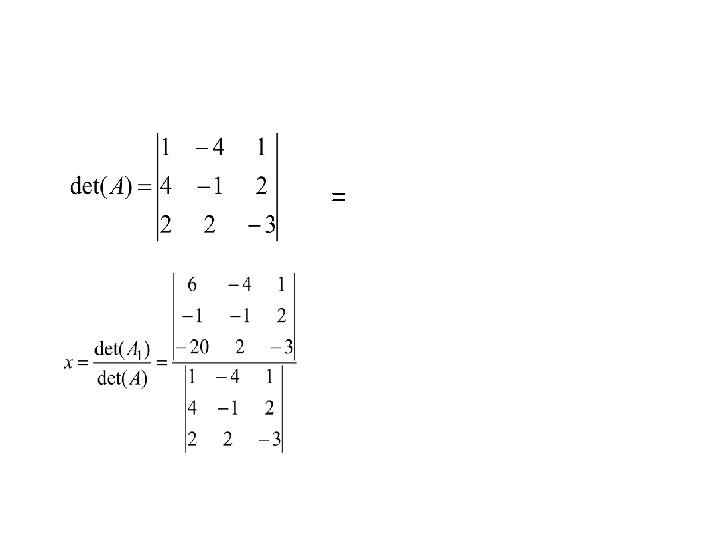MATRIKS NOTASI MATRIKS q Matriks yang mempunyai m






















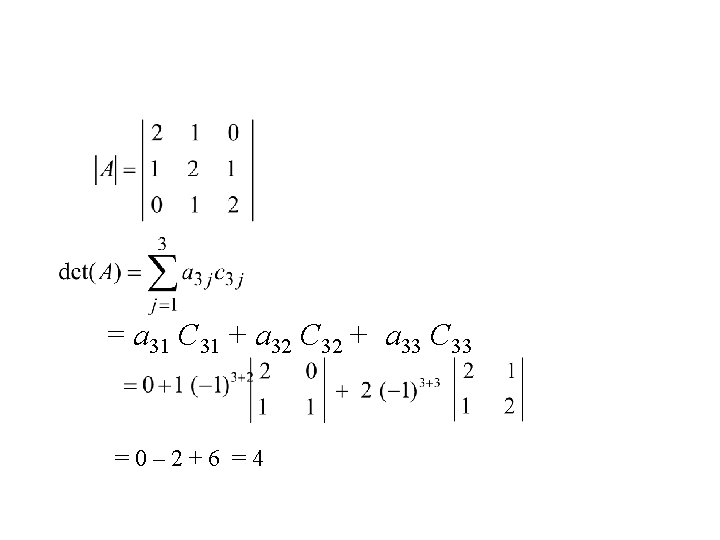








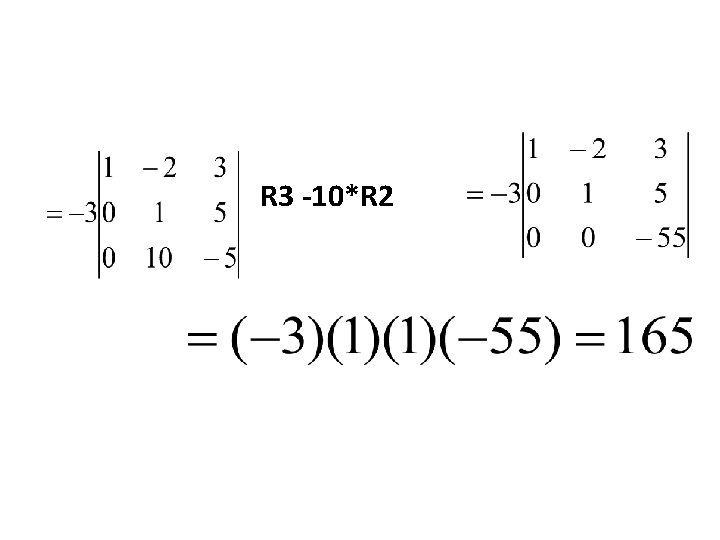




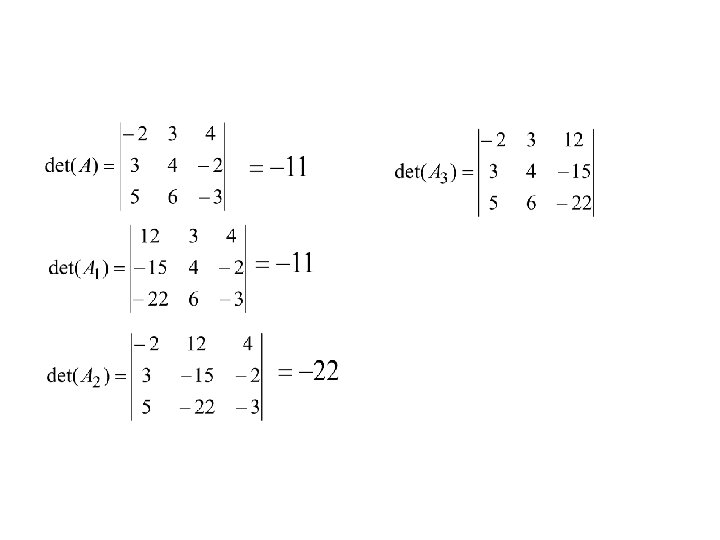


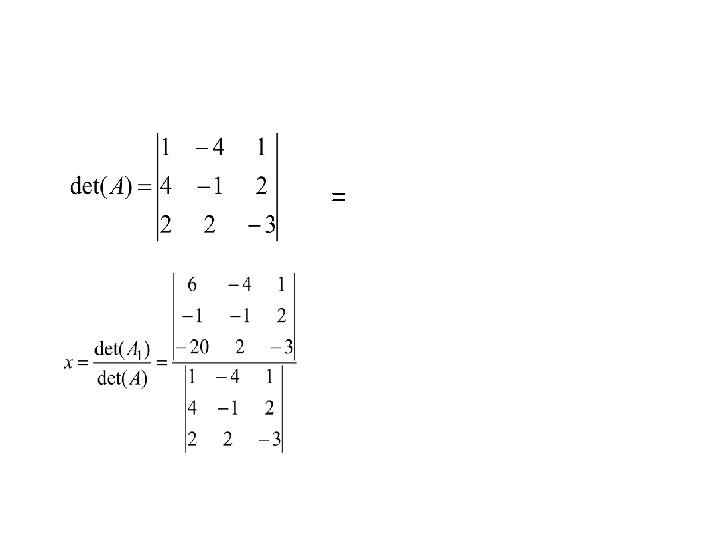

- Slides: 45

MATRIKS

NOTASI MATRIKS q Matriks yang mempunyai m baris dan n kolom disebut matriks berordo atau berukuran m x n. Notasi A = (aij) q Memudahkan menunjuk anggota suatu matriks Dengan i = 1, 2, . . . , m j = 1, 2, . . . , n A= 2

JENIS –JENIS MATRIKS q Matriks persegi adalah matriks yang berukuran n x n q Matriks nol adalah matriks yang setiap entri atau elemennya adalah bilangan nol 3

JENIS –JENIS MATRIKS q Matriks Diagonal adalah matriks persegi yang semua elemen diatas dan dibawah diagonalnya adalah nol. Dinotasikan sebagai D. Contoh : q Matriks Skalar adalah matriks diagonal yang semua elemen pada diagonalnya sama 4

JENIS –JENIS MATRIKS q Matriks Identitas adalah matriks skalar yang elemen-elemen pada diagonal utamanya bernilai 1. q Matriks Segitiga Atas adalah matriks persegi yang elemen di bawah diagonal utamanya bernilai nol q Matriks Segitiga Bawah adalah matriks persegi yang elemen di atas diagonal utamanya bernilai nol 5

Dua matriks dapat dijumlahkan jika mempunyai ukuran yang sama. contoh

• Dua matriks dapat dikalikan jika banyaknya kolom pada matriks pertama sama dengan banyak baris pada matriks kedua. • Contoh

DETERMINAN MATRIKS q Setiap matriks persegi memiliki nilai determinan q Nilai determinan dari suatu matriks merupakan suatu skalar. q Jika nilai determinan suatu matriks sama dengan nol, maka matriks tersebut disebut matriks singular. 8

NOTASI DETERMINAN q Misalkan matriks A merupakan sebuah matriks persegi Determinan A ditulis sebagai det (A) det(A) sering dinotasikan |A| Ada beberapa cara untuk menentukan determinan, diantaranya adalah: Determinan dengan cara Sarrus Determinan dengan cara Ekspansi Kofaktor Determinan dengan cara Operasi Baris Elementer (OBE) 9

NOTASI DETERMINAN q Pada matriks 2 x 2 cara determinannya adalah : q Contoh : 10 menghitung nilai

METODE SARRUS q Pada matriks 3 x 3 cara menghitung nilai determinannya adalah menggunakan Metode Sarrus q Metode Sarrus hanya untuk matrix berdimensi 3 x 3 11

Contoh : Tentukan determinan matriks Jawab : =1

METODE SARRUS q Nilai Determinan dicari menggunakan metode Sarrus det(B) = (-2· 1 ·-1) + (2 · 3 · 2) + (-3 ·-1 · 0) – (-3 · 1 · 2) –(-2 · 3 · 0)-(2 ·-1) = 2 +12+0+6 -0 -2 = 18 13

MINOR q Yang dimaksud dengan MINOR unsur aij adalah determinan yang berasal dari determinan orde n dikurangi dengan baris ke-i dan kolom ke-j. q Dinotasikan dengan Mij q Contoh Minor dari elemen a₁₁ 14

MINOR q Minor-minor dari Matrik A (ordo 3 x 3) 15

KOFAKTOR MATRIKS q Kofaktor dari baris ke-i dan kolom ke-j dituliskan dengan q Contoh : Kofaktor dari elemen a 23 16

TEOREMA LAPLACE q Determinan dari suatu matriks sama dengan jumlah perkalian elemen-elemen dari sembarang baris atau kolom dengan kofaktor-kofaktornya 17

TEOREMA LAPLACE Determinan dengan Ekspansi Kofaktor Pada Baris q Misalkan ada sebuah matriks A berordo 3 x 3 q Determinan Matriks A dengan metode ekspansi kofaktor baris pertama |A| 18

TEOREMA LAPLACE q Determinan Matriks A dengan metode ekspansi kofaktor baris kedua |A| q Determinan Matriks A dengan metode ekspansi kofaktor baris ketiga |A| 19

TEOREMA LAPLACE Determinan dengan Ekspansi Kofaktor Pada Kolom q Misalkan ada sebuah matriks A berordo 3 x 3 q Determinan Matriks A dengan metode ekspansi kofaktor kolom pertama |A| 20

TEOREMA LAPLACE q Determinan Matriks A dengan metode ekspansi kofaktor kolom kedua |A| q Determinan Matriks A dengan metode ekspansi kofaktor kolom ketiga |A| 21

Contoh Hitunglah Det(A) dengan ekspansi kofaktor : Misalkan, kita akan menghitung det (A) dengan ekspansi kofaktor sepanjang baris ke-3
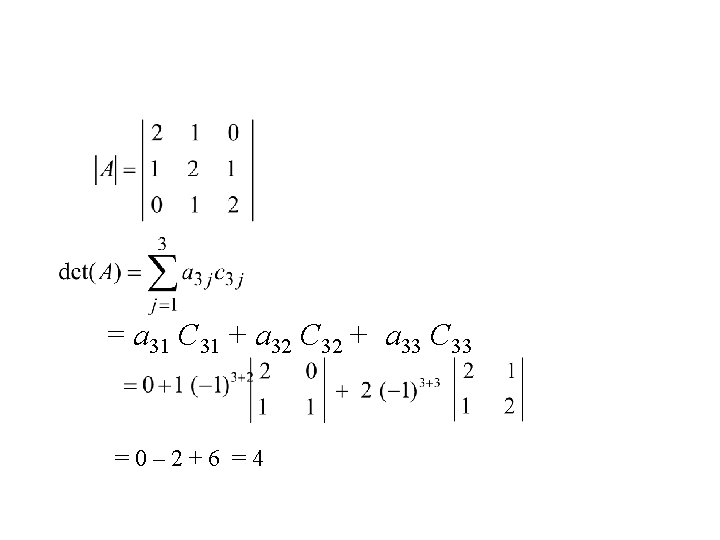
= a 31 C 31 + a 32 C 32 + a 33 C 33 =0– 2+6 =4

Menghitung det (A) dengan ekspansi kofaktor sepanjang kolom ke-3 =0– 2+6 =4

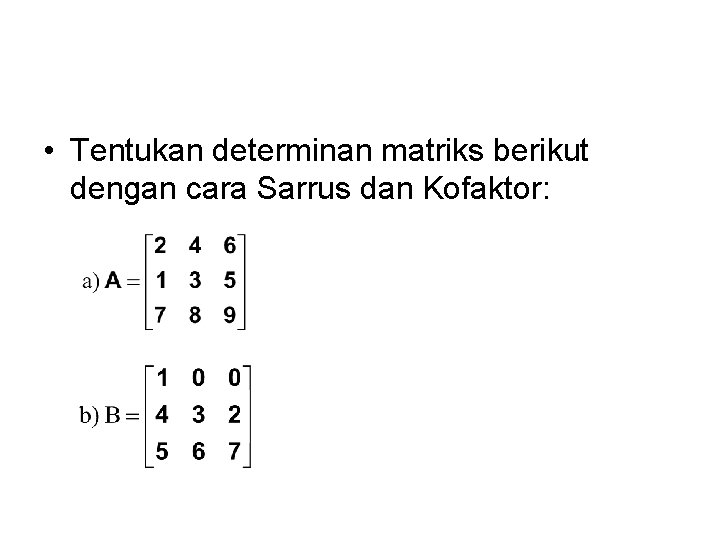
• Tentukan determinan matriks berikut dengan cara Sarrus dan Kofaktor:

Penyelesaian maka det (A) = 2. 3. 9 + 4. 5. 7 + 6. 1. 8 – 6. 3. 7 – 2. 5. 8 – 4. 1. 9 = 54 + 140 + 48 – 126 – 80 – 36

Dengan ekspansi kofaktor = 2. (27 – 40) – (36 – 48) + 7. (20 – 18) = - 26 + 12+ 14 = 0

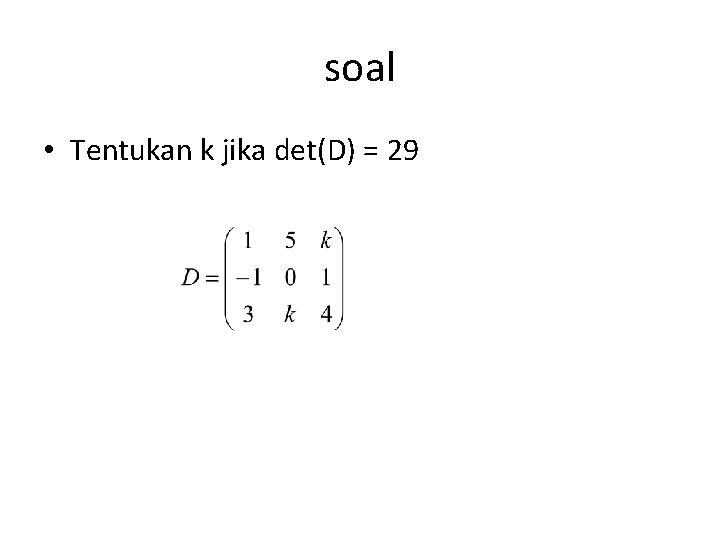
soal • Tentukan k jika det(D) = 29

Sifat-sifat determinan • Nilai determinan tidak berubah apabila baris dan kolomnya dipertukarkan. Jadi, Contoh: • Jika semua unsur dari suatu baris (atau kolom) adalah nol, determinan matriks itu sama dengan nol.

• Jika semua unsur dari suatu baris (atau kolom) adalah nol, kecuali satu unsur, determinannya sama dengan hasil kali unsur itu dengan kofaktornya. • Pertukaran dua baris atau dua kolom sembarang akan mengubah tanda determinan.

• Jika semua unsur dalam suatu baris (atau kolom) dikalikan dengan sebuah bilangan, determinannya juga dikalikan dengan bilangan itu. • Jika dua baris (atau kolom) sama atau sebanding, determinannya sama dengan nol.

• Jika kita mengalikan unsur-unsur suatu baris (atau kolom) dengan sebuah bilangan kemudian dijumlahkan dengan unsur-unsur yang bersesuaian dengan suatu baris (atau kolom) yang lain, nilai determinannya tetap. • Jika A dan B dua matriks persegi yang berukuran sama, maka det(AB) = det(A). det(B)

Menentukan Determinan dengan cara OBE Tentukan det(A) Pertukarkan R 1 dengan R 2 det(B)=-det(A)

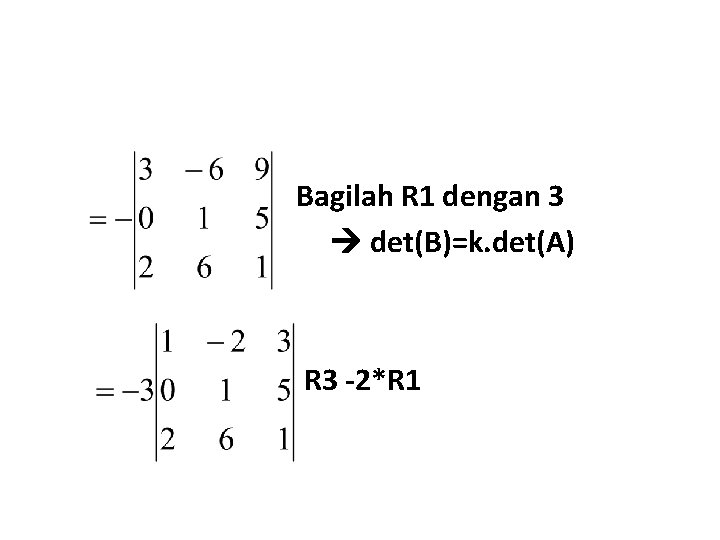
Bagilah R 1 dengan 3 det(B)=k. det(A) R 3 -2*R 1
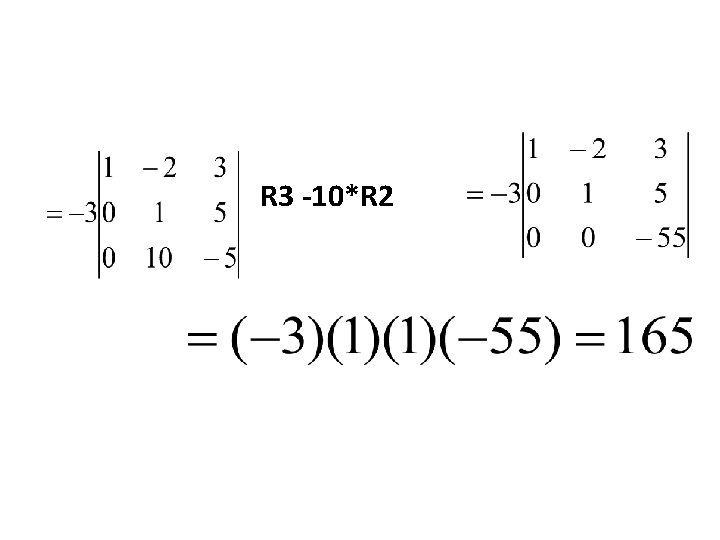
R 3 -10*R 2

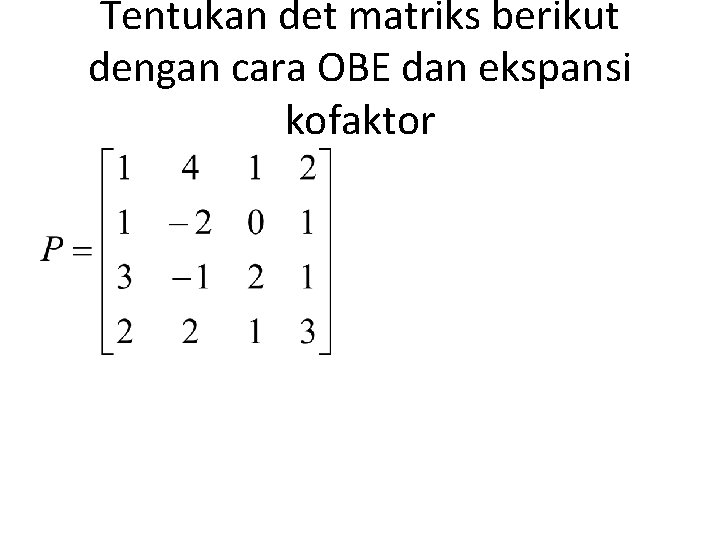
Tentukan det matriks berikut dengan cara OBE dan ekspansi kofaktor

Aturan Cramer • Untuk mencari solusi dari SPL (Sistem Persamaan Linear) tertentu (matriks nxn) • Teorema : Jika Ax=b merupakan suatu sistem n persamaan linier dalam n peubah sedemikian sehingga det(A) ≠ 0, maka sistem tersebut mempunyai penyelesaian yang unik (tunggal).

Sistem Persamaan Linear

. . . dengan Aj adalah matriks yang diperoleh dengan menggantikan anggota kolom ke j dari A dengan anggota matriks b

• Tentukan penyelesaian dari SPL berikut dengan menggunakan aturan cramer 1) -2 x + 3 y + 4 z = 12 3 x + 4 y – 2 z =-15 5 x + 6 y – 3 z =-22 2) X 1 + 2 X 3 = 6 -3 X 1 + 4 X 2 + 6 X 3 = 30 -X 1 – 2 X 2 + 3 X 3 = 8