MATRIKS Macam Matriks 1 2 3 4 5

MATRIKS

Macam Matriks 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Matriks Baris Matriks kolom Matriks Nol Matriks Bujur Sangkar Matriks Diagonal Matriks Satuan (I) Matriks Skalar Matriks Segitiga Atas Matriks Segitiga Bawah Matriks Simetris 11. Matriks Simetri Skew 1. aij = -aji, dan diagonalnya nol 12. Matriks Tridiagonal 13. Matriks Transpose 14. Matriks Ortogonal 1. Matriks bujur sangkar yg memenuhi [A][A]T = [A]T[A]=[ I ]

Determinants • Determinants are useful in eigenvalue problems and differential equations. • Can be found only for square matrices. • Simple example: 2 nd order determinant

3 rd order determinant • The determinant of a 3 X 3 matrix is found as follows: • The terms on the RHS can be evaluated as shown for a 2 nd order determinant.

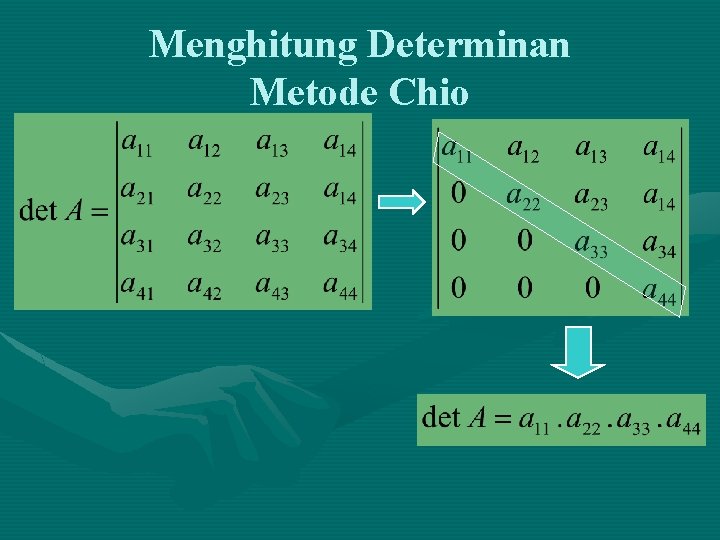
Menghitung Determinan Metode Chio

Sifat-Sifat (Metode Chio) • Bila semua unsur dari suatu baris/kolom = nol, determinan = nol. • Harga determinan tidak berubah bila semua unsur baris diubah menjadi unsur kolom dan semua kolom menjadi baris. • Pertukaran tempat antara baris dengan baris atau antara kolom dengan kolom akan mengubah tanda determinan • Bila unsur-unsur baris/kolom dikalikan suatu faktor, maka determinan harus dikalikan juga. • Bila suatu matriks ada dua baris/ dua kolom yg identik maka determinannya = nol • Tanpa mengubah harga determinan semua unsur sebarang baris/kolom dapat dikalikan dgn sebuah faktor dan menambahkan atau mengurangkan dari sebarang baris/kolom

Some theorems for determinants • Cramer’s: If the determinant of a system of n equations with n unknowns is nonzero, that system has precisely one solution. • det(AB)=det(BA)=det(A)det(B)

Menghitung Determinan Minor dan Kofaktor Penghitungan Determinan berdasar Ekspansi Baris ke-1

Rank (Tingkat) Matriks • Jika det matriks ≠ 0, maka rank r = orde matriks (n). • Jika det matriks = 0, maka harus dilihat minor dari matrik tsb. Jika matriks bujursangkar di dalam determinan ≠ 0, maka rank =2. • Matriks bujur sangkar orde n dengan rank = n (det A≠ 0) disebut matiks non-singular. • Matriks zero memiliki rank = 0.

Contoh Rank Matriks

Matrix rank • The rank of a matrix is simply the number of independent row vectors in that matrix. • The transpose of a matrix has the same rank as the original matrix. • To find the rank of a matrix by hand, use Gauss elimination and the linearly dependant row vectors will fall out, leaving only the linearly independent vectors, the number of which is the rank.

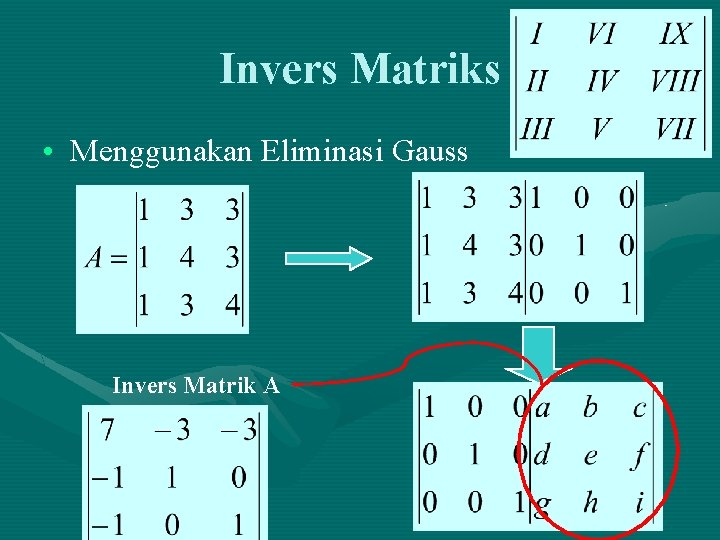
Invers Matriks • Menggunakan Eliminasi Gauss Invers Matrik A

Penggunaan Matriks Penyelesaian Persamaan Linier • Metode Cramer • Metode Gauss Seidel • Menggunakan Invers Matriks – Ax=b. maka x=A-1 b • Metode Gauss

Sistem Persamaan Linier Homogen