Matriks dan Transformasi Linier Dra Dwi Achadiani M

Matriks dan Transformasi Linier Dra. Dwi Achadiani, M. Kom

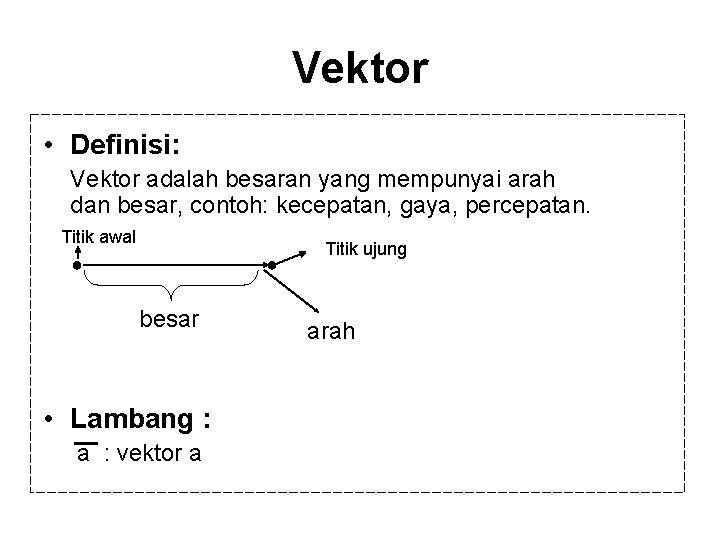
Vektor • Definisi: Vektor adalah besaran yang mempunyai arah dan besar, contoh: kecepatan, gaya, percepatan. Titik awal ● ● besar • Lambang : a : vektor a Titik ujung arah

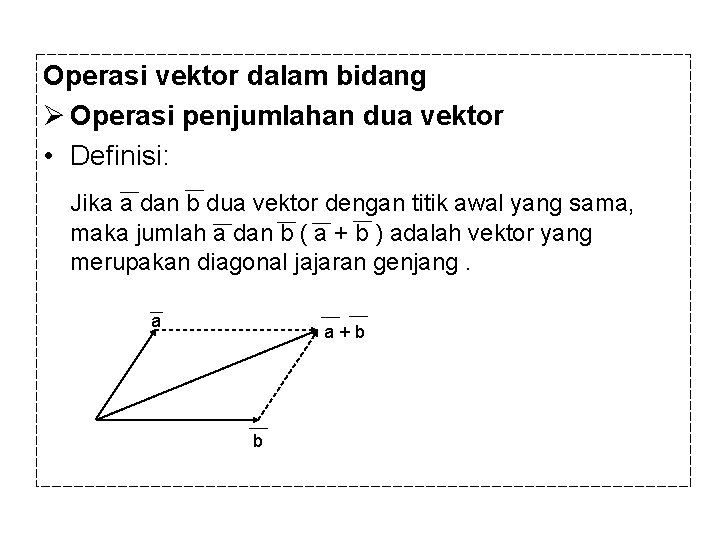
Operasi vektor dalam bidang Ø Operasi penjumlahan dua vektor • Definisi: Jika a dan b dua vektor dengan titik awal yang sama, maka jumlah a dan b ( a + b ) adalah vektor yang merupakan diagonal jajaran genjang. a a+b b

Sifat penjumlahan vektor Ø Operasi perkalian vektor dengan bil riel Sifat perkalian vektor dengan bil riel

Ø Kombinasi Linier

Definisi: Jika adalah vektor-vektor di R²(atau di ), maka: dinamakan kombinasi linier dari Ø Panjang Vektor (Norm) Definisi: Panjang vektor di didefinisikan :

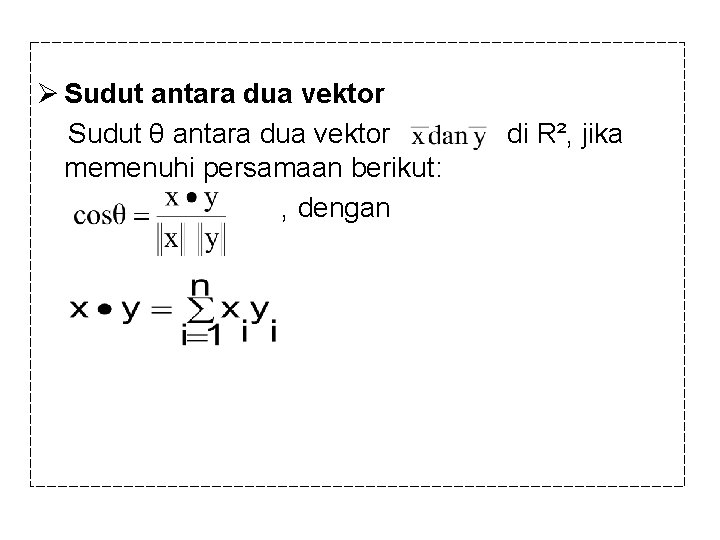
Ø Sudut antara dua vektor Sudut θ antara dua vektor memenuhi persamaan berikut: , dengan di R², jika

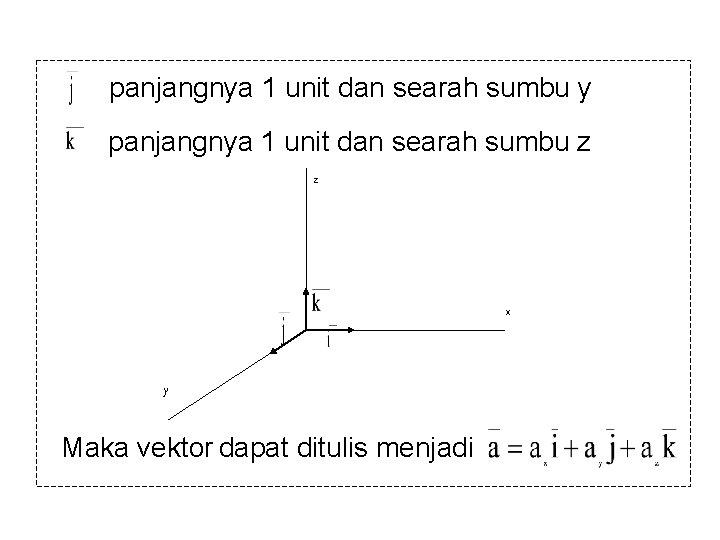
Ø Perkalian Silang Definisi: Jika 2 vektor di , maka: panjangnya 1 unit dan searah sumbu x

panjangnya 1 unit dan searah sumbu y panjangnya 1 unit dan searah sumbu z z x y Maka vektor dapat ditulis menjadi

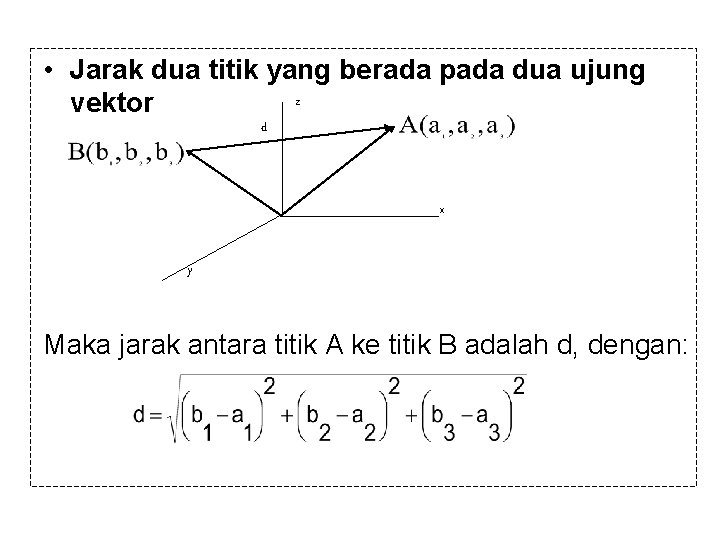
• Jarak dua titik yang berada pada dua ujung z vektor d x y Maka jarak antara titik A ke titik B adalah d, dengan:

Ø Bergantung Linier dan Bebas Linier Vektor- vektor : dengan , apabila tidak semua berharga nol, maka vektor disebut bergantung linier, sedangkan apabila semua berharga nol maka vektor disebut bebas linier.

Ø Vektor pembentuk ruang vektor Definisi: suatu himpunan vektor-vektor disebut sistem pembentuk ruang vektor V, ditulis V= bila setiap dapat ditulis sbg kombinasi linier dari

• Dimensi dan Basis Ø Dimensi Definisi: suatu vektor V dikatakan berdimensi n bila dapat diketemukan suatu himpunan n vektor-vektor V yang bebas linier Atau : maksimum banyaknya vektor-vektor V yang bebas linier.

Ø Basis Definisi: Setiap sistem pembentuk yang bebas linier disebut basis ruang vektor tersebut.

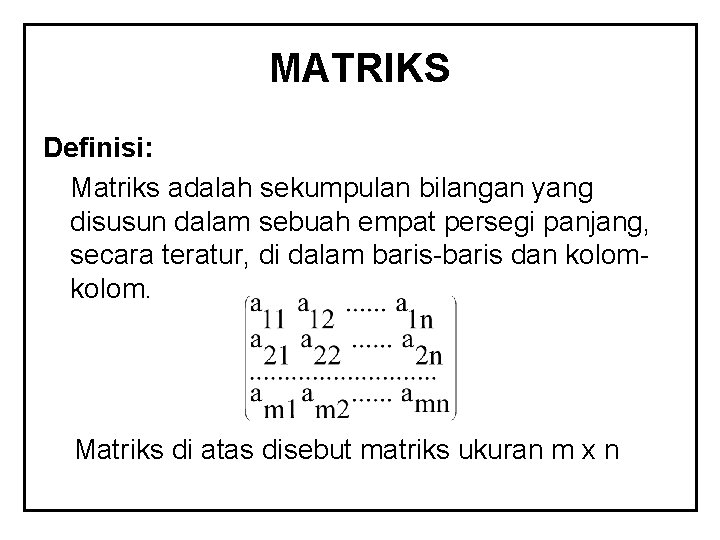
MATRIKS Definisi: Matriks adalah sekumpulan bilangan yang disusun dalam sebuah empat persegi panjang, secara teratur, di dalam baris-baris dan kolom. Matriks di atas disebut matriks ukuran m x n

Ø Operasi Matriks 1. Operasi Kesamaan Dua matriks A dan B disebut sama, jika: a) A dan B sejenis b) Setiap unsur yang seletak sama. A = B, A ≠ C, B ≠ C

2. Penjumlahan dua matriks Definisi: Jumlah dua matriks A dan B yang sejenis adalah sebuah matriks C yang sejenis pula dengan unsur -unsur , dimana terdapat hubungan: .

Sifat-sifat penjumlahan: §Komutatif : A + B = B + A §Assosiatif : A + (B + C) = (A + B) + C 3. Perkalian dengan skalar ( ) Perkalian sebuah matriks dengan skalar ( ) maka setiap unsur matriks tersebut terkalikan dengan skalar ( ). , maka A= .

Sifat-sifat perkalian matriks dengan skalar 1. (A + B) = A + B 2. ( + β ) A = A + β A 3. (β A) = β A

4. Perkalian dua matriks Definisi: Dua matriks A (m x n), dan B (p x q) didefinisikan hasil kalinya, jika n = p , maka hasilkali adalah matriks C (m x q) dengan unsur-unsur:

Catatan: • Perkalian 2 matriks AB dapat didefinisikan, jika banyaknya kolom matriks A = banyaknya baris matriks B. • Hasil kali dua matriks AB adalah suatu matriks dengan banyaknya baris = banyaknya baris matriks A dan banyaknya kolom = banyaknya kolom matriks B. • Pada umumnya AB ≠ BA Contoh: 1 x 3 3 x 1 1 x 1

2 x 2 3 x 3

Ø Macam-macam matriks 1. Matriks bujursangkar Definisi: matriks bujursangkar adalah matriks dimana banyaknya baris = banyaknya kolom 2. Matrik satuan/ matriks identitas • Matriks bujur sangkar • Setiap unsurnya nol, kecuali didiagonal utama = 1

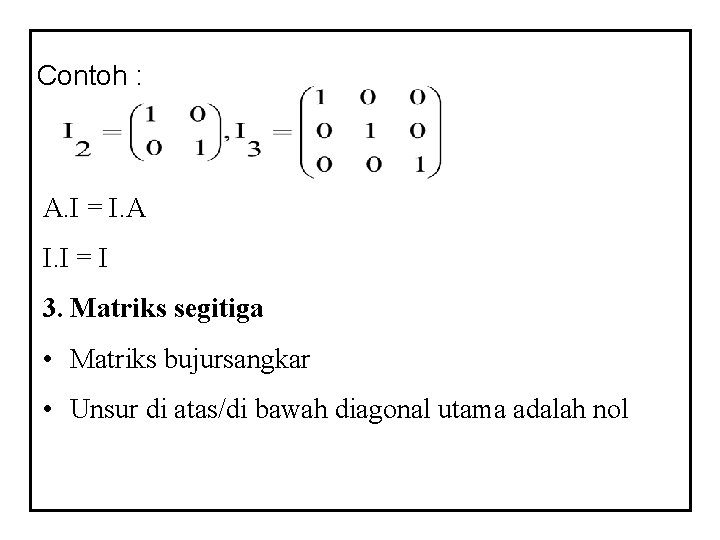
Contoh : A. I = I. A I. I = I 3. Matriks segitiga • Matriks bujursangkar • Unsur di atas/di bawah diagonal utama adalah nol

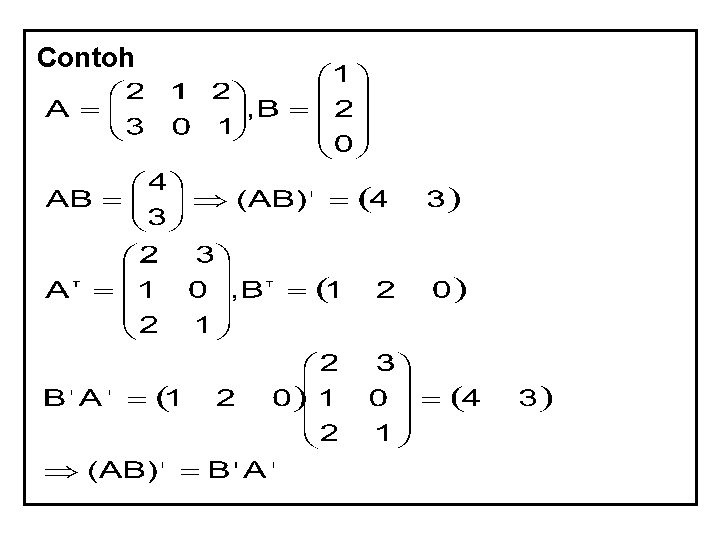
Contoh : 4. Matriks Tranpose • Tidak perlu bujursangkar • Setiap baris ditukar tempat dengan kolom

Contoh :

Sifat-sifat matriks transfose

Contoh

5. Matriks simetris Matriks A disebut simetris apabila • Matriks Bujur sangkar Contoh

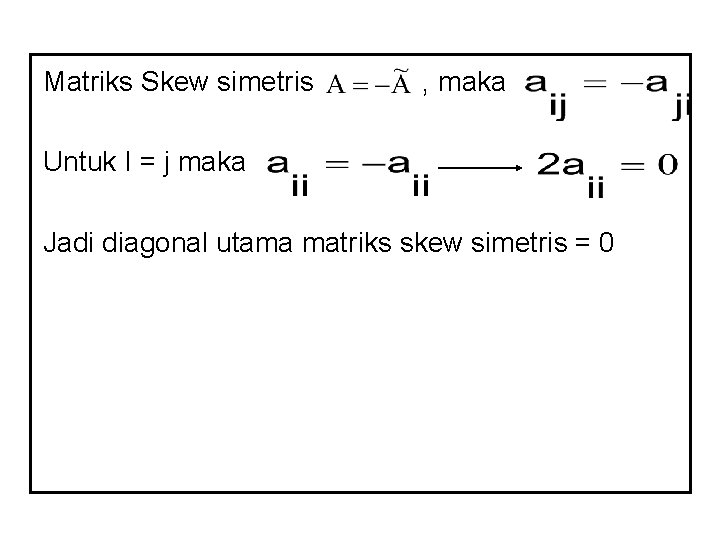
6. Matriks skew simetris Matriks A disebut matriks skew simetri jika • Bujur sangkar Contoh

Matriks Skew simetris , maka Untuk I = j maka Jadi diagonal utama matriks skew simetris = 0

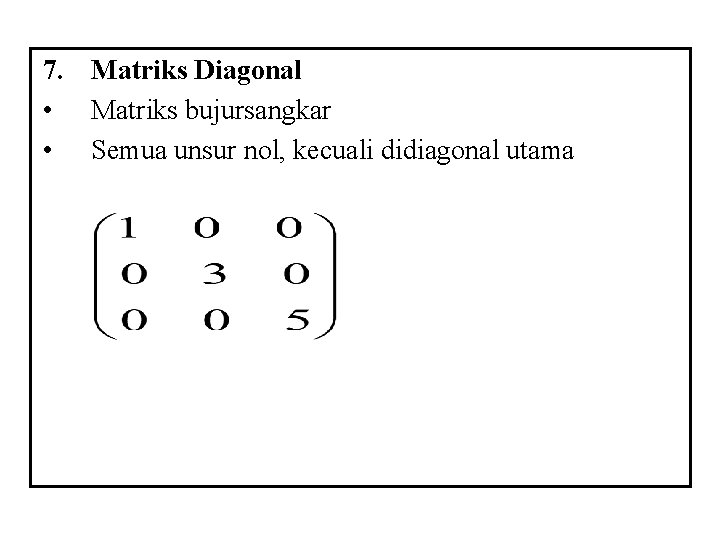
7. Matriks Diagonal • Matriks bujursangkar • Semua unsur nol, kecuali didiagonal utama

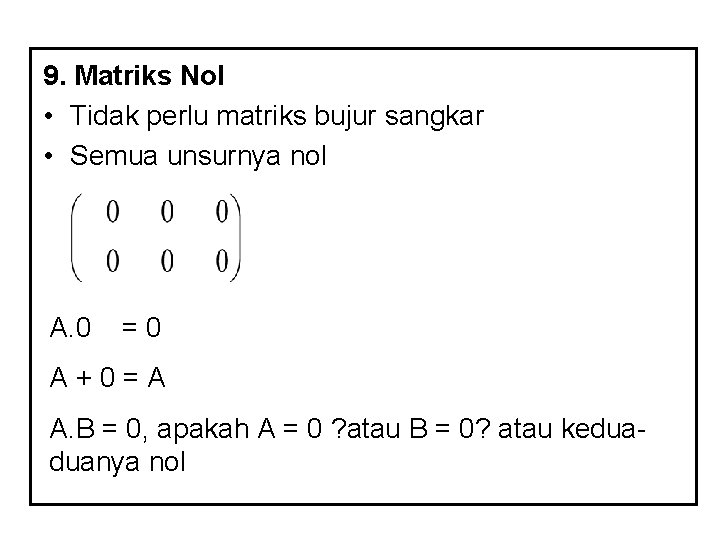
9. Matriks Nol • Tidak perlu matriks bujur sangkar • Semua unsurnya nol A. 0 =0 A+0=A A. B = 0, apakah A = 0 ? atau B = 0? atau keduaduanya nol

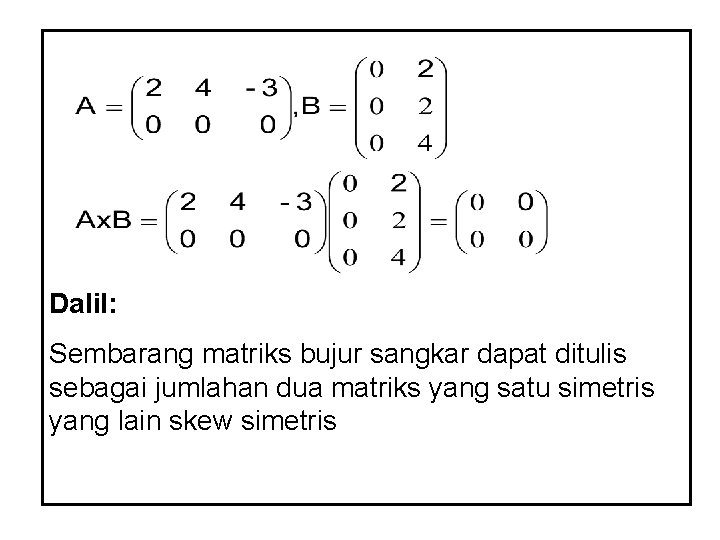
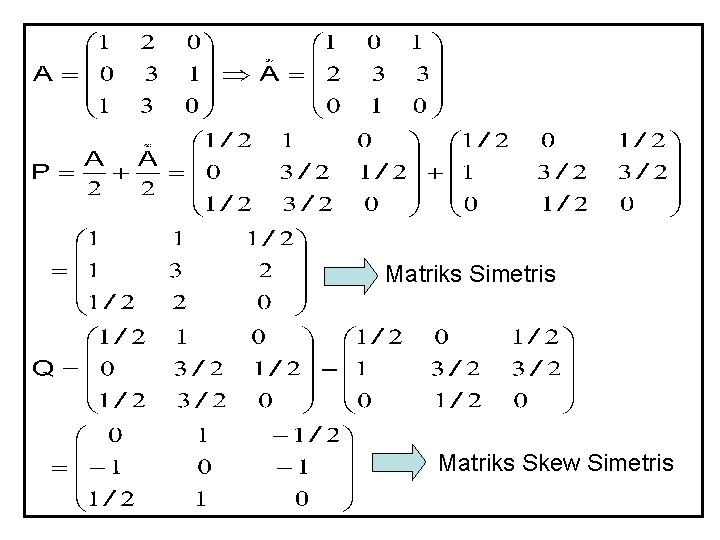
Dalil: Sembarang matriks bujur sangkar dapat ditulis sebagai jumlahan dua matriks yang satu simetris yang lain skew simetris

Bukti:

Matriks Simetris Matriks Skew Simetris

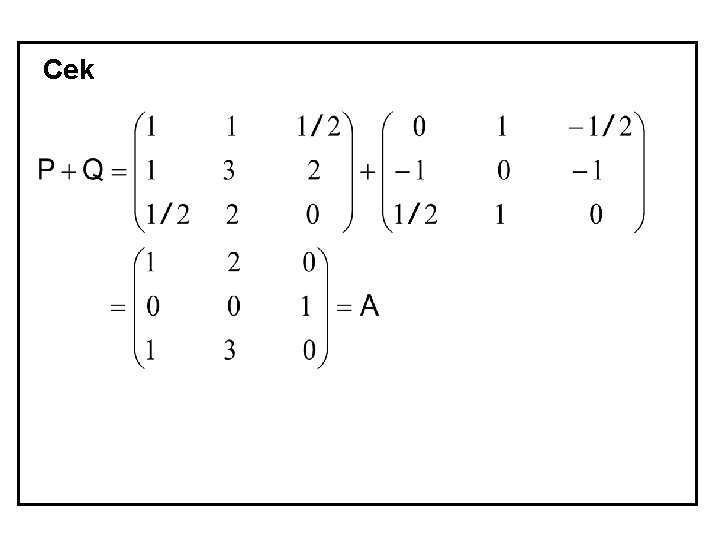
Cek

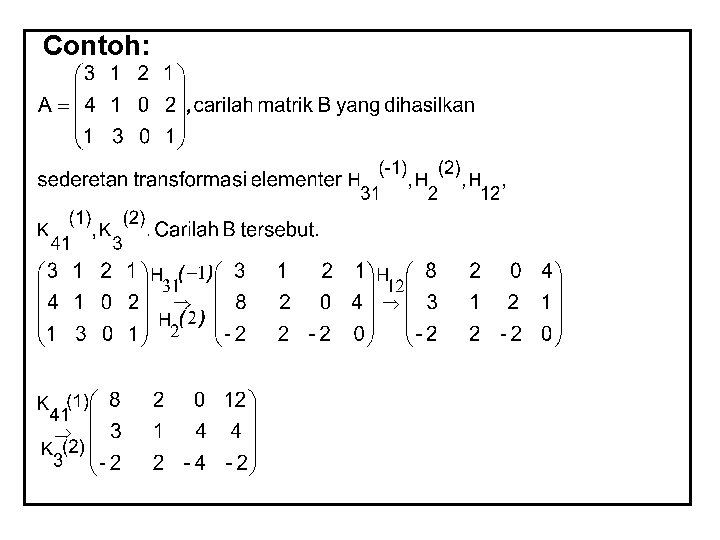
Transformasi (operasi) Elementer pada Baris dan Kolom Matriks Transformasi Elamenter pada matriks adalah: Ø Penukaran tempat baris ke i dan ke j (baris ke i dijadikan baris ke j dijadikan baris ke i), ditulis Hij (A) Ø Penukaran tempat kolom ke i dan kolom ke j (kolom ke i dijadikan kolom ke j atau sebaliknya), ditulis K ij (A) Ø Memperkalikan baris ke i dengan skalar ≠ 0, ditulis H i (A) Ø Memperkalikan kolom ke i dengan ≠ 0, ditulis K i (A) Ø Menambah baris ke i dengan kali baris ke j, ditulis H (A) ij

Ø Menambah kolom ke i dengan kali kolom ke j, ditulis K ij (A) Kadang untuk operasi (1) dan (3) dapat dilakukan dalam satu langkah : Menambah 1 kali baris ke i dengan 2 kali baris ke j, ditulis H i j (A) Demikian pula untuk operasi (2) dan (4) Bila menggunakan operasi baris maka disebut operasi baris elementer (OBE)

Contoh:

Invers Suatu Transformasi Linier Jika suatu transformasi elementer adalah: • A = H -1(B) = Hij (B) ij • A = K ij -1(B) = K ij (B) • A=H -1 1/ (B) = H i (B) i • A=K i -1 1/ (B) = K i (B) • A =H -1 (B) = H ij ij (B) A = K ij -1 (B) = K ij (B)

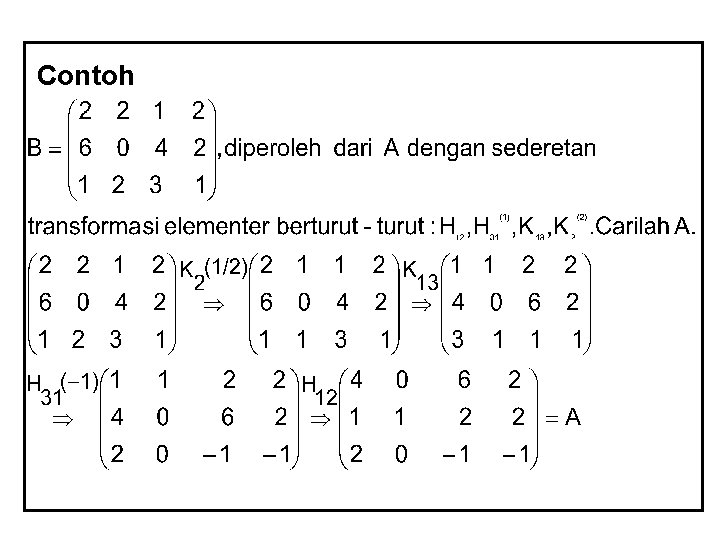
Contoh

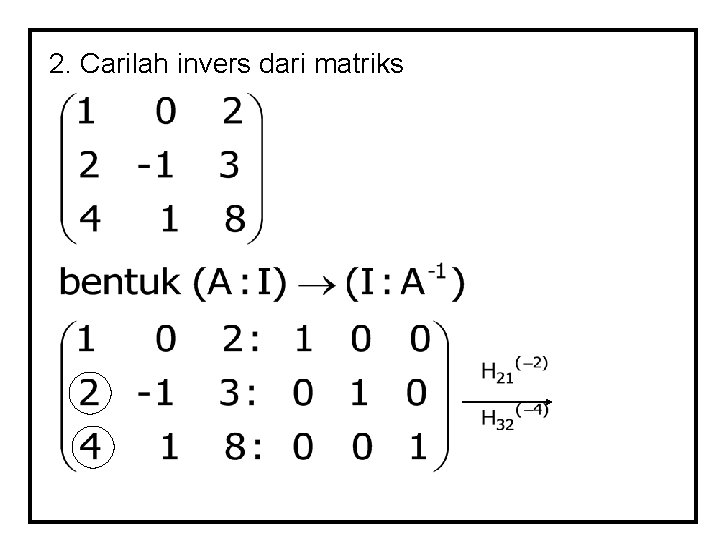
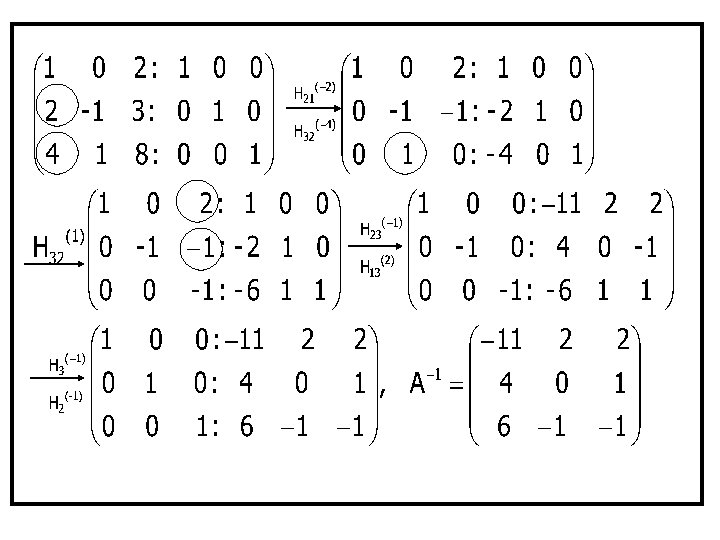
Penggunaan OBE • Mencari Rank Matriks Adalah jumlah maksimum baris/kolom yang bebas linier ( tidak semua unsur dalam suatu baris/kolom nol) • Mecari invers matriks OBE ( A: I ) -1 ( I: A )

Contoh Maka rank matriks A = 2

2. Carilah invers dari matriks