Matrices Inverses and Systems of equations KUS objectives

Matrices: Inverses and Systems of equations KUS objectives BAT solve systems of equations using inverse matrices – modelling with matrices

Write as a matrix multiplication Find the inverse matrix (using calc) Multiply through by the inverse

WB 12 Tyler invested a total of £ 5000 across three different accounts; a savings account; a property bond a share dealing account Tyler invested £ 400 more in the property bond account than in the saving account After one year • The savings account increased in value by 1. 5% • The property bond account had increased in value by 3. 5% • The share dealing account had decreased in value by 2. 5% • The total value across Tylers three accounts had increased by £ 79 Form and solve a matrix equation to find out how much money was invested by Tyler in each account Total at start is 100 more males at start After 1 year

WB 12 (cont) Form and solve a matrix equation to find out how much money was invested by Tyler in each account Find the inverse matrix (using calc) Multiply through by the inverse So the solution is Check this works in the original question

WB 13 A colony of 1000 mole rats is made up of adult males, adult females and youngsters. Originally there were 100 more adult females than adult males After one year • The number of adult males had increased by 2% • The number of adult females had increased by 3% • The number of youngsters had decreased by 4% • The total number mole-rats had decreased by 20 Form and solve a matrix equation to find out how many of each type of molerat were in the original colony Total at start is 100 more males at start After 1 year

WB 13 (cont) Form and solve a matrix equation to find out how many of each type of mole-rat were in the original colony Find the inverse matrix (using calc) Multiply through by the inverse So the solution is Check this works in the original question

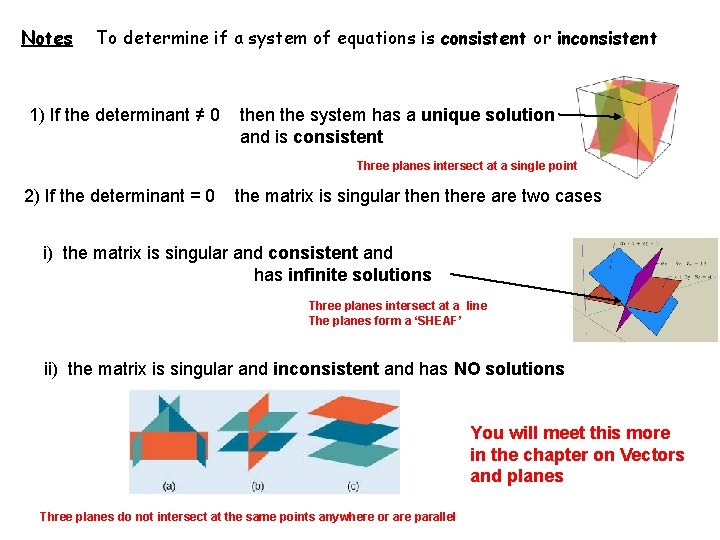
Notes To determine if a system of equations is consistent or inconsistent 1) If the determinant ≠ 0 then the system has a unique solution and is consistent Three planes intersect at a single point 2) If the determinant = 0 the matrix is singular then there are two cases i) the matrix is singular and consistent and has infinite solutions Three planes intersect at a line The planes form a ‘SHEAF’ ii) the matrix is singular and inconsistent and has NO solutions You will meet this more in the chapter on Vectors and planes Three planes do not intersect at the same points anywhere or are parallel

WB 15 a For each of the following values of k, determine whether the system of equations below is consistent or inconsistent. If consistent, determine whethere is a unique solution or an infinity of solutions. In each case, identify the geometric configuration of the planes corresponding to each value of k a) k = 0 b) k = 1 c) k = -6 1) If the determinant ≠ 0 then the system has a unique solution and is consistent Three planes intersect at a single point

WB 15 b For each of the following values of k, determine whether the system of equations below is consistent or inconsistent. If consistent, determine whethere is a unique solution or an infinity of solutions. In each case, identify the geometric configuration of the planes corresponding to each value of k a) k = 0 b) k = 1 c) k = -6 2) If the determinant = 0 the matrix is singular then there are two cases You need to determine if the system is consistent: Eliminate one of the variables from the set of equations. If the resulting two equations are consistent then the system is consistent: equations (4) and (5) are consistent because one is a linear multiple of the other. Any values of x and y that satisfy (4) also satisfy (5)

WB 15 b For each of the following values of k, determine whether the system of equations below is consistent or inconsistent. If consistent, determine whethere is a unique solution or an infinity of solutions. In each case, identify the geometric configuration of the planes corresponding to each value of k a) k = 0 b) k = 1 c) k = -6 2) If the determinant = 0 the matrix is singular then there are two cases You need to determine if the system is consistent: Eliminate one of the variables from the set of equations. If the resulting two equations are consistent then the system is consistent the system is Inconsistent and has no solutions: equations (4) and (5) are inconsistent because they are not solvable. No values of y and z satisfy both simultaneously

KUS objectives BAT solve systems of equations using inverse matrices – modelling with matrices self-assess One thing learned is – One thing to improve is –

END