Matrices Introduction Matrices Introduction L O All students

Matrices Introduction

Matrices Introduction L. O. All students are confident with: - what a matrix is - the dimensions of matrices - special cases - operations on matrices

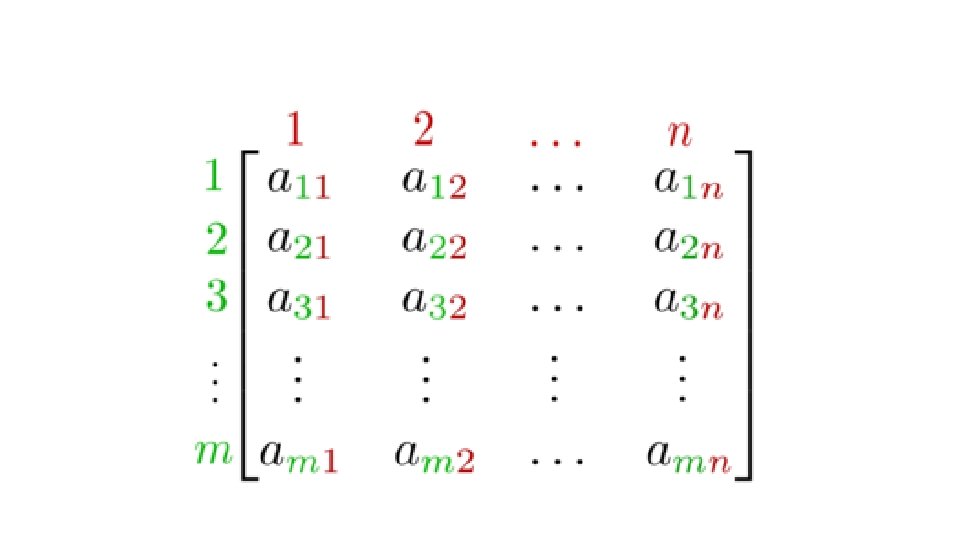
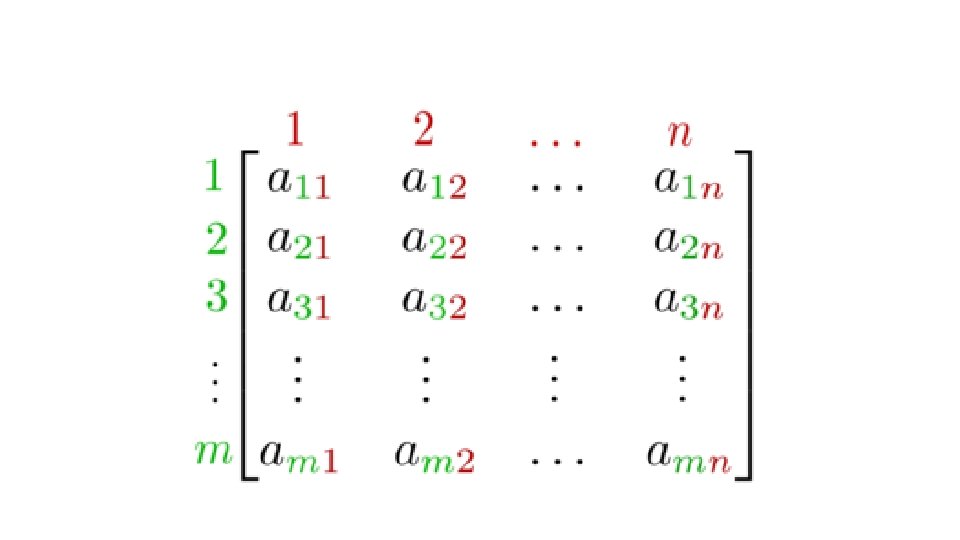
Columns Rows

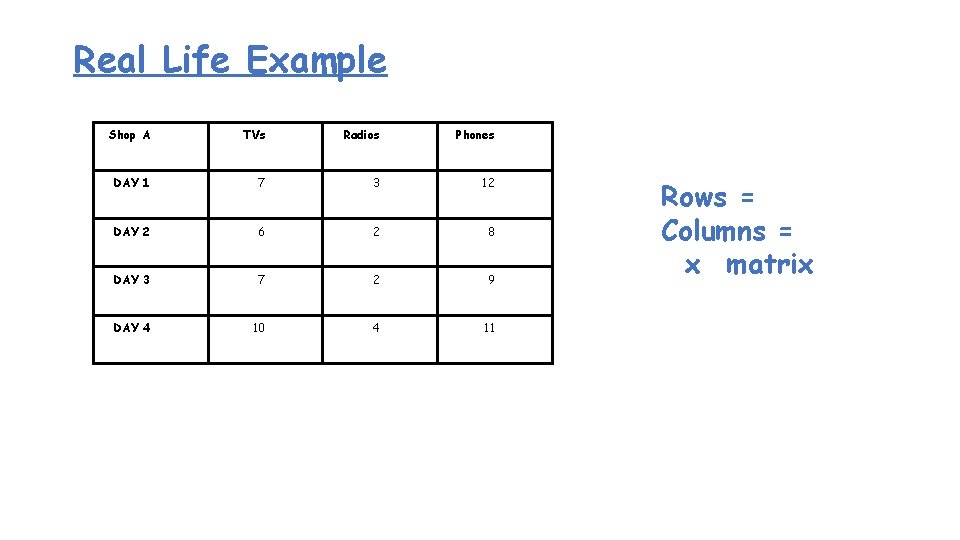
Real Life Example Shop A TVs Radios Phones DAY 1 7 3 12 DAY 2 6 2 8 DAY 3 7 2 9 DAY 4 10 4 11 Rows = Columns = x matrix

Write the dimensions of the following matrices b) d)

Write the dimensions of the following matrices b) b) 2 rows 1 row 2 columns 3 columns The matrix is 2 x 2 The matrix is 1 x 3 d) d) 2 rows 3 rows 1 column 2 columns

Note Special Cases: Vectors Row Vectors and Column Vectors Submatrix Zero Matrix Diagonal Matrix Triangular Matrix

Matrix Operations: Equal Matrices

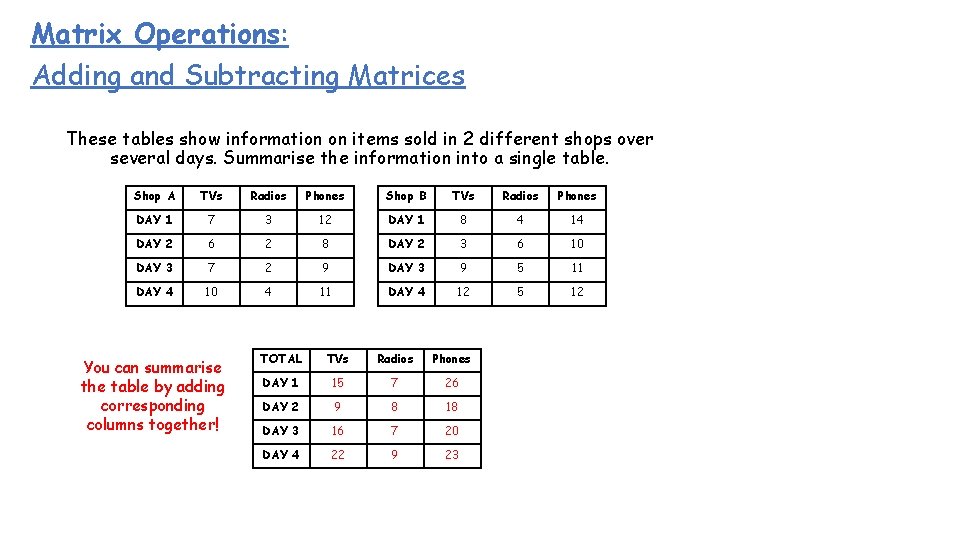
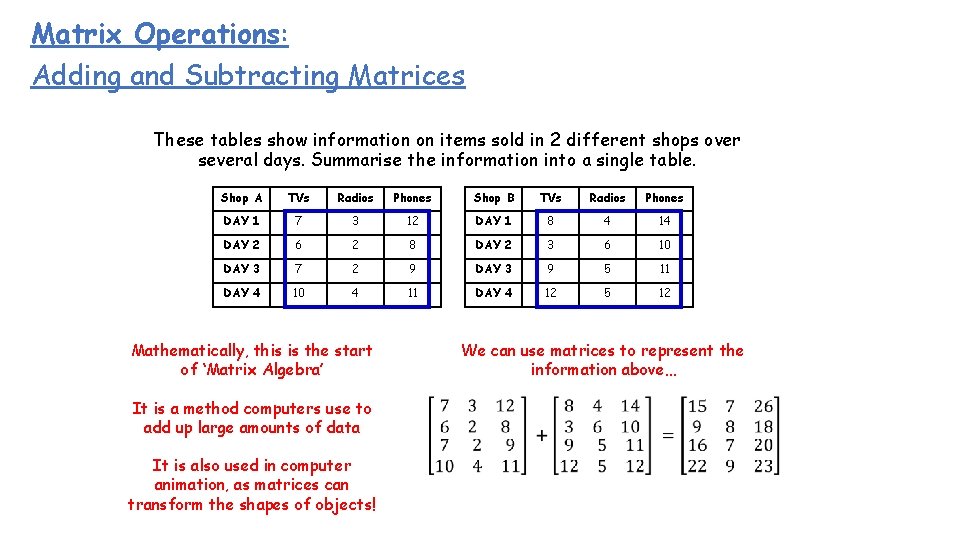
Matrix Operations: Adding and Subtracting Matrices These tables show information on items sold in 2 different shops over several days. Summarise the information into a single table. Shop A TVs Radios Phones Shop B TVs Radios Phones DAY 1 7 3 12 DAY 1 8 4 14 DAY 2 6 2 8 DAY 2 3 6 10 DAY 3 7 2 9 DAY 3 9 5 11 DAY 4 10 4 11 DAY 4 12 5 12 You can summarise the table by adding corresponding columns together! TOTAL TVs Radios Phones DAY 1 15 7 26 DAY 2 9 8 18 DAY 3 16 7 20 DAY 4 22 9 23

Matrix Operations: Adding and Subtracting Matrices These tables show information on items sold in 2 different shops over several days. Summarise the information into a single table. Shop A TVs Radios Phones Shop B TVs Radios Phones DAY 1 7 3 12 DAY 1 8 4 14 DAY 2 6 2 8 DAY 2 3 6 10 DAY 3 7 2 9 DAY 3 9 5 11 DAY 4 10 4 11 DAY 4 12 5 12 Mathematically, this is the start of ‘Matrix Algebra’ It is a method computers use to add up large amounts of data It is also used in computer animation, as matrices can transform the shapes of objects! We can use matrices to represent the information above…

Matrix Operations: Adding and Subtracting Matrices Practice To begin with, you need to know how to solve problems involving the addition and subtraction of matrices, and be able to state the ‘order’ of a matrix (its dimensions) You can add and subtract matrices only when they have the same dimensions Calculate A + B Calculate A - B

Matrix Operations: Adding and Subtracting Matrices Practice - Extension Calculate the values of x and y in the matrix equation below. 1) 1) 2) Multiply all by 3 2) Add 1) and 2) Divide by 5 You can then find y by substitution!

Matrix Operations: Multiplying a Matrix by a Scalar You need to be able to multiply a matrix by a number… Calculate: a) 2 A b)-3 A

Matrix Operations: Multiplying a Matrix by a Scalar You need to be able to multiply a matrix by a number… Calculate: a) 2 A a) Just multiply each part by 2 b) Just multiply each part by -3 b)-3 A So to multiply a matrix by a number, you just multiply each part in the matrix separately

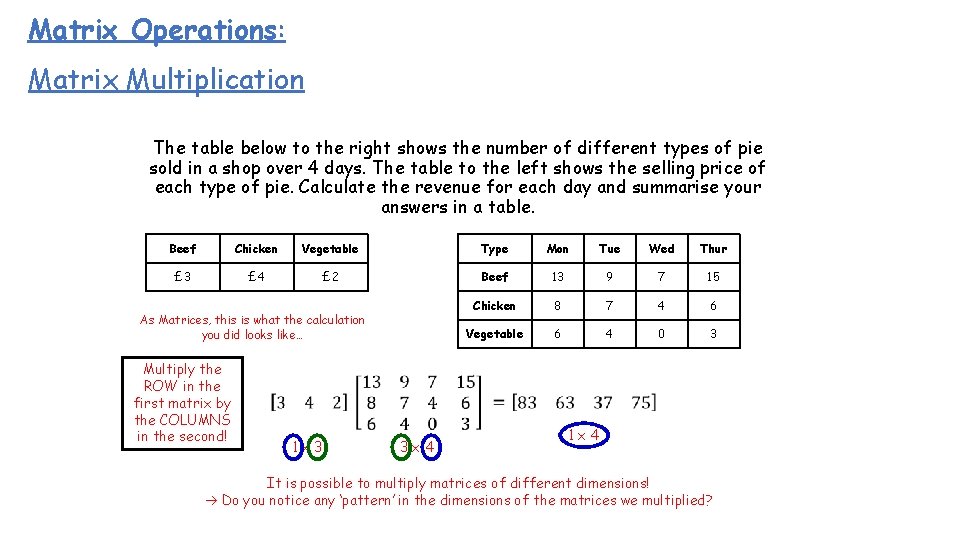
Matrix Operations: Matrix Multiplication The table below to the right shows the number of different types of pie sold in a shop over 4 days. The table to the left shows the selling price of each type of pie. Calculate the revenue for each day and summarise your answers in a table. Beef Chicken Vegetable Type Mon Tue Wed Thur £ 3 £ 4 £ 2 Beef 13 9 7 15 Chicken 8 7 4 6 Vegetable 6 4 0 3 As Matrices, this is what the calculation you did looks like… Multiply the ROW in the first matrix by the COLUMNS in the second! 1 x 3 3 x 4 1 x 4 It is possible to multiply matrices of different dimensions! Do you notice any ‘pattern’ in the dimensions of the matrices we multiplied?

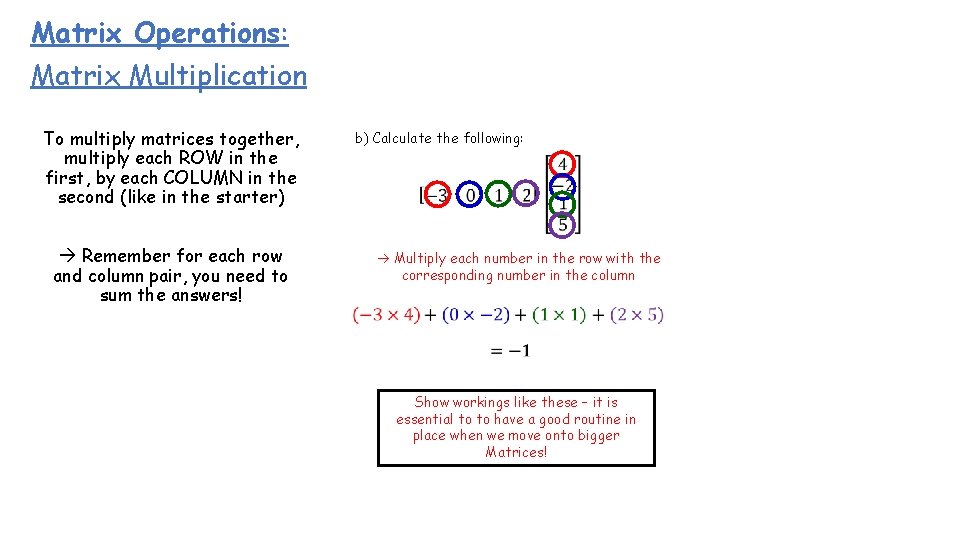
Matrix Operations: Matrix Multiplication To multiply matrices together, multiply each ROW in the first, by each COLUMN in the second (like in the starter) Remember for each row and column pair, you need to sum the answers! a) Calculate the following Multiply each number in the row with the corresponding number in the column

Matrix Operations: Matrix Multiplication To multiply matrices together, multiply each ROW in the first, by each COLUMN in the second (like in the starter) Remember for each row and column pair, you need to sum the answers! b) Calculate the following: Multiply each number in the row with the corresponding number in the column Show workings like these – it is essential to to have a good routine in place when we move onto bigger Matrices!

Matrix Operations: Matrix Multiplication The values of x and y in these pairs of Matrices are the same. Calculate what x and y must be! As an equation Multiply by 2 Multiply by 5 Add the two equations together Divide by 16 Then find x