Matrices conceptos generales Objetivos Comprender conceptualmente la matriz

Matrices: conceptos generales Objetivos: • Comprender conceptualmente la matriz y la notación matricial. • Identificar los diferentes tipos de matrices. Introducción: En este curso iniciamos abordando el álgebra lineal que es una disciplina matemática en la que estudia los espacios vectoriales y las transformaciones lineales. Tiempo aproximado de estudio: 30 minutos.

Columnas Matriz Es un arreglo rectangular de a elementos arreglados en m filas y n columnas. A= En el siguiente gráfico se muestra la forma general de la matriz. Filas a 11 a 12 … a 1 n a 21 a 22 … a 2 n. . . am 1 am 2 … amn Está matriz esta constituida por elementos amn y tiene un tamaño m x n.

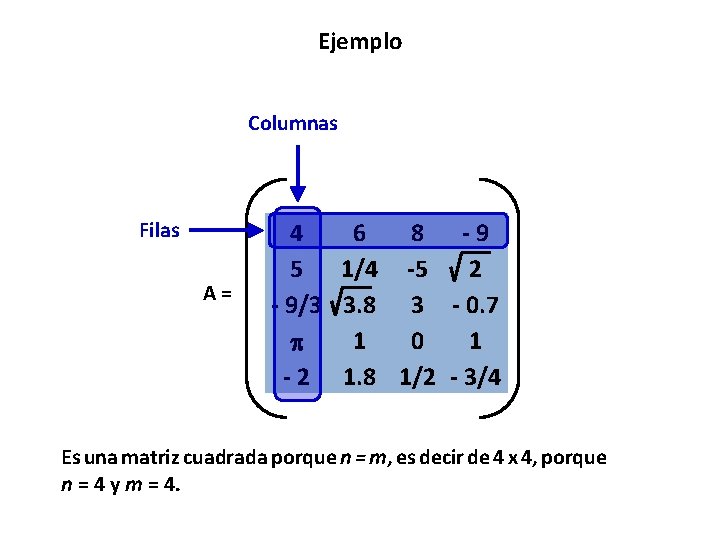
Ejemplo Columnas Filas A= 4 6 8 -9 5 1/4 -5 2 - 9/3 3. 8 3 - 0. 7 1 0 1 - 2 1. 8 1/2 - 3/4 Es una matriz cuadrada porque n = m, es decir de 4 x 4, porque n = 4 y m = 4.

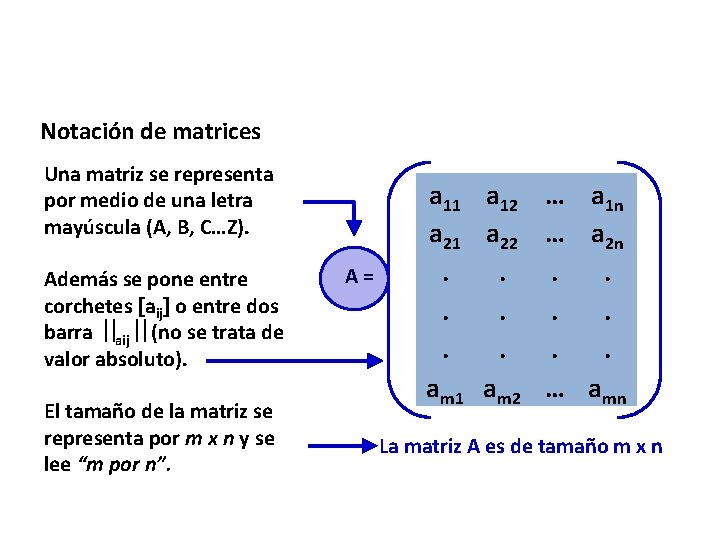
Notación de matrices Una matriz se representa por medio de una letra mayúscula (A, B, C…Z). Además se pone entre corchetes aij o entre dos barra aij (no se trata de valor absoluto). El tamaño de la matriz se representa por m x n y se lee “m por n”. A= a 11 a 12 … a 1 n a 21 a 22 … a 2 n. . . am 1 am 2 … amn La matriz A es de tamaño m x n

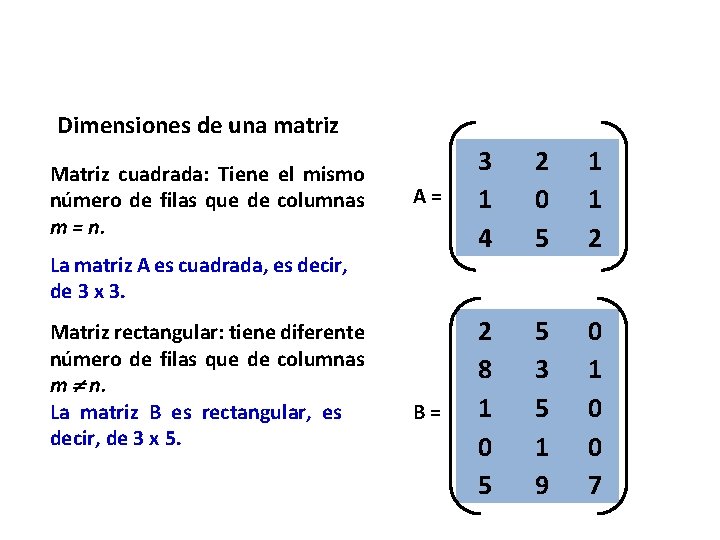
Dimensiones de una matriz Matriz cuadrada: Tiene el mismo número de filas que de columnas m = n. A= 3 1 4 2 0 5 1 1 2 B= 2 8 1 0 5 5 3 5 1 9 0 1 0 0 7 La matriz A es cuadrada, es decir, de 3 x 3. Matriz rectangular: tiene diferente número de filas que de columnas m n. La matriz B es rectangular, es decir, de 3 x 5.

Matriz escalar : es una matriz cuadrada formada por 1 elemento. Tiene solamente 1 fila y 1 columna. Se denota por = a 11 1 x 1 El elemento a 11 es un número real y la dimensión o tamaño de la matriz es de 1 x 1. Se le denomina escalar. = 3

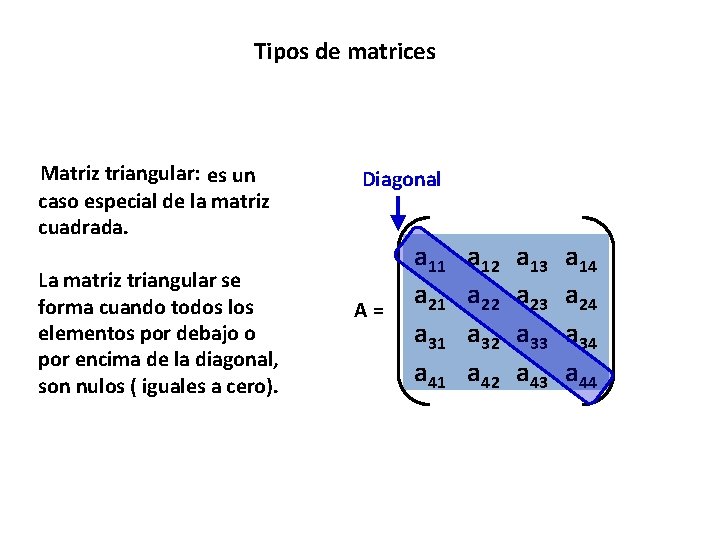
Tipos de matrices Matriz triangular: es un caso especial de la matriz cuadrada. La matriz triangular se forma cuando todos los elementos por debajo o por encima de la diagonal, son nulos ( iguales a cero). Diagonal A= a 11 a 21 a 31 a 41 a 12 a 22 a 32 a 42 a 13 a 23 a 33 a 43 a 14 a 24 a 34 a 44

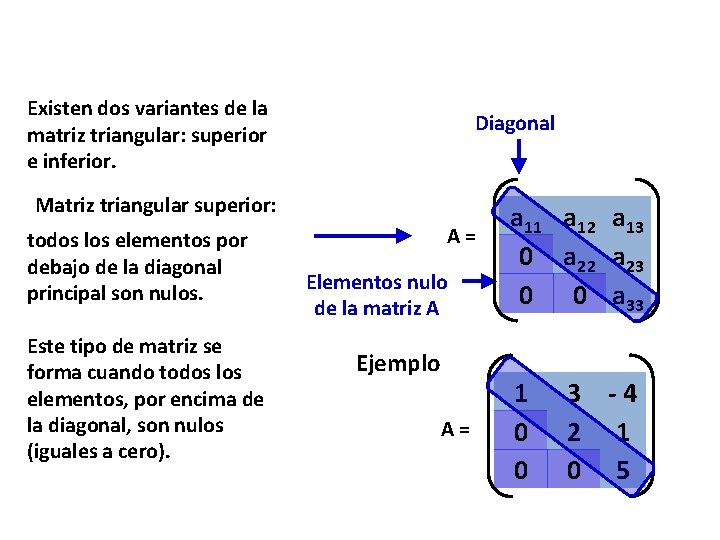
Existen dos variantes de la matriz triangular: superior e inferior. Diagonal Matriz triangular superior: todos los elementos por debajo de la diagonal principal son nulos. Este tipo de matriz se forma cuando todos los elementos, por encima de la diagonal, son nulos (iguales a cero). A= Elementos nulo de la matriz A Ejemplo A= a 11 a 12 a 13 0 a 22 a 23 0 0 a 33 1 0 0 3 -4 2 1 0 5

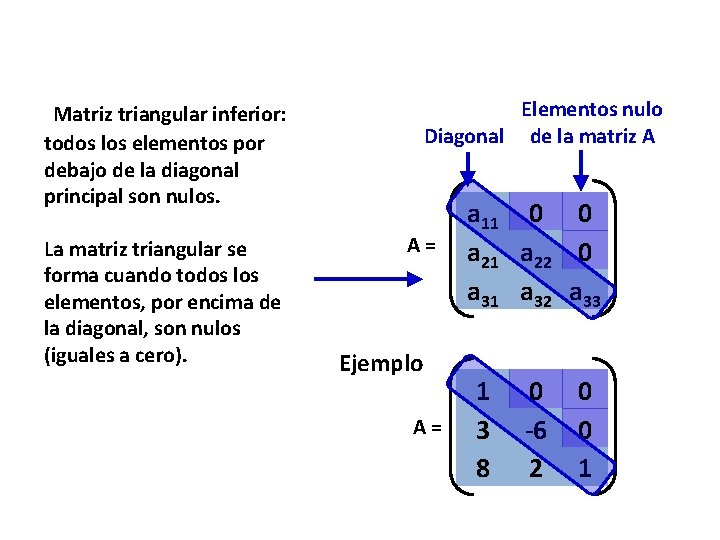
Elementos nulo Diagonal de la matriz A Matriz triangular inferior: todos los elementos por debajo de la diagonal principal son nulos. La matriz triangular se forma cuando todos los elementos, por encima de la diagonal, son nulos (iguales a cero). A= Ejemplo A= a 11 0 0 a 21 a 22 0 a 31 a 32 a 33 1 3 8 0 -6 2 0 0 1

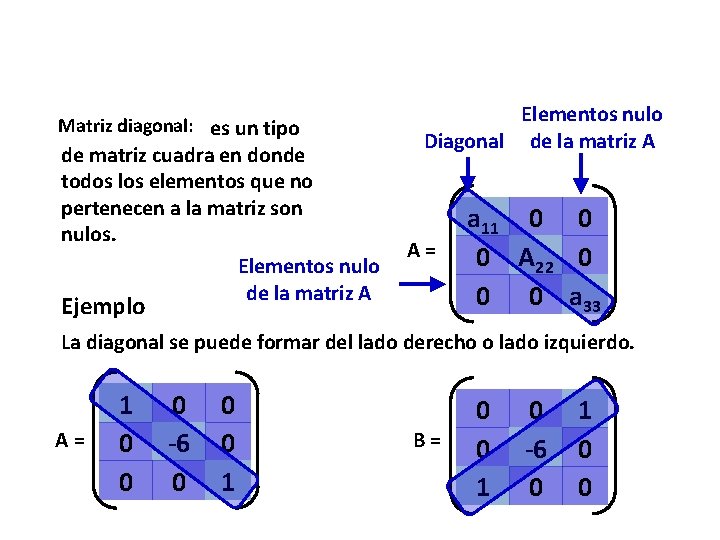
Matriz diagonal: es un tipo de matriz cuadra en donde todos los elementos que no pertenecen a la matriz son nulos. Elementos nulo de la matriz A Elementos nulo Diagonal de la matriz A A= Ejemplo a 11 0 0 0 A 22 0 0 0 a 33 La diagonal se puede formar del lado derecho o lado izquierdo. A= 1 0 0 0 -6 0 0 0 1 B= 0 0 1 0 -6 0 1 0 0

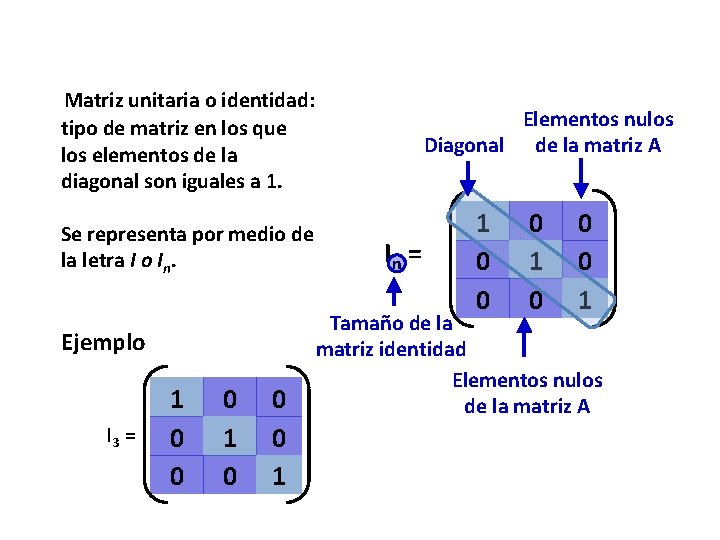
Matriz unitaria o identidad: tipo de matriz en los que los elementos de la diagonal son iguales a 1. Se representa por medio de la letra I o In. Ejemplo I 3 = 1 0 0 0 1 Elementos nulos Diagonal de la matriz A In = 1 0 0 0 1 Tamaño de la matriz identidad Elementos nulos de la matriz A

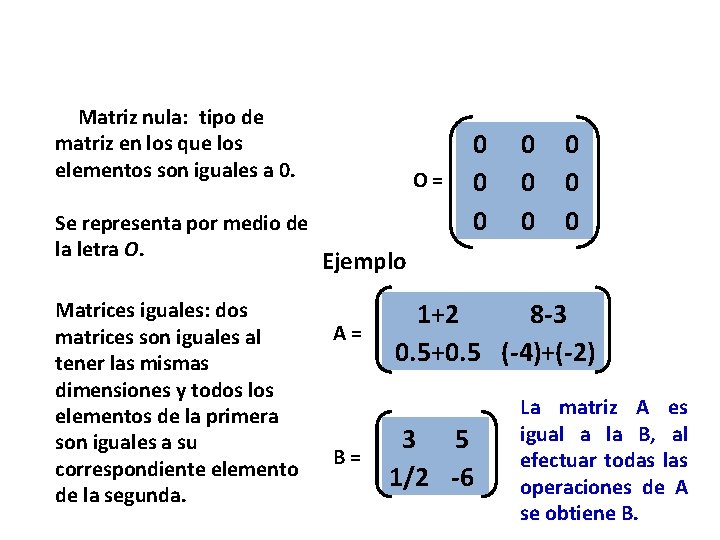
Matriz nula: tipo de matriz en los que los elementos son iguales a 0. Se representa por medio de la letra O. Matrices iguales: dos matrices son iguales al tener las mismas dimensiones y todos los elementos de la primera son iguales a su correspondiente elemento de la segunda. O= 0 0 0 0 0 Ejemplo A= B= 1+2 8 -3 0. 5+0. 5 (-4)+(-2) 3 5 1/2 -6 La matriz A es igual a la B, al efectuar todas las operaciones de A se obtiene B.

Referencias bibliográficas Unidad 1 Matrices y Determinantes. (pp. 17 a 27) disponible en. http: //gc. scalahed. com/buscador/recurso/ver/13166