MATRICES AND VECTORS FOR COMPUTER GRAPHICS PART 1

MATRICES AND VECTORS FOR COMPUTER GRAPHICS PART 1

Cartesian Coordinates I’m assuming everyone knows what this is: (1, 2) (0, 0)

Vectors and Points A vector is a direction A point is a fixed position v= [x, y, ] T p = (a, b) p v

Vector Addition We can add vectors to vectors = new vector V 1+v 2 = [x 1+x 2, y 1+y 2]T v 2 v 1+v 2 v 1 v 2

Vector Addition Add a vector to a point to obtain a new point. p=[1, 1]T p’ v = [2, 2]T p’ = ? v What is happening here? p

Confusing Points and Vectors Consider the point and the vector P = P 0 + b 1 v 1+ b 2 v 2 +…. +bnvn v=a 1 v 1+ a 2 v 2 +…. +anvn They appear to have the similar representations p=[b 1 b 2 b 3] v=[a 1 a 2 a 3] v which confuses the point with the vector v A vector has no position p Vectors can be placed anywhere point: fixed Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 6

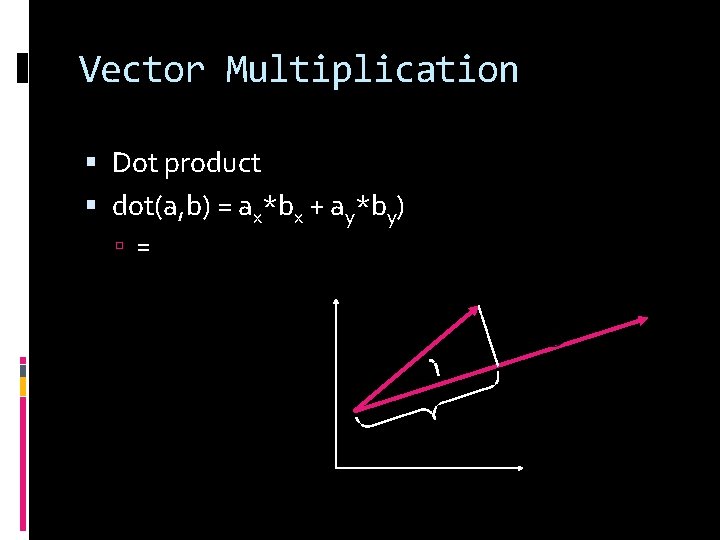
Vector Multiplication Dot product dot(a, b) = ax*bx + ay*by) =

Scalar Multiplication v*s = [vx*s, vy*s] T v v*s

Vector Length How to make a vector unit length (normalize) ?

Coordinate Systems Consider a basis v 1, v 2, …. , vn e. g. 3 d space with 3 vectors pointing in the directions of each axis A vector is written v=a 1 v 1+ a 2 v 2 +…. +anvn The list of scalars {a 1, a 2, …. an}is the representation of v with respect to the given basis We can write the representation as a row or column array of scalars a=[ a 1 a 2 …. an]T= Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 10

In 3 D v=a 1 v 1+ a 2 v 2 + a 3 v 3 v 2 v v 3 v 1

Example v=2 v 1+3 v 2 -4 v 3 a=[2 3 – 4]T Note that this representation is with respect to a particular basis For example, in Open. GL we start by representing vectors using the object basis but later the system needs a representation in terms of the camera or eye basis Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 12

Coordinate Systems Which is correct? v v Both are because vectors have no fixed location Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 13

Frames A coordinate system is insufficient to represent points We can add a single point, the origin, to the basis vectors to form a frame v 2 v 1 P 0 v 3 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 14

Representation in a Frame determined by (P 0, v 1, v 2, v 3) Within this frame, every vector can be written as v=a 1 v 1+ a 2 v 2 +…. +anvn Every point can be written as P = P 0 + b 1 v 1+ b 2 v 2 +…. +bnvn Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 15

What is a matrix? Theorem 1: A matrix has nothing to do with Keanu Reeves (probably) m x n array of scalars M=

A Frame in Matrix Form Where P 0 is the origin of the frame M: v 2 P 0 v 3 v 1

Matrix Operations Scalar multiplication, addition, matrix-matrix multiplication… In this class, we really only care about: matrix-matrix multiplications with square (m x m) matrices matrix-point multiplication

Matrix-Point Multiplication

Matrix-Matrix Multiplication Does A*B = B*A? What does the identity do?

Example

Properties of Matrices Associative A(BC) = (AB)C NOT commutative (usually) AB = BA However, IA = AI = A

What are matrices used for in CG? Transformations: Rotation, Translation, Scale, Shear