Matric teorija 2013 09 04 Matric teorija Matricos
















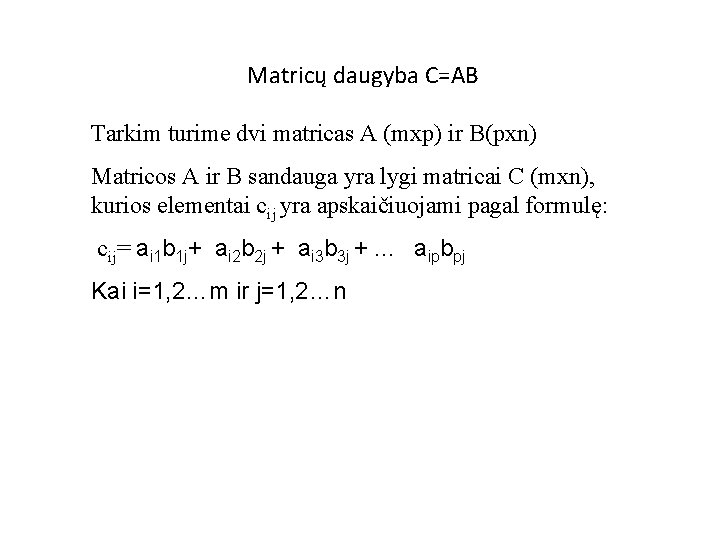


























- Slides: 46

Matricų teorija 2013 -09 -04

Matricų teorija • Matricos ir vektoriaus sąvokos • Veiksmai su matricomis • Dauginės regresijos įverčių skaičiavimas pasitelkiant matricas

mxn matavimų stačiakampe matrica, vadiname aibę skaičių, sudėliotų stačiakampe forma, turinčia m eilučių ir n stulpelių a 11 A= a 21. . . am 1 a 12 a 13. . . a 1 n a 22 a 23. . . a 2 n … … am 2 am 3. . . amn 1 xn matavimų matrica vadinama vektoriumi- eilute mx 1 matavimų matrica vadinama vektoriumi- stulpeliu Vektorius žymime mažąja raide pvz. a

Matricų rūšys • • Nulinė Kvadratinė Diagonalinė Skaliarinė Vienetinė Simetriška Sub-matrica

Vienetinė matrica Kvadratinę nxn matavimų matricą, kurios pagrindinės įstrižainės elementai yra lygūs 1, o visi likę elementai yra lygūs 0 vadiname vienetine matrica ir žymine raide I 1 I= 0. . . 0 0 1 0 0 0. . . 0 . . . 1

Veiksmai su matricomis • • • Sudėtis Atimtis Daugyba Dalyba Diferencijavimas

Matricų suma mxn matavimų dviejų matricų A ir B suma A+B yra lygi mxn matavimų matricai C, kurios elementai cij yra lygūs A ir B matricų atitinkamų elementų sumai aij + bij. a 11 a 12 a 13. . . a 1 n A= a 21 a 22 a 23… a 2 n. . . am 1 am 2 am 3. . . amn b 11 b 12 b 13. . . b 1 n B= b 21 b 22 b 23 … b 2 n. . . bm 1 bm 2 bm 3. . . bmn

mxn C=A+B, kur kiekvienam i, j cij = aij + bij. c 11 c 12 c 13 C= c 21 c 22 c 23 cm 1 cm 2 cm 3 c 1 n c 2 n cmn = a 11+b 11 a 12+b 12 a 13+b 13 … a 1 n+b 1 n a 21+b 21 a 22+b 22 a 23+b 23 … a 2 n+b 2 n am 1+bm 1 am 2+bm 2 am 3+bm 3 … amn+bmn

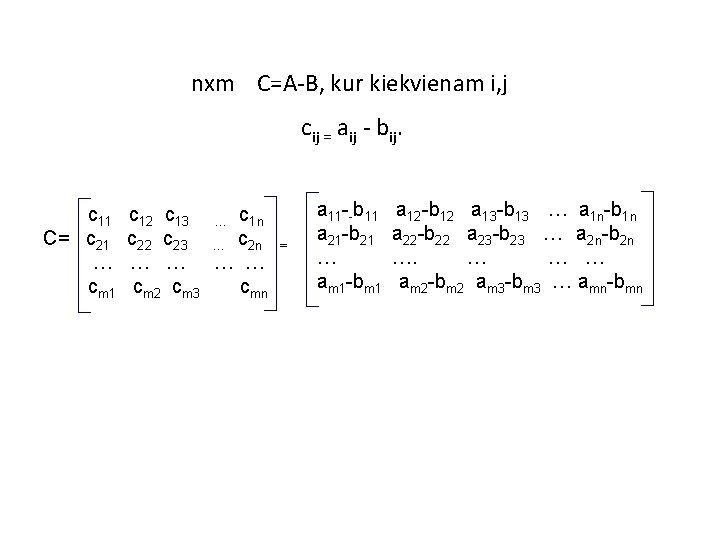
Matricų atimtis mxn matavimų dviejų matricų A ir B skirtumas A-B yra lygus mxn matavimų matricai C, kurios elementai cij yra lygūs A ir B matricų atitinkamų elementų skirtumui aij - bij. a 11 a 12 a 13. . . a 1 n A= a 21 a 22 a 23… a 2 n. . . am 1 am 2 am 3. . . amn b 11 b 12 b 13. . . b 1 n B= b 21 b 22 b 23 … b 2 n. . . bm 1 bm 2 bm 3. . . bmn

nxm C=A-B, kur kiekvienam i, j cij = aij - bij. c 11 C= c 21 … cm 1 c 12 c 13 … c 1 n c 22 c 23 … c 2 n … … cm 2 cm 3 cmn = a 11 --b 11 a 21 -b 21 … am 1 -bm 1 a 12 -b 12 a 13 -b 13 … a 1 n-b 1 n a 22 -b 22 a 23 -b 23 … a 2 n-b 2 n …. … … … am 2 -bm 2 am 3 -bm 3 … amn-bmn

Matricų daugyba • Matricos daugyba iš konstantos • Matricos daugyba iš vektoriaus • Matricos daugyba iš matricos

Matricos daugyba iš konstantos A=k. A mxn matavimų matricą padauginus iš bet kokio skaičiaus k, gauname naują mxn matavimų matricą k. A, kurios elementai yra lygūs matricos A atitinkamiems elementams, padaugintiems iš skaičiaus k. a 11 a 12 a 13. . . a 1 n A= a 21 a 22 a 23… a 2 n. . . am 1 am 2 am 3. . . amn ka 11 ka 12 ka 13. . . ka 1 n k. A= ka 21 ka 22 ka 23… ka 2 n. . . kam 1 kam 2 kam 3. . . kamn

Sąvokos: • Suderinamos matricos • Matricų transponavimas

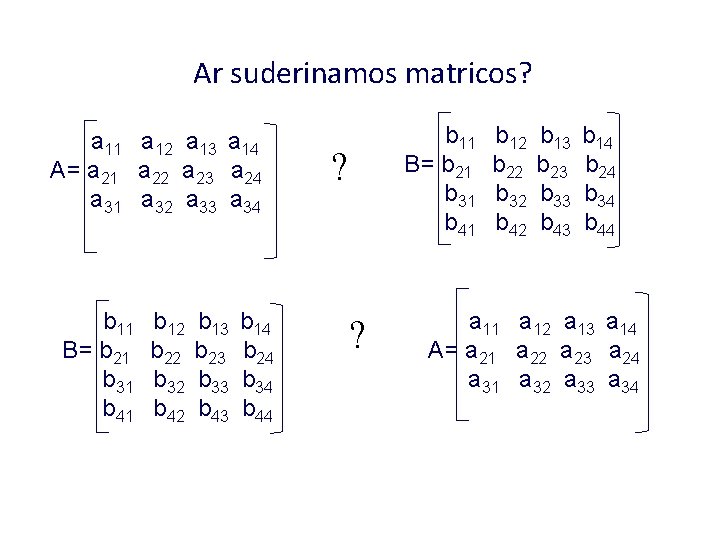
Suderinamos matricos Dauginti galima tik suderinamas matricas A ir B matricos yra suderinamos jeigu matricos A stulpelių skaičius yra lygus matricos B eilučių skaičiui a 11 a 12 a 13 a 14 A= a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 3 x 4 ? b 11 b 12 b 13 b 14 B= b 21 b 22 b 23 b 24 b 31 b 32 b 33 b 34 3 x 4

Ar suderinamos matricos? a 11 a 12 a 13 a 14 A= a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 b 11 B= b 21 b 31 b 41 b 12 b 22 b 32 b 42 b 13 b 23 b 33 b 43 b 14 b 24 b 34 b 44 b 11 B= b 21 b 31 b 41 ? ? b 12 b 22 b 32 b 42 b 13 b 23 b 33 b 43 b 14 b 24 b 34 b 44 a 11 a 12 a 13 a 14 A= a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34

Matricų transponavimas Matricą A (mxn) transponuojame sukeisdami stulpelius ir eilutes vietomis. Transponuota matrica žymima A’ a 11 a 12 a 13. . . a 1 n A= a 21 a 22 a 23… a 2 n. . . am 1 am 2 am 3. . . amn mxn a 11 a 21 a 31. . . am 1 A’= a 12 a 22 a 32… am 2. . . a 1 n a 2 n a 3 n. . . amn nxm

Matricų daugybos principas Tarkim turim matricą A (mxp) matavimų ir B (pxn) j- stulpelis i eilutė cij= ai 1 b 1 j+ ai 2 b 2 j + ai 3 b 3 j +. . . aipbpj

Dviejų vektorių daugyba Tarkim a yra vektorius- eilutė (1 xn) matavimų , o b vektorius - stulpelis (nx 1) Vektorių a ir b sandauga bus lygi skaičiui c, t. y. , a x b = c, kur skaičius c apskaičiuojamas pagal formulę: c= a 11 b 11+ a 12 b 21 + a 13 b 31 +. . . a 1 nbn 1 a = [a 11 a 12 a 13. . . a 1 n] b= b 11 b 21 b 31. . . bn 1 a x b= a 11 b 11+ a 12 b 21 + a 13 b 31 +. . . a 1 nbn 1=c
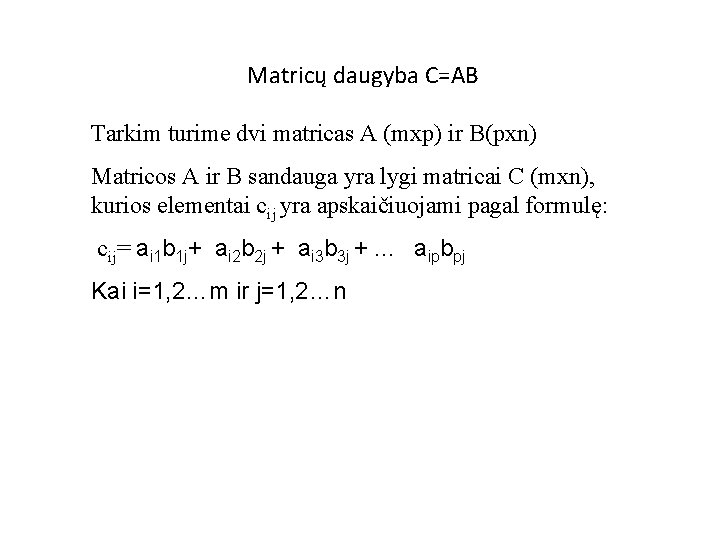
Matricų daugyba C=AB Tarkim turime dvi matricas A (mxp) ir B(pxn) Matricos A ir B sandauga yra lygi matricai C (mxn), kurios elementai cij yra apskaičiuojami pagal formulę: cij= ai 1 b 1 j+ ai 2 b 2 j + ai 3 b 3 j +. . . aipbpj Kai i=1, 2…m ir j=1, 2…n

Matricų sandaugos savybės • • • Dauginti galima tik suderinamas matricas AB BA A(BC)=(AB)C A(B+C)=AB+AC (A+B)C=AC+BC IA=AI=A

Determinanto sąvoka Tik kvadratinės matricos! Kvadratinės matricos determinantas - tai skaičius, kuris yra lygus visų galimų elementų, priklausančių skirtingoms eilutėms ir stulpeliams sandaugų, padaugintų iš (-1)f , sumai a 11 a 12 a 13. . . a 1 n IAI= a 21 a 22 a 23… a 2 n. . . an 1 an 2 an 3. . . ann f- inversijų skaičius

Determinanto sąvoka |A| Perstatiniu vadinama skaičių kombinacija J=[j 1, j 2 j 3. . . jn], sudaryta iš dauginamų matricos elementų stulpelių numerių ir žymima J. Inversija vadinama perstatinio dviejų skaičių pora, kurioje pirmasis skaičius yra didesnis už antrąjį. f- inversijų skaičius

Matricos determinantas Tik kvadratinės matricos!!! Antros eilės matricos determinantu vadinsime tokį skaičių: a 11 a 12 [A]= a 21 a 22 = a 11 a 22 – a 12 a 21 Pvz. : 1 2 3 4 = 4 – 6 = -2

Trečios eilės matricos determinantu vadinsime tokį skaičių : a 11 a 12 a 13 [A]= a 21 a 22 a 23 a 31 a 32 a 33 [A] = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 – (a 13 a 22 a 31 + a 21 a 12 a 33 + a 11 a 23 a 32) Pvz. : 2 3 4 0 5 6 = 2× 5× 1+3× 6× 7+4× 0× 8–(4× 5× 7 + 0× 3× 1 + 2× 6× 8) =-100 7 8 1

N – tos eilės matricos determinanto apskaičiavimas Determinanto skleidimas eilute a 11 a 12. . . a 1 n a 21 a 22. . . a 2 n. . … ai 1 ai 2. . . ain. . … an 1 an 2. . . ann = ai 1 Ai 1+ ai 2 Ai 2+. . . + ain. A in Aij – matricos A elemento aij adjunktas. Aij= (-1)i+j Mij - minoras –

N – tos eilės matricos determinanto apskaičiavimas Determinanto skleidimas stulpeliu a 11 a 12. . . a 1 n a 21 a 22. . . a 2 n. . … ai 1 ai 2. . . ain. . … =a 1 j. A 1 j+ a 2 j. A 2 j+. . . + anj. Anj an 1 an 2. . . ann Aij – matricos A elemento aij adjunktas. Aij= (-1)i+j Mij - minoras –

Adjunkto ir minoro sąvokos Minoro sąvoka Pasirenkame A matricoje aij elementą. Išbraukiame i- eilutę ir j- stulpelį. Lieka n -1 matavimų matrica, kurios determinantas yra vadinamas elemento aij minoru ir žymime raide Mij Adjunkto sąvoka aij elemento adjunktas žymimas Aij ir yra lygus Aij=(-1)i+j Mij

Pvz. : Det. skaičiavimas skleidžiant stulpeliu 2 3 4 0 6 2 4 0 5 6 = - 3 A 12 + 5 A 22 - 8 A 32 = -3 7 1 + 5 7 1 - 8 0 6 = 7 8 1 =-3(0× 1 -6× 7) + 5 (2× 1 -7× 4) – 8 (2× 6 – 4× 0)= 126 – 130 – 96 = -100

Determinantų savybės 1. Jei matricos kurios nors eilutės arba stulpelio visi elementai yra lygūs 0, tai ir determinantas yra lygus 0 2. Jeigu dvi matricos eilutes sukeičiame vietomis, tai jų determinantų absoliučios reikšmės yra tos pačios, skiriasi tik ženklas

Determinantų savybės 3. Jeigu visi matricos A kurios nors eilutės elementai turi bendrą daugiklį, tai jį galima iškelti už determinanto ženklo, t. y D’=k. D a 11 a 12 a 13. . . a 1 n D= a 21 a 22 a 23… a 2 n. . . an 1 an 2 an 3. . . ann a 11 a 12 a 13. . . a 1 n D’= ka 21 ka 22 ka 23… ka 2 n. . . an 1 an 2 an 3. . . ann

Determinantų savybės 4. Matricos, kurios dvi eilutės yra vienodos, determinantas yra lygus 0 5. Matricos determinantas nepasikeis, jeigu prie vienos eilutės pridėsime kitą eilutę, padaugintą iš bet kokio skaičiaus nelygaus 0

Atvirkštinė matrica Skaičiai Matricos

Atvirkštinė matrica Tik kvadratinės matricos! Kvadratinės n matavimų matricos A atvirkštine matrica vadiname tokią kvadratinę n matavimų matricą A-1, kurios sandauga su A matrica yra lygi vienetinei n matavimų matricai E AA-1=A-1 A=I

Atvirkštinė matrica A 11 A 21 A 31. . . An 1 A-1 = 1/|A| A 12 A 22 A 32… An 2. . . A 1 n A 2 n A 3 n. . . Ann |A| - matricos A determinantas Aij- matricos elemento- aij- adjunktas

Lygčių sistemos sprendimas taikant matricų veiksmus a 11 x 1 + a 12 x 2 + a 13 x 3 =b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 =b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 =b 3 AX=B X=A-1 B

Matricos rangas r(A) a 11 a 12 a 13. . . a 1 n A= a 21 a 22 a 23… a 2 n. . . am 1 am 2 am 3. . . amn A(mxn) matricos rangas r(A) – tai maksimalus tiesiškai nepriklausomų A matricos stulpelių ir eilučių skaičius Matricos A rangas r(A) yra nustatomas, randant didžiausios kvadratinės submatricos, kurios determinantas nelygus nuliui, matavimų eilę

Matricos rangas r(A) Jeigu A(mxn) matricos rangas r(A) =k , tai, • visi k+1 eilės minorai yra lygūs nuliui • bent vienas k eilės minoras nėra lygus nuliui Jeigu turime dvi matricas A(mxn) ir B(nxk), tai sandaugos AB matricos rangas neviršija mažesnį rangą turinčios matricos rango Lygčių sistema Ax=b turės sprendinį, tik tuo atveju, jeigu matricos A(nxn) rangas r(A) yra lygus n

Matricų diferencijavimas a= a 1 a 2 a 31. . . an x= x 1 x 2 x 3. . . xn a’x= a 1 x 1+ a 2 x 2 + a 3 x 3 +. . . anxn

Matricų diferencijavimas a 11 a 21 a 31. . . an 1 a 12 a 22 a 32… an 2 x’A’x= [x 1, x 2, x 3, . . . xn]. . . a 1 n a 2 n a 3 n. . . ann x’A’x= x 1 x 2 x 3. . . xn a 11 x 12 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 +. . . +2 a 1 n x 1 xn + a 22 x 22 + 2 a 23 x 2 x 3 +. . . +2 a 2 n x 2 xn + a 33 x 32 +. . . +2 a 3 n x 2 xn. . . + ann xn 2

Matricų diferencijavimas . . .

Dauginės regresijos įverčių skaičiavimas pasitelkiant matricas • Įverčių skaičiavimas

Įverčių skaičiavimas • Duomenis pateikiame vektorių ir matricų forma Y= Y 1 Y 2 X= Y 3. . . Yn 1 X 12 X 13. . . X 1 m 1 X 22 X 23… X 2 m. . . 1 Xn 2 Xn 3. . . Xnm Y=Xβ+u β 1 β= β 2 β 3. . . βm u 1 u 2 u= u 3. . . un

Įverčių skaičiavimas MKM

Įverčių skaičiavimas MKM

Įverčių skaičiavimas MKM x, y –duomenys pateikti nuokrypiais nuo vidurkio

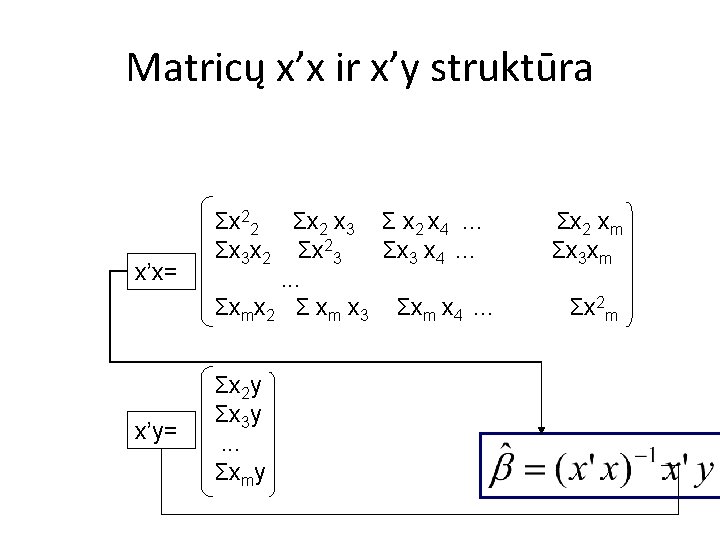
Matricų x’x ir x’y struktūra x’x= x’y= Σx 22 Σx 2 x 3 Σ x 2 x 4. . . Σx 3 x 2 Σx 23 Σx 3 x 4 …. . . Σxmx 2 Σ xm x 3 Σxm x 4 … Σx 2 y Σx 3 y. . . Σxmy Σx 2 xm Σx 3 xm Σx 2 m
 Atvirkstine matrica
Atvirkstine matrica Matricos adjunktas
Matricos adjunktas Matric multiplication
Matric multiplication Mátric
Mátric E sign ssp
E sign ssp John 13:35 message
John 13:35 message Mátric
Mátric Teorija sudara
Teorija sudara Rāmēšanas teorija
Rāmēšanas teorija Pijazeova teorija
Pijazeova teorija Agencijska teorija
Agencijska teorija Par nepar igra
Par nepar igra Teorija postavljanja ciljeva
Teorija postavljanja ciljeva Kvantitativna teorija novca
Kvantitativna teorija novca Adlerova teorija licnosti
Adlerova teorija licnosti Teorija i politika bilansa
Teorija i politika bilansa Bolbijeva teorija
Bolbijeva teorija Marina magdalena
Marina magdalena Teorija evolucije
Teorija evolucije Teorija sistema fon
Teorija sistema fon 4 osnovne emocije
4 osnovne emocije Sta je stepen u muzici
Sta je stepen u muzici Freuds utvecklingsteori
Freuds utvecklingsteori Biheviorizam ili bihejviorizam
Biheviorizam ili bihejviorizam Srednja kvadratna brzina molekula
Srednja kvadratna brzina molekula Pupinova teorija
Pupinova teorija Teorija x i y
Teorija x i y Funkcionalistička perspektiva
Funkcionalistička perspektiva Teorija sistema fon
Teorija sistema fon Teorija objektnih odnosa
Teorija objektnih odnosa Bihevioristička teorija učenja
Bihevioristička teorija učenja U teorija īsumā
U teorija īsumā Pijazeova teorija
Pijazeova teorija Zonska teorija
Zonska teorija Teorija i politika bilansa
Teorija i politika bilansa Moderna teorija organizacije
Moderna teorija organizacije Eriksonova teorija psihosocijalnog razvoja
Eriksonova teorija psihosocijalnog razvoja Teorija efikasnih nadnica
Teorija efikasnih nadnica Spirmanova teorija
Spirmanova teorija Trikotni prometni znaki
Trikotni prometni znaki Darvinas evoliucijos teorija
Darvinas evoliucijos teorija Teorija sistema fon
Teorija sistema fon Lombroza
Lombroza Teorija revizije
Teorija revizije Teorija situacijske prisile
Teorija situacijske prisile Multifaktorska teorija
Multifaktorska teorija Teorija ubikviteta
Teorija ubikviteta