MATLAB Tutorial ECE 002 Professor S Ahmadi Tutorial

MATLAB Tutorial ECE 002 Professor S. Ahmadi

Tutorial Outline • Functions using M-files. • Numerical Integration using the Trapezoidal Rule. • Example #1: Numerical Integration using Standard Programming (Slow). • Example #2: Numerical Integration using Vectorized MATLAB operations (Fast). • Student Lab Exercises.

What Are Function M-Files • Function M-files are user-defined subroutines that can be invoked in order to perform specific functions. • Input arguments are used to feed information to the function. • Output arguments store the results. • EX: a = sin(d). • All variables within the function are local, except outputs. NOTE: Local variables are variables that are only used within the function. They are not saved after the M-file executes.

Example of a Function M-File function answer = average 3(arg 1, arg 2, arg 3) % % % % A simple example about how MATLAB deals with user created functions in M-files. average 3 is a user-defined function. It could be named anything. average 3 takes the average of the three input parameters: arg 1, arg 2, arg 3 The output is stored in the variable answer and returned to the user. This M file must be saved as average 3. m answer = (arg 1+arg 2+arg 3)/3;

How to call a function in matlab X = sin(pi); % call the interior function of Matlab, sin Y % % % = input(“How are you? ”) call the interior function of Matlab, input is a function that requests information from the user during runtime Y=average 3(1, 2, 3); . % average 3 is a user-defined function. % The average value of 1, 2 and 3 will be stored in Y

Example: Calling a Function from within the Main program. % Example 1: This is a main program example to illustrate how functions are called. % input is a function that requests information from % the user during runtime. Var. A = input('What is the first number? '); Var. B = input('What is the second number? '); Var. C = input('What is the third number? '); Var. Average=average 3(Var. A, Var. B, Var. C); % num 2 str converts a number to a string. result=[‘The average value was’, num 2 str(Var. Average)]

Numerical Integration • General Approximation Made With Num. Integration: b n ∫ f(x) dx ≈ ∑ ci f(xi) a i=0 • Trapezoidal rule: • Integration finds the “Area” under a curve, between two points (a and b). • To approximate the area under a curve, use a familiar shape whose area we already know how to calculate easily. • In this case, we’ll use a trapezoid shape. • Area of trapezoid = ½ (b 1 + b 2) h y f(b) f(a) base 2 (b 1) x a b h base 2 (b 2)

Numerical Integration • Trapezoidal Rule (con’t): y • Area under curve ≈ Area of trapezoid under the curve f(b) f(a) • Area of trapezoid = ½ h [ b 1 + b 2 ] • Area under curve ≈ ½ (b-a) [ f(a) + f(b) ] x a b • Therefore, Trapezoidal Rule: b ∫ f(x) dx ≈ ½ (b-a) [ f(a) + f(b) ] a • How can we get a better approximation of the area under the curve? • Answer: Use More Trapezoids

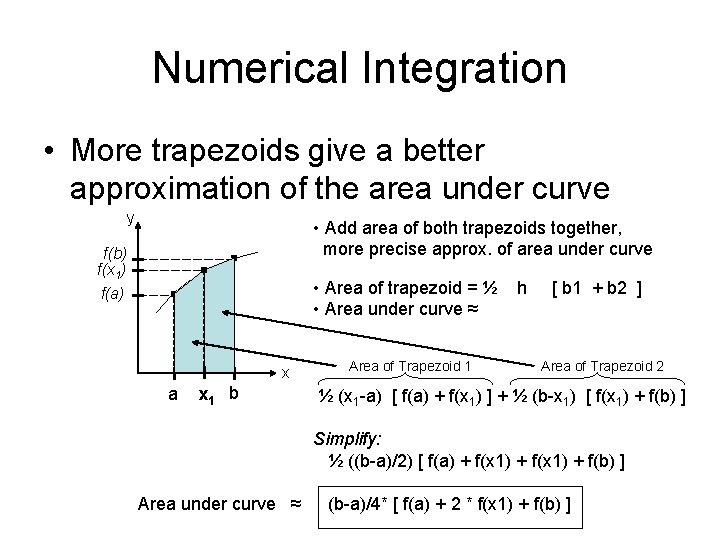
Numerical Integration • More trapezoids give a better approximation of the area under curve y • Add area of both trapezoids together, more precise approx. of area under curve f(b) f(x 1) • Area of trapezoid = ½ • Area under curve ≈ f(a) x a x 1 b Area of Trapezoid 1 h [ b 1 + b 2 ] Area of Trapezoid 2 ½ (x 1 -a) [ f(a) + f(x 1) ] + ½ (b-x 1) [ f(x 1) + f(b) ] Simplify: ½ ((b-a)/2) [ f(a) + f(x 1) + f(b) ] Area under curve ≈ (b-a)/4* [ f(a) + 2 * f(x 1) + f(b) ]

Numerical Integration • Using more trapezoids to approximate area under the curve is called: Composite Trapezoidal Rule • The more trapezoids, the better, so instead of two trapezoids, we’ll use n trapezoids. • The greater the value of n, the better our approximation of the area will be.

Composite Trapezoidal Rule • Divide interval [a, b] into n equally spaced subintervals (Add area of the n trapezoids) b x 1 x 2 b ∫ f(x) dx ≈ ∫ f(x) dx + … + ∫ f(x) dx a a x 1 xn-1 ≈ (b-a)/2 n [ f(a) + f(x 1) + f(x 2) +…+ f(xn-1) + f(b) ] ≈ (b-a)/2 n [ f(a) + 2 f(x 1) + 2 f(x 2) +…+ 2 f(xn-1) + f(b) ] b ∫ f(x) dx ≈ Δx/2 [ y 0 + 2 y 1 + 2 y 2 + … + 2 yn-1 + yn ] a Composite Trapezoidal Rule

Example 1 on Numerical Integration • Implementing Composite Trapezoidal Rule in Matlab • Example Curve: f(x) = 1/x , let’s integrate it from [e, 2 e] : 2 e 2 e e e ∫ 1/x dx = ln (x) | = ln (2 e) – ln (e) = ln (2) = 0. 6931 • Matlab Equivalent Area under curve: 1/x, from [e, 2 e] Inline(‘ 1/x’) function I=Trapez(f, a, b, n) % take f, add n trapezoids, from a to b % Integration using composite trapezoid rule h = (b-a)/n ; % increment s = feval(f, a) ; % starting value for i=1: n-1 x(i) = a + i*h ; In our case, input to the function will be: s = s+2 * feval (f, x(i)) ; f = inline (’ 1/x’) end a = e = 2. 7182818 s = s + feval(f, b) ; b = 2 e I = s*h/2 ;

Example 2 on Numerical Integration: Using MATLAB Vectorized Operations • This function carries out the same function as the previous example, but by using MATLAB Vectorized operations, it runs much faster. function I=Fast. Trap(f, a, b, n) % Same as the previous Trapezoidal function example, but using more % efficient MATLAB vectorized operations. h=(b-a)/n; s=feval(f, a); % Increment value % Starting value in=1: n-1; xpoints=a+in*h; % Defining the x-points ypoints=feval(vectorize(f), xpoints); % Get corresponding y-points sig=2*sum(ypoints); % Summing up values in ypoints, and mult. by 2 s=s+sig+feval(f, b); % Evaluating last term I=s*h/2;

Example 3: Integrating Trapezoidal/Fast. Trap Function into Main Program • Main program to test numerical integration function, and to measure difference in speed between the two previous functions. % Example 3: Main program to run the numerical integration function, % using the user-created Trapezoidal/Fast. Trap methods. fon=inline('log‘); a=exp(1); b=2*a; n=1000; % % Defines the function we wish to integrate. Starting point. Ending point. Number of intervals. tic % Start counter. Out. Value=Trapez (fon, a, b, n) % Calling Trapezoidal function. toc % Stop counter, and print out counters value. % Try replacing the Trapez function with the vectorized Fast. Trap % function, and notice the difference in speeds between the two.

Example 3: Continuation • Try two different values of N – N=1, 000 – N=100, 000. • For both N values, test the code using both functions for the Trapezoidal method: The normal Trapez Method, and the Fast. Trap Method. • Compare the difference in execution time between the standard way (Trapez), and the vectorized approach (Fast. Trap).

Additional MATLAB Exercise • Function: y(i) = sin [ x(i) ] • Where x(i) is “defined” by 101 uniformly spaced points in [0, 2π]. • Define the integral: x(i) Int (i) = ∫ sin (t) dt 0 • Calculate Int(i) for all values, i = 1, … , 101 • Plot y(i) and Int(i) versus x(i), for i =1, …, 101