Matlab Training Sessions 8 Introduction to Statistics Course

Matlab Training Sessions 8: Introduction to Statistics

Course Outline Weeks: 1. Introduction to Matlab and its Interface (Jan 13 2009) 2. Fundamentals (Operators) 3. Fundamentals (Flow) 4. Functions and M-Files 5. Importing Data 6. Plotting (2 D and 3 D) 7. Plotting (2 D and 3 D) 8. Statistical Tools in Matlab Additional classes will begin next week (Feb 10 2009) and will continue from where the first 8 sessions left off. These sessions will be run by Andrew Pruszynski (4 jap 1@qlink. queensu. ca) Course Website: http: //www. queensu. ca/neurosci/matlab. php

Week 8 Lecture Outline Basic Matlab Statistics A. Mean, Median, Variance B. Correlations B. Statistics Toolbox A. Parametric and Non-parametric statistical tests B. Curve fitting

Part A: Basics • The Matlab installation contains basic statistical tools. • Including, mean, median, standard deviation, error variance, and correlations • More advanced statistics are available from the statistics toolbox and include parametric and non -parametric comparisons, analysis of variance and curve fitting tools

Mean and Median Mean: Average or mean value of a distribution Median: Middle value of a sorted distribution M = mean(A), M = mean(A, dim), M = median(A) M = median(A, dim) M = mean(A), M = median(A): Returns the mean or median value of vector A. If A is a multidimensional mean/median returns an array of mean values. Example: A = [ 0 2 5 7 20] B = [1 2 3 336 468 4 7 7]; mean(A) = 6. 8 mean(B) = 3. 0000 4. 5000 6. 0000 (column-wise mean) mean(B, 2) = 2. 0000 4. 0000 6. 0000 (row-wise mean)
![Examples: A = [ 0 2 5 7 20] Mean and Median B = Examples: A = [ 0 2 5 7 20] Mean and Median B =](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-6.jpg)
Examples: A = [ 0 2 5 7 20] Mean and Median B = [1 2 3 336 468 4 7 7]; Mean: mean(A) = 6. 8 mean(B) = 3. 0 4. 5 6. 0 (column-wise mean) mean(B, 2) = 2. 0 4. 0 6. 0 (row-wise mean) Median: median(A) = 5 median(B) = 3. 5 4. 5 6. 5 (column-wise median) median(B, 2) = 2. 0 3. 0 6. 0 7. 0 (row-wise median)

Standard Deviation and Variance • • Standard deviation is calculated using the std() function std(X) : Calcuate the standard deviation of vector x If x is a matrix, std() will return the standard deviation of each column Variance (defined as the square of the standard deviation) is calculated using the var() function • var(X) : Calcuate the variance of vector x • If x is a matrix, var() will return the standard deviation of each column

Standard Error of the Mean • Often the most appropriate measure of error/variance is the standard error of the mean • Matlab does not contain a standard error function so it is useful to create your own. • The standard error of the mean is defined as the standard deviation divided by the square root of the number of samples

Standard Error of the Mean In Class Exercise 1: • Create a function called se that calculates the standard error of some vector supplied to the function Eg. se(x) should return the standard error of matrix x
![Standard Error of the Mean In Class Exercise 1: Solution function [result] = se(input_vect) Standard Error of the Mean In Class Exercise 1: Solution function [result] = se(input_vect)](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-10.jpg)
Standard Error of the Mean In Class Exercise 1: Solution function [result] = se(input_vect) result = STD(input_vect)/sqrt(length(input_vect)); return

In Class Exercise 2 • • 1. 2. 3. 4. From the class website download the file testdata 1. txt (http: //www. queensu. ca/neurosci/matlab. php) This text file contains data from two subjects arranged in columns Load the text file into matlab using any method you like (load, import, textread(), fscanf()) Calculate the mean and standard error for each subject In figure 1, plot the data distribution for each subject using the hist() plotting function In figure 2, plot the mean and standard error of each subject using a bar graph (bar() function and errorbar() functions).
![In Class Exercise 2 Solution %read data [subj 1, subj 2] = textread('testdata 1. In Class Exercise 2 Solution %read data [subj 1, subj 2] = textread('testdata 1.](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-12.jpg)
In Class Exercise 2 Solution %read data [subj 1, subj 2] = textread('testdata 1. txt', '%f%f', 'headerlines', 1) %plot distributions of each subject figure(1) hold on subplot(2, 1, 1) hist(subj 1) subplot(2, 1, 2) hist(subj 2) %plot mean and standard error on bar graph figure(2) hold on bar([1, 2], [mean(subj 1), mean(subj 2)]) errorbar([1, 2], [mean(subj 1), mean(subj 2)], [se(subj 1), se(subj 2)], 'r')

In Class Exercise 2 Solution Subject 1 Subject 2

Data Correlations • Matlab can calculate statistical correlations using the corrcoef() function • [R, P] = corrcoef(A, B) • Calculates a matrix of R correlation coefficiencts and P significance values (95% confidence intervals) for variables A and B R= A B Acor. A Bcor. A Acor. B Bcor. B

Data Correlations • Matlab can calculate statistical correlations using the corrcoef() function • [R, P] = corrcoef(A, B) • Calculates a matrix of R correlation coefficiencts and P significance values (95% confidence intervals) for variables A and B R= A B Acor. A Bcor. A Acor. B Bcor. B = 1 Bcor. A Acor. B 1

Data Correlations • Matlab can calculate statistical correlations using the corrcoef() function • [R, P] = corrcoef(A, B) • Calculates a matrix of R correlation coefficiencts and P significance values (95% confidence intervals) for variables A and B R= P= A B Acor. A Bcor. A Acor. B Bcor. B A B sig(Acor. A) sig(Bcor. A) sig(Acor. B) sig(Bcor. B) = 1 Bcor. A Acor. B 1 = 1 sig(Bcor. A) sig(Acor. B) 1
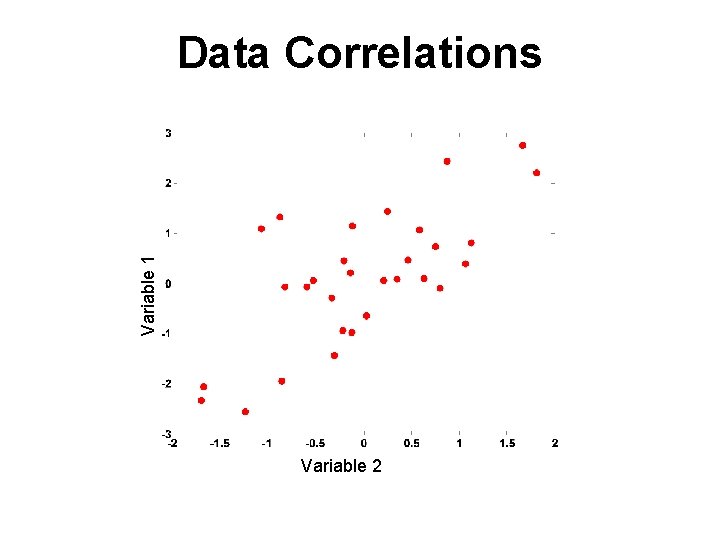
Variable 1 Data Correlations Variable 2
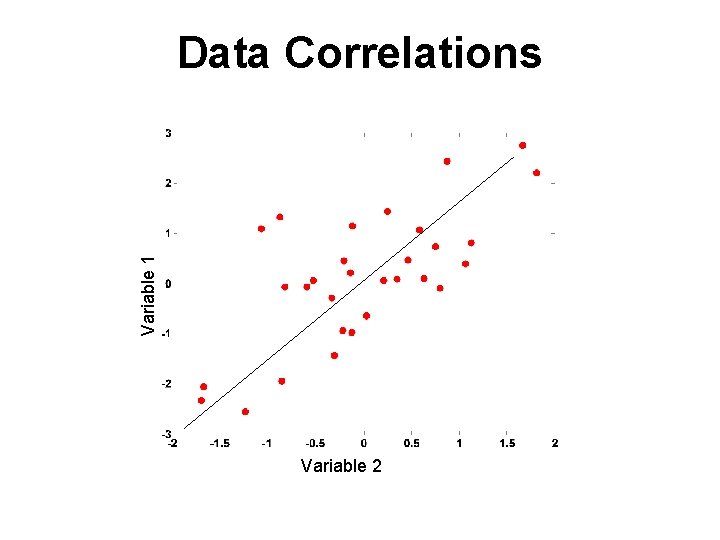
Variable 1 Data Correlations Variable 2
![Data Correlations % Compute sample correlation Variable 1 [r, p] = corrcoef([var 1, var Data Correlations % Compute sample correlation Variable 1 [r, p] = corrcoef([var 1, var](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-19.jpg)
Data Correlations % Compute sample correlation Variable 1 [r, p] = corrcoef([var 1, var 2]) Variable 2
![Data Correlations % Compute sample correlation Variable 1 [r, p] = corrcoef([var 1, var Data Correlations % Compute sample correlation Variable 1 [r, p] = corrcoef([var 1, var](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-20.jpg)
Data Correlations % Compute sample correlation Variable 1 [r, p] = corrcoef([var 1, var 2]) r = 1. 0000 0. 7051 1. 0000 p = 1. 0000 0. 0000 Variable 2 0. 0000 1. 0000

In Class Exercise 3 • From the class website download the file testdata 2. txt (http: //www. queensu. ca/neurosci/matlab. php) • This text file contains data from variables arranged in columns 1. Load the text file into matlab using any method you like (load, import, textread(), fscanf()) 2. Plot the data points 3. Calculate the Correlation
![In Class Exercise 3 Solution %read data [var 1, var 2] = textread('testdata 2. In Class Exercise 3 Solution %read data [var 1, var 2] = textread('testdata 2.](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-22.jpg)
In Class Exercise 3 Solution %read data [var 1, var 2] = textread('testdata 2. txt', '%f%f', 'headerlines', 1) % Plot data points figure(1) plot(var 1, var 2, 'ro') Variable 1 % Compute sample correlation [r] = corrcoef([var 1, var 2]) Variable 2

Part B: Statistics Toolbox • The Statistics tool box contains a large array of statistical tools. • This lecture will concentrate on some of the most commonly used statistics for research 1. Parametric and non-parametric comparisons 2. Curve Fitting

Comparison of Means • A wide variety of mathametical methods exist for determining whether the means of different groups are statistically different • Methods for comparing means can be either parametric (assumes data is normally distributed) or non-parametric (does not assume normal distribution)
![Parametric Tests - TTEST [H, P] = ttest 2(X, Y) Determines whether the means Parametric Tests - TTEST [H, P] = ttest 2(X, Y) Determines whether the means](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-25.jpg)
Parametric Tests - TTEST [H, P] = ttest 2(X, Y) Determines whether the means from matrices X and Y are statistically different. H return a 0 or 1 indicating accept or reject nul hypothesis (that the means are the same) P will return the significance level
![Parametric Tests - TTEST [H, P] = ttest 2(X, Y) Determines whether the means Parametric Tests - TTEST [H, P] = ttest 2(X, Y) Determines whether the means](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-26.jpg)
Parametric Tests - TTEST [H, P] = ttest 2(X, Y) Determines whether the means from matrices X and Y are statistically different. H return a 0 or 1 indicating accept or reject nul hypothesis (that the means are the same) P will return the significance level
![Example: For the data from exercise 3 [H, P] = ttest 2(var 1, var Example: For the data from exercise 3 [H, P] = ttest 2(var 1, var](http://slidetodoc.com/presentation_image_h2/746ecd522246a178cfa3c90854a7e304/image-27.jpg)
Example: For the data from exercise 3 [H, P] = ttest 2(var 1, var 2) >> [H, P] = ttest 2(var 1, var 2) H =1 P = 0. 00000014877 Variable 1 Parametric Tests - TTEST Variable 2

Non-Parametric Tests Ranksum • The wilcoxin ranksum test assesses whether the means of two groups are statistically different from each other. • This test is non-parametric and should be used when data is not normally distributed • Matlab implements the wilcoxin ranksum test using the ranksum() function ranksum(X, Y) statistically compares the means of two data distributions X and Y
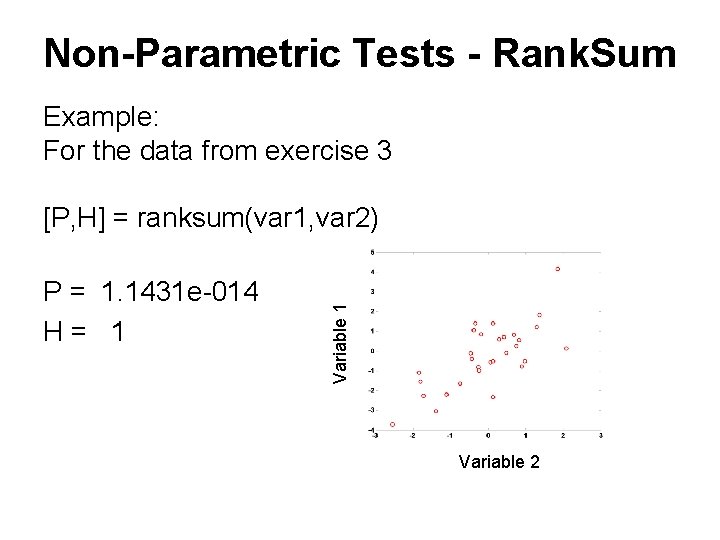
Non-Parametric Tests - Rank. Sum Example: For the data from exercise 3 P = 1. 1431 e-014 H= 1 Variable 1 [P, H] = ranksum(var 1, var 2) Variable 2
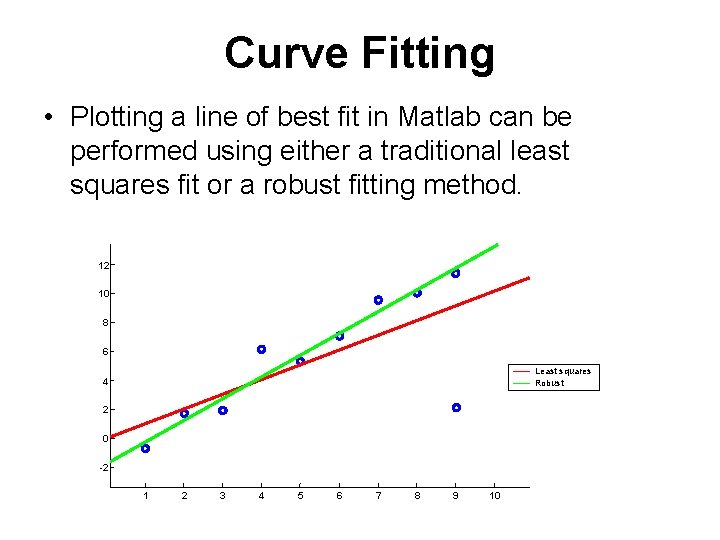
Curve Fitting • Plotting a line of best fit in Matlab can be performed using either a traditional least squares fit or a robust fitting method. 12 10 8 6 Least squares Robust 4 2 0 -2 1 2 3 4 5 6 7 8 9 10

Curve Fitting • A least squares linear fit minimizes the square of the distance between every data point and the line of best fit polyfit(X, Y, N) finds the coefficients of a polynomial P(X) of degree N that fits the data Uses least-square minimization N = 1 (linear fit) [P] = polyfit(X, Y, N) returns P, a matrix containing the slope and the x intercept for a linear fit [Y] = polyval(P, X) calculates the Y values for every X point on the line of best fit
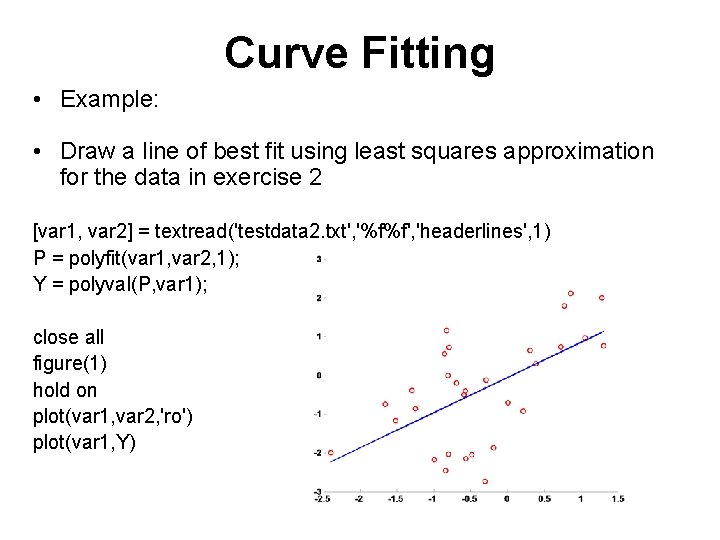
Curve Fitting • Example: • Draw a line of best fit using least squares approximation for the data in exercise 2 [var 1, var 2] = textread('testdata 2. txt', '%f%f', 'headerlines', 1) P = polyfit(var 1, var 2, 1); Y = polyval(P, var 1); close all figure(1) hold on plot(var 1, var 2, 'ro') plot(var 1, Y)

Curve Fitting • A least squares linear fit minimizes the square of the distance between every data point and the line of best fit • P = robustfit(X, Y) returns the vector B of the y intercept and slope, obtained by performing robust linear fit
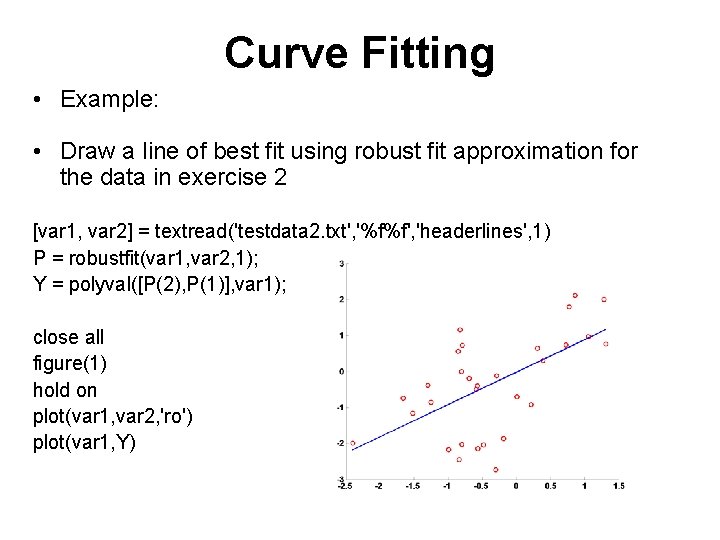
Curve Fitting • Example: • Draw a line of best fit using robust fit approximation for the data in exercise 2 [var 1, var 2] = textread('testdata 2. txt', '%f%f', 'headerlines', 1) P = robustfit(var 1, var 2, 1); Y = polyval([P(2), P(1)], var 1); close all figure(1) hold on plot(var 1, var 2, 'ro') plot(var 1, Y)

Ideas for Next Term? • Additional Statistics, ANOVAs ect. . • Curve fitting with quadratic functions and cubic splines • Algorithms and Data structures • Improving Program Execution Time • Assistance Tutorials for individual programming problems • Any Suggestions?

Getting Help and Documentation Digital 1. Accessible Help from the Matlab Start Menu 2. Updated online help from the Matlab Mathworks website: http: //www. mathworks. com/access/helpdesk/help/techdoc/matlab. html 3. Matlab command prompt function lookup 4. Built in Demo’s 5. Websites Hard Copy 3. Books, Guides, Reference The Student Edition of Matlab pub. Mathworks Inc.
- Slides: 36