Matlab Training Session 2 Matrix Operations and Relational

Matlab Training Session 2: Matrix Operations and Relational Operators

Course Outline Weeks: 1. Introduction to Matlab and its Interface (Jan 13 2009) 2. Fundamentals (Operators) 3. Fundamentals (Flow) 4. Importing Data 5. Functions and M-Files 6. Plotting (2 D and 3 D) 7. Statistical Tools in Matlab 8. Analysis and Data Structures Course Website: http: //www. queensu. ca/neurosci/matlab. php

Week 2 Lecture Outline Fundamentals of Matlab 1 A. Week 1 Review B. Matrix Operations: • • The empty matrix Creating multi-dimensional matrices Manipulating Matrices Matrix Operations C. Operators • Relational Operators

Week 1 Review Working with Matrices c = 5. 66 or c = [5. 66] x = [ 3. 5, 33. 22, 24. 5 ] x 1 = [ 2 5 3 -1] A=[1 2 4 2 -2 2 0 3 5 5 4 9] c is a scalar or a 1 x 1 matrix x is a row vector or a 1 x 3 matrix x 1 is column vector or a 4 x 1 matrix A is a 4 x 3 matrix

Week 1 Review Indexing Matrices • A m x n matrix is defined by the number of m rows and number of n columns • An individual element of a matrix can be specified with the notation A(i, j) or Ai, j for the generalized element, or by A(4, 1)=5 for a specific element. Example: >> A = [1 2 4 5; 6 3 8 2] A is a 2 x 4 matrix >> A(2, 1) Ans 6

Week 1 Review Indexing Matrices • Specific elements of any matrix can be overwritten using the matrix index Example: A = [1 2 4 5 6 3 8 2] >> A(2, 1) = 9 Ans A = [1 2 4 5 9 3 8 2]

Week 1 Review Indexing Matrices A = [1 2 4 5 6 3 8 2] • The colon operator can be used to index a range of elements >> A(1, 1: 3) Ans 1 2 4

Matrix Indexing Cont. . Indexing Matrices A = [1 2 4 5 6 3 8 2] • The colon operator can index all rows or columns without setting an explicit range >> A(: , 3) Ans 4 8 >> A(2, : ) Ans 6 3 8 2

B. Matrix Operations

Matrix Operations Indexing Matrices • An empty or null matrix can be created using square brackets >> A = [ ] ** TIP: The size and length functions can quickly return the number of elements and dimensions of a matrix variable

Matrix Operations Indexing Matrices A = [1 2 4 5 6 3 8 2] • The colon operator can be used to remove entire rows or columns >> A(: , 3) = [ ] A = [1 2 5 6 3 2] >> A(2, : ) = [ ] A = [1 2 5]

Matrix Operations Indexing Matrices A = [1 2 4 5 6 3 8 2] • However individual elements within a matrix cannot be assigned an empty value >> A(1, 3) = [ ] ? ? ? Subscripted assignment dimension mismatch.

N – Dimensional Matrices A = [1 2 4 5 6 3 8 2] B = [5 3 7 9 1 9 9 8] • Multidimensional matrices can be created by concatenating 2 -D matrices together • The cat function concatenates matrices of compatible dimensions together: Usage: cat(dimensions, Matrix 1, Matrix 2)

N – Dimensional Matrices Examples A = [1 2 4 5 6 3 8 2] B = [5 3 7 9 1 9 9 8] >> C = cat(3, [1, 2, 4, 5; 6, 3, 8, 2], [5, 3, 7, 9; 1, 9, 9, 8]) >> C = cat(3, A, B)

Matrix Operations Scalar Operations • Scalar (single value) calculations can be can performed on matrices and arrays Basic Calculation Operators + Addition - Subtraction * Multiplication / Division ^ Exponentiation

Matrix Operations Scalar Operations • Scalar (single value) calculations can be performed on matrices and arrays A = [1 2 4 5 6 3 8 2] B = [1 C = 5 7 3 3] Try: A + 10; A * 5; B / 2; A. ^C; A*B

Matrix Operations Scalar Operations • Scalar (single value) calculations can be performed on matrices and arrays A = [1 2 4 5 6 3 8 2] Try: A + 10 A*5 B/2 A^C B = [1 C = 5 7 3 3] What is happening here?

Matrix Operations • Matrix to matrix calculations can be performed on matrices and arrays Addition and Subtraction • Matrix dimensions must be the same or the added/subtracted value must be scalar A = [1 2 4 5 6 3 8 2] Try: >>A + B B = [1 C = 5 7 3 3] >>A + C >>A + D D = [2 4 6 8 1 3 5 7]

Matrix Operations Matrix Multiplication • Built in matrix multiplication in Matlab is either: 1. Algebraic dot product 2. Element by element multiplication

Matrix Operations The Dot Product • The dot product for two matrices A and B is defined whenever the number of columns of A are equal to the number of rows of b • A(x 1, y 1) * B(x 2, y 2)

Matrix Operations The Dot Product • The dot product for two matrices A and B is defined whenever the number of columns of A are equal to the number of rows of b • A(x 1, y 1) * B(x 2, y 2) = C(x 1, y 2)

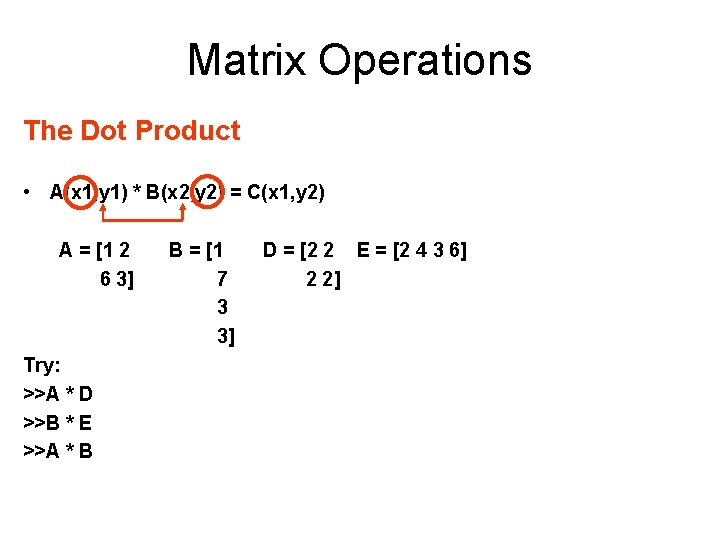
Matrix Operations The Dot Product • A(x 1, y 1) * B(x 2, y 2) = C(x 1, y 2) A = [1 2 6 3] Try: >>A * D >>B * E >>A * B B = [1 7 3 3] D = [2 2 E = [2 4 3 6] 2 2]

Matrix Operations Element by Element Multiplication • Element by element multiplication of matrices is performed with the. * operator • Matrices must have identical dimensions A = [1 2 63] >>A. * D Ans = [ 2 4 12 6] B = [1 7 3 3] D = [2 2 E = [2 4 3 6] 22]

Matrix Operations Matrix Division • Built in matrix division in Matlab is either: 1. Left or right matrix division 2. Element by element division

Matrix Operations Left and Right Division • Left and Right division utilizes the / and operators • Left () division: X = AB is a solution to A*X = B • Right (/) division: X = B/A is a solution to X*A = B • Left division requires A and B have the same number of rows • Right division requires A and B have the same number of columns

Matrix Operations Element by Element Division • Element by element division of matrices is performed with the. / operator • Matrices must have identical dimensions A = [1 2 4 5 6 3 8 2] B = [1 7 3 3] D = [2 2 E = [2 4 3 6] 2 2] >>A. / D Ans = [ 0. 5000 3. 0000 1. 5000 2. 0000 4. 0000 2. 5000 1. 0000 ]

Matrix Operations Element by Element Division • Any division by zero will be returned as a NAN in matlab (not a number) • Any subsequent operation with a NAN value will return NAN

Matrix Operations Matrix Exponents • Built in matrix Exponentiation in Matlab is either: 1. A series of Algebraic dot products 2. Element by element exponentiation Examples: • A^2 = A * A • A. ^2 = A. * A (Matrix must be square)

Matrix Operations Shortcut: Transposing Matrices • The transpose of a matrix is the matrix formed by interchanging the rows and columns of a given matrix A = [1 2 4 5 6 3 8 2] B = [1 7 3 3] >> transpose(A) A = [1 6 23 48 5 2] >> B’ B = [1 7 3 3]

Matrix Operations Other handy built in matrix functions Include: inv() det() poly() kron() Matrix inverse Matrix determinant Characteristic Polynomial Kronecker tensor product

C. Relational Operators

Relational Operators • Relational operators are used to compare two scaler values or matrices of equal dimensions Relational Operators < less than <= less than or equal to > Greater than >= Greater than or equal to == equal ~= not equal

Relational Operators • Comparison occurs between pairs of corresponding elements • A 1 or 0 is returned for each comparison indicating TRUE or FALSE • Matrix dimensions must be equal! >> 5 == 5 Ans 1 >> 20 >= 15 Ans 1

Relational Operators A = [1 2 4 5 6 3 8 2] Try: >>A > B >> A < C B=7 C = [2 2 2 2 2]

Relational Operators The Find Function • The ‘find’ function is extremely helpful with relational operators for finding all matrix elements that fit some criteria A = [1 2 4 5 B=7 C = [2 2 D = [0 2 0 5 0 2] 6 3 8 2] 2 2] • The positions of all elements that fit the given criteria are returned >> find(D > 0) • The resultant positions can be used as indexes to change these elements >> D(find(D>0)) = 10 D = [10 2 10 5 10 2]

Relational Operators The Find Function A = [1 2 4 5 6 3 8 2] B=7 C = [2 2 2 2 2] D = [0 2 0 5 0 2] • The ‘find’ function can also return the row and column indexes of of matching elements by specifying row and column arguments >> [x, y] = find(A == 5) • The matching elements will be indexed by (x 1, y 1), (x 2, y 2), … >> A(x, y) = 10 A = [ 1 2 4 10 6382 ]

Getting Help and Documentation Digital 1. Accessible Help from the Matlab Start Menu 2. Updated online help from the Matlab Mathworks website: http: //www. mathworks. com/access/helpdesk/help/techdoc/matlab. html 3. Matlab command prompt function lookup 4. Built in Demo’s 5. Websites Hard Copy 3. Books, Guides, Reference The Student Edition of Matlab pub. Mathworks Inc.